Аксонометрический чертеж что это

Аксонометрический чертеж

Проектные объекты с разной композиционной и пластической структурами целесообразно изображать в наиболее выигрышной для каждого из них графической технике. В некоторых случаях для этих целей предпочтительны аксонометрические чертежи. Аксонометрическое черчение – условное изображение предмета в аксонометрии, само понятие которой возникло из словосочетания “аксон” (ось) и “метрео” (измеряю) – термины, взятые из древнегреческого языка. Метод аксонометрического проецирования есть ракурсное изображение предмета, параллельно спроецированное на изобразительную плоскость под определенным к ней углом (рис. 6). Аксонометрический чертеж – средство позволяющее получить при взгляде на объект в ракурсе с верхней или нижней точек зрения наиболее полное впечатление об его объемных и пространственных характеристиках.

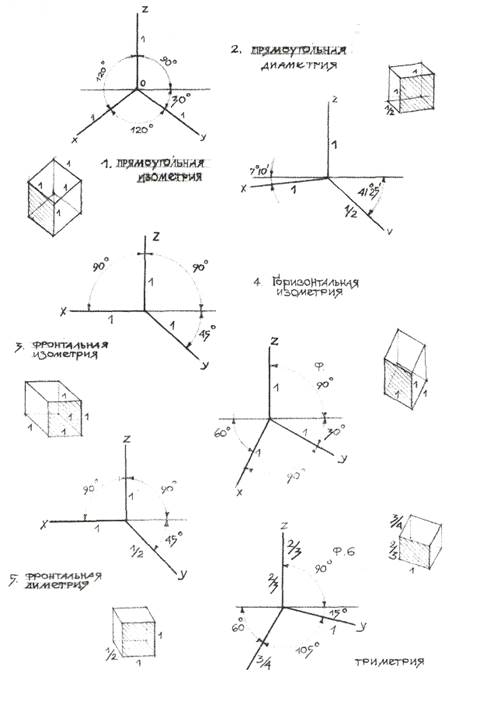
Виды аксонометрических изображений.В нашей стране виды аксонометрических проекций классифицируются и подчиняются ГОСТам. Обращаем внимание, что изображенные на рис. 6 аксонометрические чертежи сориентированы по трем осям, среди которых вертикальная ось обозначена z, левая от вертикали ось обозначена x, правая от вертикали ось обозначена y. Вдоль осей аксонометрических фигур нанесены цифровые обозначения пропорционального сокращения (искажения) граней изображаемых фигур, именуемые в тексте “индекс искажения”: 1 – ось или грань фигуры с таким индексом не сокращается, имеет линейные пропорции 1 : 1; 3/4 – ось или грань фигуры с таким индексом сокращается в пропорциях 3 : 4; 2/3 – ось или грань фигуры с таким индексом сокращается в пропорциях 2 : 3; 1/2 – в направлении данной оси или грани фигуры изображения сокращаются в пропорциях 1 : 2.

Рис. 6. Схемы построения аксонометрии по ГОСТу.

В реальном или учебном проектировании согласно ГОСТ 2.317–69 аксонометрические проекции подразделяются на прямоугольные и косоугольные аксонометрические проекции.

Прямоугольные, где проецирующие лучи перпендикулярны картинной плоскости. Прямоугольные проекции делятся на:

— прямоугольную изометрическую проекцию, где углы между осями z, x, y равны 120°, а углы между горизонтальной прямой и осями x и y равны 30°, где изображение по всем трем осям не сокращается и обозначается индексом сокращения 1 (рис. 6, 1);

— прямоугольную диметрическую проекцию, где ось x направлена к горизонтальной прямой под углом 7° 10′, ось y направлена к горизонтальной прямой под углом 41°25′. Индекс сокращения изображения по осям z, и x равен 1, а индекс сокращения по оси y равен 1/2 (рис. 6, 2);

Косоугольные проекции, где проецирующие лучи наклонны к картинной плоскости. Косоугольные проекции в свою очередь делятся на:

— фронтальную изометрическую проекцию, где угол между осями z и x равен 90°, а угол оси y к горизонталь­ной прямой равен 45°. Индексы сокра­щения по всем трем осям z, x, y равен 1 (рис. 6, 3);

— горизонтальную изометрическую проекцию, где угол, под которым ось x встречается с горизонтальной прямой, равен 60°, а угол встречи оси y с гори­зонтальной прямой 30°. Индекс сокра­щения по всем трем осям z, x, y равен 1 (рис. 6, 4);

— фронтальную диметрическую проекцию, где угол между осями z и x равен 90°, а ось y встречается с горизон­тальной прямой под углом в 45°. Индекс искажения по осям z и x равен 1, а ин­декс искажения по оси Y равен 1/2 (рис. 6, 5);

— триметрическая проекция отличается разными показателями индекса искажения по всем трем осям. С горизонтальной прямой ось x встречается под углом 60°, ось y под углом 15°, между осями x и y угол равен 105°. Количе­ственные показатели индексом искаже­ния по трем осям в определенных преде­лах могут меняться. На рис. 6, 6 показа­тели искажения по оси z равны 2/3, по оси x – 3/4, а по оси y – 1.

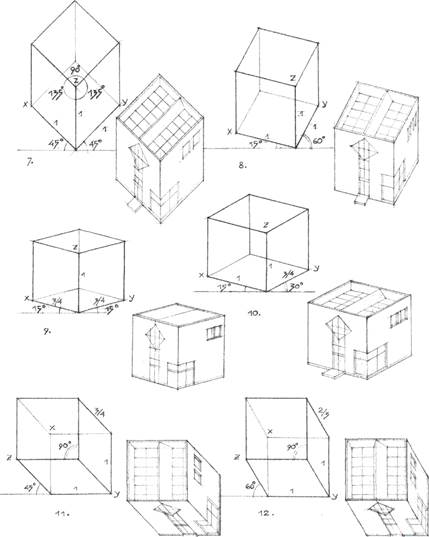
Фигуры 7, 8, 9, 10, 11, 12 на рис. 7 демонстрируют широко употребляемые в США приемы аксонометрических изображений. Представленные приемы существенно отличаются от аксонометрических изображений по российскому ГОСТу и представляют определенный интерес ракурсных изображений проектируемых объектов.

При исполнении всех видов аксонометрических чертежей не следует:

— использовать аксонометрические чертежи без строгой ориентации чертежных проекций относительно вертикальной и горизонтальной осей картинной плоскости чертежа;

Рис. 7. Построение нетрадиционных схем аксонометрии

— грани аксонометрических проекций следует чертить, строго соблюдая параллельность прямых;

— не следует произвольно подбирать пропорции искажения по трем осям аксонометрии, пропорциональное искажения граней аксонометрического изображения должно быть исключительно точным;

— при изображении объектов с планами цилиндрическими или близкими к квадрату не следует использовать приемы аксонометрии, изображенные на рис. 6. (1, 3).

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник

Большая Энциклопедия Нефти и Газа

Аксонометрический чертеж

Аксонометрический чертеж состоит только из одной параллельной проекции данного объекта, дополненной проекцией пространственной системы координат, к которой предварительно отнесен изображаемый объект. [3]

Аксонометрические чертежи применяют в различных областях промышленности и при их зрительном воприятии наибольшую роль также играет информационный аспект. Алгоритмы построения аксонометрии позволяют изменять проецирующий аппарат. При неудачном выборе последнего вырождение инциденций может привести к неполноте аксонометрического чертежа и к потере возможности использовать этот чертеж как орудие исследования. Изложенное позволяет сделать вывод, что невырожденность инциденций оригинала на аксонометрическом чертеже является одним из критериев его оптимальности. [4]

Только аксонометрический чертеж прямой, параллельной координатной плоскости IIj ( Oxy), имеет отличительную особенность: аксонометрическая и вторичная проекции прямой всегда параллельны. Сказанное справедливо и для чертежей прямых, параллельных координатным плоскостям II2 ( O. [8]

Такой аксонометрический чертеж называют приведенным. [9]

Рассмотрим аксонометрический чертеж прямой г, параллельной направлению проектирования. [10]

Получим аксонометрический чертеж точки А. [11]

Масштабы ортогонального и аксонометрического чертежа могут быть различными. [12]

На аксонометрическом чертеже ( рис. 437 6) дуги круга преобразовались в дуги эллипса, также плавно сопрягающиеся в точках А, В, С, D, Е между собой и с прямыми линиями. [13]

На аксонометрическом чертеже могут быть нанесены размеры, обеспечивающие его обратимость. В этом случае отпадает необходимость в указании показателей искажения по осям. [14]

На аксонометрических чертежах прямые, перпендикулярные и аксонометрической плоскости проекций ГГ ( на рис. 2.4 прямая т) и координатной плоскости IIj ( Oxy) ( на рис. 2.4 прямая п), называются проецирующими. Аксонометрическая и вторичная проекции прямых, перпендикулярных координатным плоскостям П2 ( СЬсг), П3 ( О. [15]

Источник

Статьи о радиотехнике, технологиях, чертежах, 3D-моделировании

Публикации для людей, интересующихся наукой и техникой

Мысленное воспроизведение формы и размеров сложной детали, изделия, сборочной единицы не всегда достигается по проекционному чертежу. В этом случае на помощь проекционному чертежу приходят аксонометрические проекции, т.е. изображения, на которых деталь, изделие, сборочная единица воспринимаются наглядно, объемно.

Известно, что предметы окружающего нас мира являются трехмерными, имея некоторые размеры по высоте, длине, ширине. При построении ортогонального проекционного изображения одно из измерений всегда вырождается, поскольку направление проецирования совпадает с одним из направлений мерности. Поэтому ортогональный проекционный чертеж позволяет судить о двух измерениях.

Кроме того, плоские контуры, изображаемых в проекционном чертеже геометрических образов, часто выглядят отрезками прямых, что также затрудняет мысленное воспроизведение формы. Аксонометрические проекции лишены этого недостатка, ибо геометрический образ проецируется на плоскость так, что ни одно из измерений не вырождается в точку и изображение дает все три измерения (высоту, длину, ширину), что приводит к объемному восприятию. Объемное изображение в большей степени передает информацию о форме и пропорциях детали, изделия, сборочной единицы, нежели проекционный чертеж.

Аксонометрические проекции не заменяют проекционного чертежа, а только его дополняют. Аксонометрия – не самоцель, её построение весьма сложно, и она требуется лишь тогда, когда по проекционному чертежу весьма трудно представить форму изображенного геометрического образа.

При выполнении рабочих чертежей деталей, вопрос о необходимости исполнения той или иной детали в аксонометрии решается ведущим преподавателем. При конструировании же новых деталей машин и механизмов аксонометрические проекции используются обязательно.

Вполне очевидно, что умение правильно выбрать вид аксонометрии, знать различные приемы построения в аксонометрии и, наконец, обладать навыками построения деталей машин и механизмов в аксонометрии совершенно необходимы будущему инженеру.

Очень часто в практике проецирования, наряду с изображением предмета в системе ортогональных проекций, возникает необходимость наглядных видов.

Для построения таких изображений применяют проекции, которые называют аксонометрическими, что означает «аксон» – ось, «метрео» – измерение. В современном проектировании они широко применяются и используются потому, что обладают большой наглядностью, сравнительно простым построением.

Аксонометрия поможет лучше понять форму конструкций, их взаимодействие, а также общую форму здания и его внешний вид. Поэтому любой грамотный инженер–конструктор должен хорошо владеть техникой построения аксонометрии и уметь пользоваться ею.

Аксонометрический чертеж только тогда будет обратимым, если для любой точки изображенного на нем объекта можно построить ее основание (вторичную проекцию). Плоскость, на которую проецируется заданный объект, называется аксонометрической плоскостью проекций. Плоскость проекций можно выбирать вполне произвольно. Направление проецирования также выбирается произвольно. Например, мы можем проецировать заданный объект лучами, перпендикулярными к выбранной плоскости проекций. В этом случае аксонометрия называется ортогональной.

Если проецирующие лучи наклонены к плоскости проекций под произвольным углом, то такая аксонометрия называется косоугольной. Чтобы получить наглядное аксонометрическое изображение некоторого геометрического образа, прежде всего, его нужно «привязать» к системе декартовых осей координат, затем выбрать направление проецирования, отличное от направления любой из декартовых осей и параллельно этому направлению спроецировать геометрический образ на картинную плоскость. Полученное таким образом параллельное изображение геометрического образа будет его аксонометрической проекцией. Грани геометрического образа, параллельные плоскостям проекций, в аксонометрической проекции не будут вырождаться в отрезки прямых. Следует отметить, что в общем случае происходят искажения как угловых величин геометрического образа (в том числе и декартовых углов), так и его линейных размеров. Однако эти искажения не мешают объемному восприятию, а, наоборот, ему способствуют. Таким образом, сутью аксонометрических проекций является построение параллельной проекции геометрического образа на плоскость, когда направление проецирования не совпадает ни с одной из декартовых осей координат.

ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ

Аксонометрические проекции называют прямоугольными если направление проецирования и проецирующие прямые перпендикулярны плоскости, на которую они проецируются, и косоугольными если направление проецирования не перпендикулярно плоскости аксонометрических проекций. Проекции аксонометрических осей на плоскость называют аксонометрическими осями, а проекции единицы измерения по осям – аксонометрическими единицами измерения.

В зависимости от положения предмета и осей координат относительно плоскости проекций, а также в зависимости от направления проецирования единицы измерения проецируются в общем случае с искажением. Искажаются и размеры проецируемых предметов. Отношение длины аксонометрической единицы к ее истинной величине называют показателем или коэффициентом искажения для данной оси координат.

Аксонометрические проекции называют изометрическими, если коэффициенты искажения по всем осям равны; ди метрическими, если коэффициенты искажения по двум осям равны и триметрическими, если все коэффициенты различны. Для аксонометрических изображений предметов применяют пять видов аксонометрических проекций: прямоугольные – изометрические и ди метрические, косоугольные – фронтальные ди метрические, фронтальные изометрически и горизонтальные изометрические.

ХАРАКТЕРНЫЕ ПОСТРОЕНИЯ В АКСОНОМЕТРИИ

Реальные детали машин и механизмов представляют собой, как правило, комбинации и сочетания различных геометрических образов, которые при взаимном пересечении образуют линии перехода. Эти линии могут быть как пространственными, так и плоскими. Умение строить эти линии в аксонометрии является совершенно необходимым, ибо в противном случае нельзя правильно передать форму изображаемой детали. Чтобы построить наглядное изображение линии перехода двух геометрических образов, прежде всего необходимо построить проекции этой линии. Общие точки искомой линии находятся, как правило, с помощью вспомогательных секущих плоскостей, чаще всего – плоскостей уровня. Разумеется, что секущие плоскости нужно выбрать так, чтобы они пересекали конкурирующие поверхности по простейшим линиям (прямым или окружностям).

Известно, что линии среза получаются в результате пересечения поверхности вращения плоскостью (или плоскостями), параллельно оси поверхности. При построении этой линии, нужно учитывать следующее обстоятельство. Если поверхность является закономерной, то и линии «среза» также являются закономерными, если поверхность вращения случайной формы, то линия «среза» незакономерная. Например, линия «среза» для конуса вращения является гиперболой, для цилиндра вращения – образующими для – сферы окружностью.

В рассматриваемом примере линии среза в пространстве являются гиперболами, аксонометрические проекции которых тоже являются гиперболами.

Следовательно, чтобы правильно построить аксонометрическую проекцию линии «среза», лежащей, допустим, во фронтальной плоскости, нужно построить гиперболу в аксонометрии. В практике машиностроительного черчения допускается заменять линии «среза» граней гайки (болта), являющихся в действительности гиперболами дугами окружности, что упрощает построения, ибо каждую из условных дуг можно провести через три соответствующие точки. Аксонометрические проекции этих дуг являются частями эллипсов.

Во всех остальных случаях, аксонометрическая проекция линии среза строится с помощью дополнительных сечений, а если поверхность вращения является линейчатой – с помощью образующих.

Пусть прямой круговой конус пересекается фронтальной плоскостью. Линия среза представляет собой гиперболу, ее аксонометрическая проекция может быть построена с помощью горизонтальных секущих плоскостей и с помощью образующих. В рассматриваемом примере для построения точек линии «среза» удобнее пользоваться образующими конуса.

Получить консультацию или заказать выполнение задания по аксонометрическим и изометрическим проекциям можно здесь.

ВИД ПРАВИЛЬНЫХ И НЕПРАВИЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ТЕЛ В АКСОНОМЕТРИИ

Геометрические образы правильной формы (многогранники и поверхности вращения – прямой круговой цилиндр, прямой круговой конус, сфера, правильные призмы и пирамиды) часто встречаются в реальных деталях машин и механизмов. Правильные геометрические тела характеризуется наличием в них различных осей и плоскостей симметрии, что позволяет строить аксонометрические изображения этих тел по принципу симметрии.

Допустим, требуется построить аксонометрическое изображение прямой шестигранной пирамиды. Прежде всего отнесем рассматриваемый геометрический образ к системе прямоугольных координат, выбрав положение осей так, чтобы они лежали в соответствующих плоскостях симметрии. При таком положении осей видно, что элементы геометрического образа располагаются симметрично относительно плоскостей Р и Q и, следовательно, относительно осей ОХ и ОУ. Строим аксонометрические оси (например, для ортогональной изометрии) и на этих осях откладываем точки 1, 4 по оси OX и a, b по оси OY.

На горизонтальной проекции геометрического образа эти точки располагаются симметрично относительно осей ОХ и ОY (или относительно начало осей точки О). Следовательно, в аксонометрии они располагаются таким же образом.

Строим стороны основания 23 и 56, которые параллельны оси ОХ, так как их проекции параллельны этой же оси. Найдя аксонометрическое положение вершины S, строим полную аксонометрическую проекцию данного геометрического образа.

Принцип симметрии используется для построения наглядных изображений любых правильных многогранников Построение наглядных изображений правильных поверхностей вращения несколько отлично от рассмотренного, т.к. в основе этих поверхностей лежат окружности, аксонометрические проекции которых изображаются эллипсами.

ПРИМЕР ВЫПОЛНЕНИЯ ДЕТАЛИ «ВЕНТИЛЬ» В АКСОНОМЕТРИИ

Выполнение деталей в аксонометрии поясним на примере выполнения корпуса вентиля. Даны вертикальная и горизонтальная проекции детали. Построение аксонометрического изображения начинаем с выбора вида аксонометрической проекции. Для данного геометрического образа удобнее использовать изометрию, так как все окружности, лежащие в различных плоскостях, будут изображаться одинаковыми по форме эллипсами. Построение начинаем с вычерчивания осей Х, Y, Z. По оси Х симметрично точке О1 откладываем отрезок 12, который соответствует длине корпуса, т.е. определяем положение левого и правого торцов боковых фланцев. Из начала координат проводим окружность, радиус которой равен 1,22 радиуса центральной внешней сферы корпуса, а по оси Z – расстояние 03′, это будет центр верхнего торца корпуса, проецирующего тоже в эллипс, большая ось которого будет перпендикулярна оси Z₁.

Далее и соответственно по оси Х₁ и Z₁ строим внутренние торцы фланцев, с помощью отрезков 14, 25, 36 находим центры искомых эллипсов. И, наконец, пристраиваем цилиндрические патрубки фланцев, примыкающие к сферической части корпуса. Изображаемая деталь требует построения разреза в аксонометрии, который может быть выполнен двумя парами секущих плоскостей: 1-ая пара – фронтальная и профильная плоскости, 2-ая пара – фронтальная и горизонтальная плоскости. Остановимся на первом варианте (введем плоскости S₁ и S₂).

Плоскость S₁ пересекает цилиндрические поверхности фланцев и патрубков по образующим АВ и CD…, а сферическую поверхность по окружностям (эллипсам). Плоскость S₂ пересекает сферическую поверхность также по окружностям (эллипсам), а вертикальный патрубок и горизонтальный фланец по образующим.

Источник