Авл дерево что это

Реализации алгоритмов/АВЛ-дерево

АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

Содержание

Общие свойства [ править ]

Тип дерева можно описать так

AVL-условия можно проверить так

Балансировка [ править ]

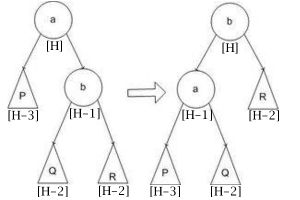
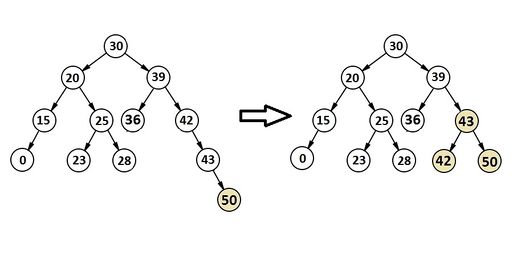
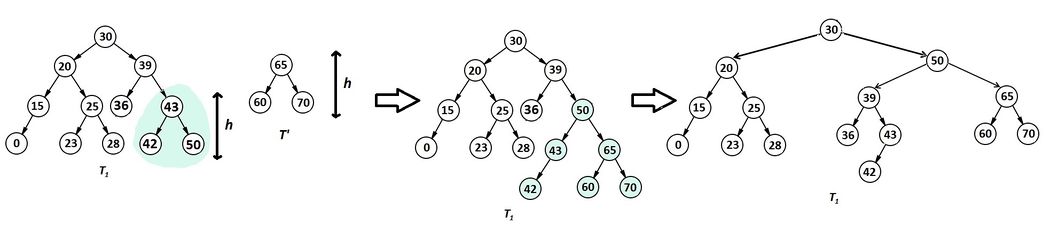
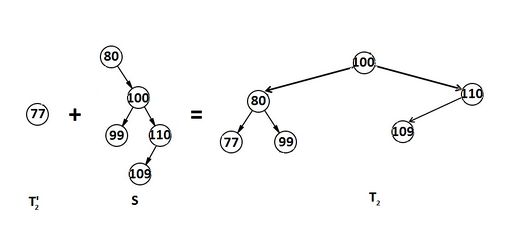
Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится высота R.

Данное вращение используется тогда, когда (высота b-поддерева — высота R) = 2 и высота С высота L.

В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться.

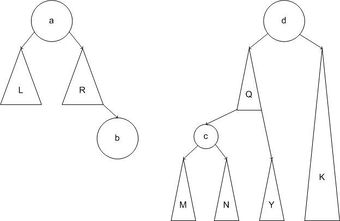
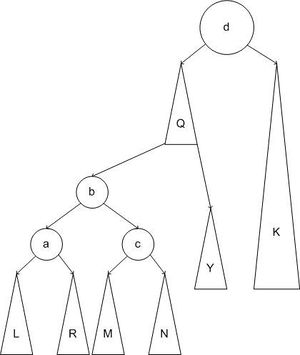
Также можно заметить, что большое вращение это комбинация правого и левого малого вращения.

Из-за условия балансированности высота дерева О(log(N)), где N- количество вершин, поэтому добавление элемента требует O(log(N)) операций.

Алгоритм добавления вершины [ править ]

Показатель сбалансированности в дальнейшем будем интерпретировать как разность между высотой левого и правого поддерева, а алгоритм будет основаться на типе TAVLTree, описанном выше. Непосредственно при вставке (листу) присваивается нулевой баланс. Процесс включения вершины состоит из трех частей (данный процесс описан Николасом Виртом в «Алгоритмы и структуры данных»):

Будем возвращать в качестве результата функции, уменьшилась высота дерева или нет. Предположим, что процесс из левой ветви возвращается к родителю (рекурсия идет назад), тогда возможны три случая: < h_l — высота левого поддерева, h_r — высота правого поддерева > Включение вершины в левое поддерево приведет к

В третьей ситуации требуется определить балансировку левого поддерева. Если левое поддерево этой вершины (Tree^.left^.left) выше правого (Tree^.left^.right), то требуется большое правое вращение, иначе хватит малого правого. Аналогичные (симметричные) рассуждения можно привести и для включение в правое поддерево.

вспомогательная функция сравнивающая два ключа

Рекурсивная процедура вставки:

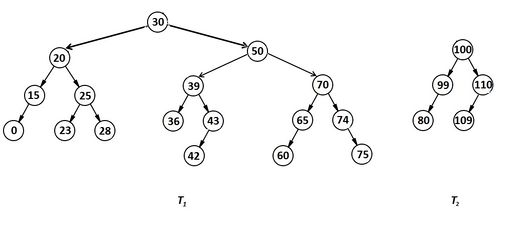
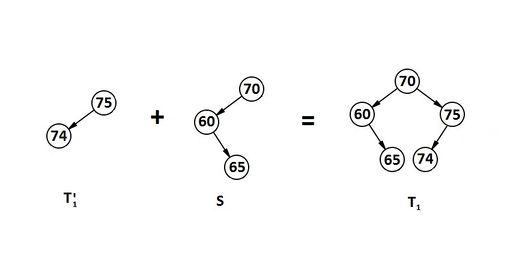
Алгоритм удаления вершины [ править ]

Для простоты опишем рекурсивный алгоритм удаления. Если вершина — лист, то удалим её и вызовем балансировку всех её предков в порядке от родителя к корню. Иначе найдём самую близкую по значению вершину в поддереве наибольшей высоты (правом или левом) и переместим её на место удаляемой вершины, при этом вызвав процедуру её удаления.

Упрощённый вариант удаления можно описать таким образом

Докажем, что данный алгоритм сохраняет балансировку. Для этого докажем по индукции по высоте дерева, что после удаления некоторой вершины из дерева и последующей балансировки высота дерева уменьшается не более, чем на 1. База индукции: Для листа очевидно верно. Шаг индукции: Либо условие балансированности в корне (после удаления корень может изменится) не нарушилось, тогда высота данного дерева не изменилась, либо уменьшилось строго меньшее из поддеревьев => высота до балансировки не изменилась => после уменьшится не более чем на 1.

Очевидно, что в результате указанных действий процедура удаления вызывается не более 3 раз, так как у вершины, удаляемой по второму вызову, нет одного из поддеревьев. Но поиск ближайшего каждый раз требует O(N) операций. Становится очевидной возможность оптимизации: поиск ближайшей вершины может быть выполнен по краю поддерева, что сокращает сложность до O(log(N)).

Нерекурсивная вставка в АВЛ-дерево сверху-вниз [ править ]

Нерекурсивный алгоритм сложнее рекурсивного.

Нерекурсивное удаление из АВЛ-дерева сверху вниз [ править ]

Для реализации удаления будем исходить из того же принципа, что и при вставке: найдём вершину, удаление из которой не приведёт к изменению её высоты. Существует два случая:

Для облегчения понимания приведённый алгоритм не содержит каких-либо оптимизаций. В отличие от рекурсивного алгоритма, найденная удаляемая вершина заменяется значением из левой подветви. Этот алгоритм можно оптимизировать так же, как и рекурсивный (за счёт того, что после нахождения удаляемой вершины известно направление движения):

Источник

АВЛ-дерево.

АВЛ-дерево – структура данных, изобретенная в 1968 году двумя советскими математиками: Евгением Михайловичем Ландисом и Георгием Максимовичем Адельсон-Вельским. Прежде чем дать конструктивное определение АВЛ-дереву, сделаем это для сбалансированного двоичного дерева поиска.

Сбалансированным называется такое двоичное дерево поиска, в котором высота каждого из поддеревьев, имеющих общий корень, отличается не более чем на некоторую константу k, и при этом выполняются условия характерные для двоичного дерева поиска.

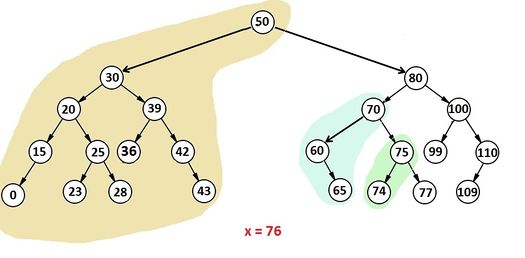
АВЛ-дерево – сбалансированное двоичное дерево поиска с k=1. Для его узлов определен коэффициент сбалансированности (balance factor). Balance factor – это разность высот правого и левого поддеревьев, принимающая одно значение из множества <-1, 0, 1>. Ниже изображен пример АВЛ-дерева, каждому узлу которого поставлен в соответствие его реальный коэффициент сбалансированности.

Пример АВЛ-дерева

Положим B_i – коэффициент сбалансированности узла T_i (i – номер узла, отсчитываемый сверху вниз от корневого узла по уровням слева направо). Balance factor узла T_i рассчитывается следующим образом. Пусть функция h() с параметрами T_iи L возвращает высоту левого поддерева L узла T_i, а с T_i и R – правого. Тогда B_i=h(T_i, R)-h(T_i, L). Например, B₄=-1, так как h(T₄, R)-h(T₄, L)=0-1=-1.

Сбалансированное дерево эффективно в обработке, что следует из следующих рассуждений. Максимальное количество шагов, которое может потребоваться для обнаружения нужного узла, равно количеству уровней самого бинарного дерева поиска. А так как поддеревья сбалансированного дерева, «растущие» из произвольного корня, практически симметричны, то и его листья расположены на сравнительно невысоком уровне, т. е. высота дерева сводиться к оптимальному минимуму. Поэтому критерий баланса положительно сказывается на общей производительности. Но в процессе обработки АВЛ-дерева, балансировка может нарушиться, тогда потребуется осуществить операцию балансировки. Помимо нее, над АВЛ-деревом определены операции вставки и удаления элемента. Именно выполнение последних может привести к дисбалансу дерева.

Доказано, что высота АВЛ-дерева, имеющего N узлов, примерно равна log₂N. Беря в виду это, а также то, то, что время выполнения операций добавления и удаления напрямую зависит от операции поиска, получим временную сложность трех операций для худшего и среднего случая – O(logN).

Прежде чем рассматривать основные операции над АВЛ-деревом, определим структуру для представления его узлов, а также три специальные функции:

Источник

АВЛ-дерево

АВЛ-дерево (англ. AVL-Tree) — сбалансированное двоичное дерево поиска, в котором поддерживается следующее свойство: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962 году.

Содержание

Высота дерева [ править ]

Допустим [math]m_h = F_ — 1[/math] — верно.

Таким образом, равенство [math]m_h = F_ — 1[/math] — доказано.[math]\triangleleft[/math]

[math]n \geqslant \varphi^[/math]

[math]\log_<\varphi>n \geqslant h[/math]

Балансировка [ править ]

Для балансировки вершины используются один из 4 типов вращений:

[math]diff[a] = 0[/math] и [math]diff[b] = 0[/math]

Малый левый поворот:

Большой левый поворот пишется проще:

Малое правое и большое правое вращение определяются симметрично малому левому и большому левому вращению. В каждом случае операция приводит к нужному результату, а полная высота уменьшается не более чем на [math]1[/math] и не может увеличиться.

Все вращения, очевидно, требуют [math]O(1)[/math] операций.

Операции [ править ]

Добавление вершины [ править ]

Так как в процессе добавления вершины мы рассматриваем не более, чем [math] O(h) [/math] вершин дерева, и для каждой запускаем балансировку не более одного раза, то суммарное количество операций при включении новой вершины в дерево составляет [math] O(\log) [/math] операций.

Удаление вершины [ править ]

Поиск вершины, минимум/максимум в дереве, etc. [ править ]

Остальные операции не меняют структуры дерева, поэтому выполняются так же, как и в наивной реализации дерева поиска.

Слияние двух AVL-деревьев [ править ]

Дерево [math]T_1[/math] и [math]T_2[/math] до слияния

Дерево [math]T_2[/math] после слияния

Алгоритм разделения AVL-дерева на два [ править ]

Алгоритм первый [ править ]

Далее действуем по алгоритму и в итоге получаем (рис. 4):

Алгоритм второй [ править ]

АВЛ-дерево с O(1) бит в каждом узле [ править ]

Идея [ править ]

Операции [ править ]

Балансировка [ править ]

Тип вращения	Иллюстрация	Когда используется	Расстановка балансов
Малое левое вращение

1 вариант: [math]balance[a] = 0[/math] и [math]balance[b] = 0[/math]

Примеры [ править ]

Ниже приведены примеры добавления и удаления вершины с подписанными изменениями факторов баланса каждой вершины.

Источник

Русские Блоги

Что такое сбалансированное бинарное дерево (AVL)

предисловие

Wiki: вкомпьютерная наукав,AVL деревоБыл впервые изобретенСамобалансирующееся бинарное дерево поиска, В дереве AVL максимальная разница высот между двумя поддеревьями, соответствующими любому узлу, равна 1, поэтому она также называетсяВысоко сбалансированное дерево, Найти, вставить и удалить в среднем и наихудшем случаесложность времениЭто все <\ displaystyle O (\ log )>

, Добавление и удаление элементов может потребоваться заимствовать один или несколько разВращение дереваДля достижения ребалансировки дерева. Дерево AVL названо в честь его изобретателяG. M. Adelson-Velsky с Evgenii LandisОни опубликовали эту структуру данных в статье 1962 года «Алгоритм организации информации».

1 Почему должно быть сбалансированное бинарное дерево?

Дерево двоичного поиска может в некоторой степени повысить эффективность поиска, но когда упорядочена исходная последовательность, например, последовательность A = <1, 2, 3, 4, 5, 6>, дерево двоичного поиска строится, как показано на рисунке 1.1. Двоичное дерево поиска, построенное в соответствии с этой последовательностью, является деревом с прямым углом, и в то же время двоичное дерево вырождается в один связанный список, и эффективность поиска снижается до O (n).

Поиск элемента 6 в этом бинарном дереве поиска требует 6 поисков.

Эффективность поиска бинарного дерева поиска зависит от высоты дерева, поэтому поддержание минимальной высоты дерева может обеспечить эффективность поиска дерева. Та же самая последовательность A, которая хранится способом, показанным на рисунке 1.2, должна сравниваться только 3 раза при поиске элемента 6, и эффективность поиска удваивается.

Можно видеть, что когда число узлов является постоянным, левый и правый концы дерева поддерживаются сбалансированными, и эффективность поиска по дереву является самой высокой.

Такое дерево, у которого разность высот между левым и правым поддеревьями не превышает 1, является сбалансированным бинарным деревом.

2. Определение

Сбалансированное двоичное дерево поиска: Называется сбалансированным двоичным деревом. Математики из бывшего Советского СоюзаAdelse-Vэльскиль иLВысоко сбалансированное бинарное дерево, предложенное andis в 1962 году, также называется AVL-деревом в соответствии с английским именем ученого. Он имеет следующие свойства:

Значение баланса, такого как баланс, означает, что компоненты с обеих сторон примерно одинаковы.

Например, рисунок 2.1 не является сбалансированным двоичным деревом, потому что левое поддерево узла 60 не является сбалансированным двоичным деревом.

Рисунок 2.2 также не является сбалансированным двоичным деревом, потому что, хотя левое и правое поддеревья любого узла являются сбалансированными двоичными деревьями, разница в высоте превысила 1.

Рисунок 2.3НеСбалансировать двоичное дерево.

3. Баланс фактор

4. Узловая структура

Определите структуру узла сбалансированного двоичного дерева:

5. Дисбаланс и регулировка при вставке дерева AVL

Вставив узел 99 в сбалансированное двоичное дерево здесь, структура дерева становится:

На рисунке 5.2 дерево с узлом 66 в качестве родительского узла называетсяМинимальный дисбаланс поддерева。

Минимальный дисбаланс поддерева: Поиск недавно вставленного узла с первым коэффициентом балансаАбсолютная величинаПоддерево, корень которого больше 1, называется наименьшим несбалансированным поддеревом. Другими словами, несбалансированное дерево может иметь несколько несбалансированных поддеревьев одновременно. В это время, пока мы настраиваем наименьшее несбалансированное поддерево, мы можем настроить несбалансированное дерево на сбалансированное дерево.

Корректировка дисбаланса сбалансированного двоичного дерева в основном достигается путем вращения наименьшего поддерева дисбаланса, Есть два метода обработки в зависимости от направления вращения,Левая рука против Правая рука 。

Целью поворота является уменьшение высоты и баланса путем уменьшения высоты всего дерева. Там, где дерево на другой стороне высоко, поверните дерево на той стороне вверх.

5.1 Левая рука

(1) Правый потомок узла заменяет эту позицию узла (2) Левый потомок правого потомка становится правым поддеревом узла (3) Сам узел становится левым потомком правого потомка

Весь рабочий процесс показан на рисунке 5.1.2.

5.2 Правильно

Правая операция аналогична левой операции, и последовательность операций:

(1) Левый дочерний узел представляет этот узел. (2) Правое поддерево левого дочернего узла становится левым поддеревом узла. (3) Используйте этот узел в качестве правого поддерева левого дочернего узла.

6. Четыре способа вставить узлы в дерево AVL

Предполагая, что узлом дерева AVL является A, есть четыре операции, которые сделают разницу в высоте между левым и правым поддеревьями A больше 1, тем самым нарушая баланс исходного дерева AVL. Существует четыре типа узлов вставки сбалансированного двоичного дерева:

Конкретный анализ заключается в следующем:

6.1 Левый потомок левого потомка А вставляет узел (LL)

Вам нужно выполнить правый поворот только один раз.

Код реализации выглядит следующим образом:

6.2 Правый потомок правого потомка А вставляет узел (RR)

Вам нужно выполнить левый поворот только один раз.

Код реализации выглядит следующим образом:

6.3 Правый потомок левого потомка А вставляет узел (LR)

Если правое дочернее дерево E левого дочернего узла A вставлено в узел F, узел A становится несбалансированным, как показано на рисунке:

Коэффициент баланса A равен 2, если он все еще регулируется в соответствии с правым поворотом, измененный график будет выглядеть следующим образом:

После регулировки правой рукой было обнаружено, что дерево все еще не сбалансировано после регулировки, что указывает на то, что в этом случае простое выполнение операции правой рукой не может сбалансировать дерево. Затем этот метод вставки должен выполнить двухэтапную операцию, так что после поворотаПравый дочерний элемент левого дочернего узла исходного корневого узла используется в качестве нового корневого узла.。

(1) Выполните левостороннюю операцию на левом дочернем элементе B неуравновешенного узла A, что является операцией в вышеописанном случае RR. (2) Правая операция выполняется на несбалансированном узле A, то есть операция в вышеупомянутом случае LL.

Процесс настройки выглядит следующим образом:

Другими словами, после этих двух шагов,Правый дочерний узел E левого дочернего узла исходного корневого узла становится новым корневым узлом。

6.4 Вставить узел (RL) левого поддерева правого потомка A

Процесс вставки правого дочернего элемента в левый узел аналогичен процессу вставки левого дочернего элемента в правый узел, а также необходимо выполнить двухэтапную операцию, чтобы после поворотаЛевый дочерний элемент правого дочернего узла исходного корневого узла используется в качестве нового корневого узла.。

(1) Выполните правую операцию на правом дочернем элементе C неуравновешенного узла A, которая является операцией в описанной выше ситуации LL. (2) Выполните операцию левой руки на несбалансированном узле A, которая является операцией в случае RR выше.

Другими словами, после этих двух шагов,Левый дочерний узел D правого дочернего узла исходного корневого узла становится новым корневым узлом。

Вспомогательные коды, реализованные в вышеупомянутых четырех режимах вставки, следующие:

6.5 Резюме

7. Четыре способа удаления узлов в дереве AVL

Операции удаления дерева AVL и дерева двоичного поиска одинаковы и делятся на четыре случая:

(1) Удалить листовой узел (2) Удаленный узел имеет только левое поддерево (3) Удаленный узел имеет только правое поддерево (4) Удаленный узел имеет как левое, так и правое поддерево

Основные шаги операции удаления следующие:

Для исправления несбалансированного состояния, вызванного операцией удаления, можно понять, что операция удаления левого или правого поддерева эквивалентна операции вставки правого или левого поддерева, и затем соответствующий поворот выбирается в соответствии с четырьмя вставками. Все в порядке.

подводить итоги

Проблема ротации AVL может показаться сложной, но на самом деле, если вы лично используете ручку и бумагу для ее работы, она все еще хорошо понята.

Источник

АВЛ-дерево

АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

АВЛ — аббревиатура, образованная первыми буквами создателей (советских учёных) Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича.

Содержание

Общие свойства

В АВЛ-дереве высоты имеется не меньше узлов, где — число Фибоначчи. Поскольку ,

где — золотое сечение,

то имеем оценку на высоту АВЛ-дерева , где — число узлов. Следует помнить, что — мажоранта, и её можно использовать только для оценки (Например, если в дереве только два узла, значит в дереве два уровня, хотя ). Для точной оценки глубины дерева следует использовать пользовательскую подпрограмму.

Тип дерева можно описать так

AVL-условия можно проверить так

Балансировка

Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится высота R.

Данное вращение используется тогда, когда (высота b-поддерева — высота R) = 2 и высота С высота L.

В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться.

Также можно заметить, что большое вращение это комбинация правого и левого малого вращения.

Из-за условия балансированности высота дерева О(log(N)), где N- количество вершин, поэтому добавление элемента требует O(log(N)) операций.

Алгоритм добавления вершины

Показатель сбалансированности в дальнейшем будем интерпретировать как разность между высотой левого и правого поддерева, а алгоритм будет основаться на типе TAVLTree, описанном выше. Непосредственно при вставке (листу) присваивается нулевой баланс. Процесс включения вершины состоит из трех частей:

В третьей ситуации требуется определить балансировку левого поддерева. Если левое поддерево этой вершины (Tree^.left^.left) выше правого (Tree^.left^.right), то требуется большое правое вращение, иначе хватит малого правого. Аналогичные (симметричные) рассуждения можно привести и для включение в правое поддерево.

вспомогательная функция сравнивающая два ключа

Рекурсивная процедура вставки:

Алгоритм удаления вершины

Упрощённый вариант удаления можно описать таким образом

Докажем, что данный алгоритм сохраняет балансировку. Для этого докажем по индукции по высоте дерева, что после удаления некоторой вершины из дерева и последующей балансировки высота дерева уменьшается не более, чем на 1. База индукции: Для листа очевидно верно. Шаг индукции: Либо условие балансированности в корне (после удаления корень может изменится) не нарушилось, тогда высота данного дерева не изменилась, либо уменьшилось строго меньшее из поддеревьев => высота до балансировки не изменилась => после уменьшится не более чем на 1.

Очевидно, в результате указанных действий процедура удаления вызывается не более 3 раз, так как у вершины, удаляемой по 2-му вызову, нет одного из поддеревьев. Но поиск ближайшего каждый раз требует O(N) операций, отсюда видна очевидная оптимизация: поиск ближайшей вершины производится по краю поддерева. Отсюда количество действий O(log(N)).

Нерекурсивная вставка в АВЛ-дерево сверху-вниз

Нерекурсивный алгоритм сложнее чем рекурсивная реализация.

Нерекурсивное удаление из АВЛ-дерева сверху-вниз

Для реализации удаления будем исходить из того же принципа что и при вставке, будем искать вершину, удаление из которой не приведёт к изменению её высоты, существуют всего два таких варианта

Сам алгоритм без всех оптимизаций для упрощения его понимания. В отличие от рекурсивного алгоритма при нахождении удаляемой вершины она будет заменена значением из левой подветви, данный алгоритм можно оптимизировать так же как и для рекурсивной версии за счёт того что после нахождения удаляемой вершины направление движения нам известно

Расстановка балансов при удалении

Как уже говорилось, если удаляемая вершина — лист, то она удаляется, и обратный обход дерева происходит от родителя удалённого листа. Если не лист — ей находится «замена», и обратный обход дерева происходит от родителя «замены». Непосредственно после удаления элемента — «замена» получает баланс удаляемого узла.

При обратном обходе: если при переходе к родителю пришли слева — баланс увеличивается на 1, если же пришли справа — уменьшается на 1.

Это делается до тех пор, пока при изменении баланса он не станет равным −1 или 1 (обратите внимание на различие с вставкой элемента!): в данном случае такое изменение баланса будет гласить о неизменной дельта-высоте поддеревьев. Повороты происходят по тем же правилам, что и при вставке.

Расстановка балансов при одинарном повороте

Если поворот осуществляется при вставке элемента, то баланс Pivot’а равен либо 1, либо −1. В таком случае после поворота балансы обоих устанавливаются равными 0.

При удалении всё иначе: баланс Pivot’а может стать равным 0 (в этом легко убедиться).

Приведём сводную таблицу зависимости финальных балансов от направления поворота и исходного баланса узла Pivot:

Тип вращения	Иллюстрация	Факторы балансов до вращения	Факторы балансов после вращения
Малое левое вращение

Расстановка балансов при двойном повороте

Pivot и Current — те же самые, но добавляется третий участник поворота. Обозначим его за «Bottom»: это (при двойном правом повороте) левый сын Pivot’а, а при двойном левом — правый сын Pivot’а.

При данном повороте — Bottom в результате всегда приобретает баланс 0, но от его исходного баланса зависит расстановка балансов для Pivot и Current.

Приведём сводную таблицу зависимости финальных балансов от направления поворота и исходного баланса узла Bottom:

Оценка эффективности

Г.М.Адельсон-Вельский и Е.М.Ландис доказали теорему, согласно которой высота АВЛ-дерева с N внутренними вершинами заключена между log2(N+1) и 1.4404*log2(N+2)-0.328, то есть высота АВЛ-дерева никогда не превысит высоту идеально сбалансированного дерева более, чем на 45%. Для больших N имеет место оценка 1.04*log2(N). Таким образом, выполнение основных операций 1 – 3 требует порядка log₂(N) сравнений. Экспериментально выяснено, что одна балансировка приходится на каждые два включения и на каждые пять исключений.

Источник