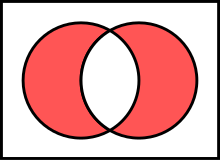
Доказать что 2 m группа относительно операции симметрической разности

Симметрическая разность

Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них. Симметрическая разность множеств и обозначается как В некоторых источниках используется другое обозначение:

Содержание

Определение

Симметрическую разность можно ввести двумя способами:

Понятие симметрической разности можно обобщить на число множеств, большее двух.

Свойства

Пример

См. также

Литература

Полезное

Смотреть что такое «Симметрическая разность» в других словарях:

СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — множеств одна из операций над множествами. Пусть имеются два множества Аи В. Тогда их симметрическая разность обозначается ADB и определяется равенствами где символы означают соответственно операции объединения, пересечения, разности и дополнения … Математическая энциклопедия

СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — порядка пв точке хфункции действительного переменного f(x) выражение Часто также симметрич. разностью называют выражение получающееся из вышеприведенного заменой hна 2h. Если функция f(x).имеет в точке хпроизводную fn (х).порядка п, то Т. П.… … Математическая энциклопедия

Разность множеств — Не следует путать с Симметрическая разность. Разность двух множеств это теоретико множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно… … Википедия

АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия

Симметричность — может означать: Симметрия Симметричная операция (от нескольких операндов) Симметричная функция (от нескольких переменных) Симметрический многочлен в математической логике: Симметричное отношение в линейной алгебре: Симметричный тензор… … Википедия

Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия

Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия

Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия

ИСЧИСЛЕНИЕ КЛАССОВ — аксиоматич. (см. Аксиоматический метод) описание логики классов. И. к. рав нообъёмно исчислению одноместных предикатов (см. Логика предикатов): у этих исчислений совпадают классы как исходных формул, так и выводимых формул (теорем);… … Философская энциклопедия

Источник

> знак равно <\ Displaystyle

>

СОДЕРЖАНИЕ

Характеристики

А \ треугольник В \ треугольник С> △ <\ Displaystyle

> знак равно <\ Displaystyle

>

Симметричная разница также может быть выражена с помощью операции XOR ⊕ для предикатов, описывающих два набора в нотации создателя множеств :

Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :

Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. Особенно:

Пересечение распределяется по симметричной разнице:

К другим свойствам симметричной разницы относятся:

Эта операция имеет те же свойства, что и симметричная разность множеств.

Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством множеств, дающей набор элементов, которые находятся в нечетном количестве множеств.

Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:

Симметричная разность на пространствах с мерой

Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.

является псевдометрикой на Σ. d _μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X

Расстояние Хаусдорфа против симметричной разности

Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.

Источник

П р и м е р 7. Множество многочленов K[x1. xn ], где K коммутативное ассоциативное кольцо с единицей, также коммутативное ассоциативное кольцо с единицей.

Определение 11.3. Элемент a1 кольца с единицей называется обратным к элементу a, если aa1 = a1 a = 1 (в коммутативном кольце достаточно требовать, чтобы aa1 = 1).

Так же, как в случае группы, доказывается, что элемент ассоциативного кольца с единицей не может иметь двух различных обратных элементов (но может не иметь ни одного). Элемент, имеющий обратный, называется обратимым.

Определение 11.4. Полем называется коммутативное ассоциативное кольцо с единицей, содержащее не менее двух элементов, в котором всякий ненулевой элемент обратим.

Примерами полей служат поле рациональных чисел Q, поле вещественных чисел R, поле комплексных чисел C. Мы знаем, что если p простое число, то кольцо классов вычетов Zp есть поле. Кольцо Z не является полем: в нем обратимы только ±1.

Если a, b произвольные элементы поля K и b = 0, то в K определен элемент ab1. Для этого элемента часто используют запись Любое поле обладает следующим важным свойством:

В самом деле, если a = 0, то, умножая обе части равенства ab = на a1, получаем b = 0. Существуют и другие кольца, обладающие этим свойством, например, кольцо Z. Они называются кольцами без делителей нуля. В кольце без делителей нуля возможно сокращение:

В самом деле, равенство ac = bc может быть переписано в виде (a b)c = 0, откуда при c = 0 получаем a b = 0, т. е. a = b.

Определение 11.5. Ненулевые элементы a, b кольца K называются делителями нуля, если ab = 0.

Приведем пример коммутативного ассоциативного кольца с делителями нуля.

П р и м е р 8. В кольце функций на подмножестве X числовой прямой (см. пример 3) есть делители нуля, если только X содержит более одной точки. В самом деле, разобьем X на два непустых непересекающихся подмножества X1, X2 и положим при i = 1, Тогда f1 f2 = 0, но f1 = 0, f2 = 0.

Кольца Zn, где n не простое, и Mn (K) также имеют делители нуля.

Отсутствие делителей нуля в поле означает, что произведение любых двух ненулевых элементов также является ненулевым элементом.

Пусть K ассоциативное кольцо с единицей. Обозначим через K множество обратимых элементов кольца K.

Предложение 11.1. Множество K является группой. Она называется мультипликативной группой кольца K.

Доказательство. Достаточно проверить, что операция умножения определена на K. Пусть a, b K. Тогда (ab)1 = b1 a1, откуда В поле K все ненулевые элементы обратимы. Они образуют абелеву группу относительно умножения, которая называется мультипликативной группой поля K и обозначается через K.

одной переменной, то P [x] = P.

Определение 11.6. Подмножество L кольца K называется подкольцом, если 1) L подгруппа аддитивной группы кольца K;

2) L замкнуто относительно умножения, т. е. для любых a, b L элемент ab L.

Очевидно, что всякое подкольцо L кольца K само является кольцом относительно операций кольца K. При этом оно наследует такие свойства, как коммутативность и ассоциативность.

П р и м е р 11. При любом n Z множество nZ является подкольцом кольца Z.

П р и м е р 12. Множество a + b d | a, b Z, где d фиксированное целое число, является подкольцом в C.

Определение 11.7. Подмножество L = <0>поля K называется подполем, если 1) L является подкольцом кольца K;

Говорят также, что K расширение поля L.

Очевидно, что всякое подполе L поля K является полем относительно операций поля K.

П р и м е р 13. Поле Q подполе поля R, поле R подполе поля C.

П р и м е р 14. Множество , где d фиксированное целое число, является подполем в C.

подмножеств. Доказать, что 2X кольцо относительно операций симметрической разности M N = (M \ N ) (N \ M ) и пересечения, взятых в качестве сложения и умножения соответственно. Доказать, что это кольцо коммутативно и ассоциативно.

2. Какие из следующих числовых множеств образуют кольцо, а какие поле относительно обычных операций сложения и умножения:

а) множество nZ, n 1;

б) множество рациональных чисел, в несократимой записи которых знаменатели делят фиксированное число n N;

в) множество рациональных чисел, в несократимой записи которых знаменатели не делятся на фиксированное простое число p;

г) множество рациональных чисел, в несократимой записи которых знаменатели являются степенями фиксированного простого числа p;

д) множество вещественных чисел вида x + y 2, где x, y Q;

е) множество вещественных чисел вида x + y 3 2, где x, y Q;

ж) множество вещественных чисел вида x + y 3 2 + z 3 4, где x, y Q;

з) множество комплексных чисел вида x + yi, где а) x, y Z;

и) множество всевозможных сумм вида a1 z1 + · · · an zn, где ai Q, zi комплексный корень степени n из 1, 1 i n.

3. Какие из указанных множеств матриц образуют кольцо относительно матричного сложения и умножения:

а) множество вещественных симметрических (кососимметрических) матриц порядка n;

б) множество вещественных ортогональных матриц порядка n;

в) множество верхних (нижних) треугольных матриц порядка г) множество матриц порядка n 2, у которых последние две строки нулевые;

д) множество матриц вида, где D фиксированное цеDy x лое число, x, y Z;

4. Какие из множеств функций образуют кольцо относительно обычных операций сложения и умножения функций:

2) множество функций, имеющих вторую производную на интервале (a, b);

3) множество функций вещественного переменного, обращающихся в 0 на некотором подмножестве D R;

4) множество тригонометрических многочленов с вещественными коэффициентами, где n произвольное натуральное число.

5. Во множестве многочленов от переменной t с обычным сложением рассматривается операция умножения, заданная правилом Является ли это множество кольцом?

6. Найти все обратимые элементы и все делители нуля в кольцах:

1) верхних треугольных матриц над полем; 2) M2 (R); 3) Z; 4) Z[i].

7. Пусть K = a + b 3 | a, b Z. Доказать, что группа обратимых элементов K бесконечна.

8. Докажите, что матрицы с элементами из Z2 образуют поле относительно обычных операций сложения и умножения матриц.

9. Доказать, что все конечные подмножества множества X образуют подкольцо кольца 2X из упражнения 1 к § 11.

10. Найдите все подкольца колец Z10, Z20 и Z7.

11. Докажите, что пересечение подколец кольца K является подкольцом кольца K.

12. Докажите, что пересечение подполей поля P подполе поля P.

13. Может ли в кольце, не являющемся полем, содержаться некоторое подполе?

14. Найдите в R наименьшее подкольцо с единицей и наименьшее подполе, содержащие число: 1) 2; 2) 3 2.

§ 12. ГОМОМОРФИЗМ, ИЗОМОРФИЗМ,

ЯДРО ГОМОМОРФИЗМА

Определение 12.1. Отображение f кольца A в кольцо B называется гомоморфизмом, если оно сохраняет операции, т. е. если для любых x, y A. Если гомоморфизм f является биекцией, то он называется изоморфизмом.

Изоморфизм кольца на себя называется автоморфизмом.

Отметим следующие свойства гомоморфизмов и изоморфизмов:

1. Тождественное отображение id : A A является изоморфизмом.

Доказательство. В самом деле, K подгруппа аддитивной группы кольца A, значит, f (K) подгруппа аддитивной группы кольца B.

Если y1, y2 f (K), то существуют x1, x2 K, такие, что f (x1 ) = y1, f (x2 ) = y2. Тогда Значит, f (K) подкольцо в B.

Во втором случае K1 подгруппа аддитивной группы кольца B, значит, по предложению 5.3 f 1 (K1 ) подгруппа аддитивной группы кольца A. Если x1, x2 f 1 (K1 ), то f (x1 ), f (x2 ) K1 и Значит, f 1 (K1 ) подкольцо в A.

то f (1A ) единица кольца f (A).

Действительно, Отметим, что не всегда f (1A ) будет являться единицей кольца B.

обычными операциями сложения и умножения матриц, B = M2 (R) =. Ясно, что отображение f : A B, f (x) = x, является гомоморфизмом, но f (1A ) = 1A = 1B.

Приведем два примера изоморфизмов колец.

П р и м е р 1. Отображение f : C C, f (z) = z, является изоморфизмом.

верить, что K кольцо относительно обычных операций сложения и умножения матриц. Рассмотрим отображение Тогда f изоморфизм.

Определение 12.2. Если f : A B гомоморфизм, то множество называется ядром гомоморфизма f.

Предложение 12.2. Ker f является подкольцом в A.

Доказательство. Так как f : A B гомоморфизм аддитивных групп колец A и B, то Ker f подгруппа аддитивной группы кольца A.

Если a, b Ker f, то Значит, Ker f подкольцо в A.

1. Доказать, что образ коммутативного кольца при гомоморфизме является коммутативным кольцом.

2. Пусть K поле, c K. Доказать, что отображение : K[x] K, f (x) f (c), гомоморфизм. Найти ядро.

3. Пусть K поле, f K[x] фиксированный многочлен. Доказать, что отображение : K[x] K[x], g(x) g(f (x)), является гомоморфизмом.

4. Найти все гомоморфизмы колец:

Определение 13.1. Подкольцо I кольца K называется левым идеалом, если для любого a K множество aI = содержится в I.

Подкольцо I кольца K называется правым идеалом, если для любого a K множество Ia = содержится в I.

Подкольцо I кольца K называется двусторонним идеалом (или просто идеалом), если I одновременно является левым и правым идеалом.

Если K коммутативное кольцо, то понятия левого, правого и двустороннего идеалов совпадают.

Предложение 13.1. Если f : A B гомоморфизм колец, то Ker f идеал в A.

Доказательство. Для любых элементов a A, x I = Ker f имеем откуда ax, xa I. Значит, I двусторонний идеал.

П р и м е р 1. <0>и K идеалы в любом кольце K. Их называют тривиальными идеалами.

Предложение 13.2. Пусть K коммутативное ассоциативное кольцо с 1. Для любых элементов a1. an K множество является идеалом в K. Его называют идеалом, порожденным элементами a1. an и обозначают (a1. an ).

+an yn произвольные элементы из I, z K, то откуда получаем, что I идеал.

Определение 13.2. Идеал, порожденный одним элементом a K, называют главным идеалом, порожденным элементом a, и обозначают (a) (либо aK).

Теорема 13.1 (Критерий поля). Пусть K коммутативное ассоциативное кольцо с 1 и 1 = 0. Если K не содержит нетривиальных идеалов, то K является полем.

Доказательство. Достаточно доказать, что любой ненулевой элемент a K имеет обратный a1. Рассмотрим главный идеал (a). Так как (a) = <0>, то по условию теоремы (a) = K. Значит, 1 (a), т. е.

существует элемент b K, такой, что 1 = ab. Следовательно, a обратим.

Предложение 13.3. Пусть I идеал в K, где K ассоциативное кольцо с 1. Если I содержит обратимый элемент a, то I = K.

Доказательство. Из условия следует, что 1 = aa1 I. Тогда для любого z K имеем 1z = z I, откуда I = K.

Следствие 13.1. Поле K содержит только тривиальные идеалы.

Доказательство. Если I ненулевой идеал в K, то I содержит ненулевой элемент, который обратим по определению поля. По предложению 13.3 I = K.

Пусть K кольцо, I идеал в K. Так как I подгруппа аддитивной группы K, то определена факторгруппа K/I. Элементы этой факторгруппы имеют вид a+I, a K, и называются смежными классами K по I. Определим умножение смежных классов формулой Докажем, что таким образом определенное умножение не зависит от выбора представителей в смежных классах.

Предложение 13.4. Если a + I = a1 + I и b + I = b1 + I, то ab + I = a1 b1 + I.

Доказательство. Из равенства смежных классов a + I = a1 + I и b + I = b1 + I следует по предложению 4.2, что a1 a, b1 b I. Тогда откуда снова по предложению 4.2 ab + I = a1 b1 + I.

Замечание 1. Когда мы рассматривали умножение смежных классов в факторгруппе G/N, то имели не только формально определенное равенство gN · hN = ghN. Фактически множество, состоящее из попарных произведений элементов двух смежных классов gN и hN группы G, совпадало со смежным классом ghN. Иначе обстоит дело в кольцах. В общем случае множество M = не совпадает со смежным классом ab+I, а лишь содержится в нем. Например, поэлементное произведение двух смежных классов 2 + 4Z и 2 + 4Z дает множество M = <4 + 8t | t Z>, и ясно, что M 4 + 4Z = 4Z.

K/I с операциями (a + I) + (b + I) = a + b + I, (aI)(bI) = abI является кольцом, которое называют факторкольцом кольца K по идеалу I.

Доказательство. Достаточно проверить дистрибутивность умножения относительно сложения. Для любых a + I, b + I, c + I K/I имеем Теорема доказана.

является сюръективным гомоморфизмом колец, и Ker f = I. Этот гомоморфизм называется каноническим.

Доказательство. Для любых a, b K имеем Сюръективность f очевидна. Кроме того, откуда Ker f = I.

Теорема 13.3 (Основная теорема о гомоморфизмах колец). Пусть f : A B гомоморфизм колец, I = Ker f. Тогда Доказательство. Так как f гомоморфизм аддитивных групп A и B, то по основной теореме о гомоморфизмах групп f (A) и A/I изоморфны как абелевы группы. Соответствующий изоморфизм :

A/I f (A) задается формулой (a + I) = f (a). Остается доказать, что сохраняет умножение. Для любых a + I, b + I A/I имеем ((a + I)(b + I)) = (ab + I) = f (ab) = f (a)f (b) = (a + I)(b + I), что и завершает доказательство теоремы.

Доказательство. По предложению 12.1 f (I) и f 1 (J) подкольца в f (A) и A соответственно. Если x f (A), y f (I), то x = f (a), y = f (b) для некоторых элементов a A, b I. Тогда поскольку ab I. Значит, f (I) идеал в f (A).

Далее, если x f 1 (J), a A, то f (ax) = f (a)f (x) J, поскольку f (x) J, а J идеал. Значит, ax f 1 (J) и f 1 (J) идеал в A.

1. Доказать, что пересечение идеалов (левых, правых, двусторонних) кольца K является идеалом (соответственно левым, правым, двусторонним).

2. Будут ли следующие множества идеалами указанных ниже колец:

г) множество In многочленов, не содержащих членов вида axk для всех k n, где n 1, в кольце Z[x];

д) множество I многочленов с четными свободными членами в кольце Z[x];

е) множество I многочленов с четными старшими коэффициентами в кольце Z[x].

3. Образуют ли идеал необратимые элементы колец:

4. Доказать, что кольцо целых чисел не содержит минимальных идеалов.

5. Пусть I и J множества матриц вида с целыми коэффициентами g, h, k. Доказать, что I является идеалом в кольце R верхних треугольных матриц над Z, J идеал кольца I, но J не идеал кольца R.

6. Доказать, что множество IS непрерывных функций, обращающихся в 0 на фиксированном подмножестве S [a, b], является идеалом в кольце функций, непрерывных на [a, b].

7. Суммой идеалов I1, I2. Ik коммутативного кольца R называется множество Доказать, что сумма идеалов является идеалом.

8. Произведением идеалов I1, I2 коммутативного кольца R называется множество Доказать, что произведение идеалов является идеалом.

9. Доказать, что если I1, I2 идеалы коммутативного кольца R и I1 I2 = <0>, то I1 I2 = <0>.

10. Доказать, что f : K R, A tr A, гомоморфизм. Найдите его ядро и факторкольцо K/ ker f.

Предположим, что А коммутативное ассоциативное кольцо с единицей.

Определение 14.1. Кольцо A без делителей нуля называется кольцом главных идеалов, если любой идеал в A является главным.

Теорема 14.1. Z кольцо главных идеалов.

Доказательство. Пусть I Z идеал, m наименьшее натуральное число в I и a I. Разделим a на m с остатком:

Так как a, m I, то a mq = r I, откуда r = 0 и a = mq. Значит, Теорема 14.2. Пусть K поле. Тогда кольцо многочленов K[x] кольцо главных идеалов.

Доказательство. Пусть I K[x] идеал, f (x) = 0 многочлен наименьшей степени в I и g(x) I. Разделим g(x) на f (x) с остатком:

Так как f (x), g(x) I, то g(x) f (x)q(x) = r(x) I, откуда r(x) = и g(x) = f (x)q(x). Значит, I = = f (x).

Замечание 1. Доказательства этих двух теорем похожи. Фактически все следует из того, что и в Z, и в K[x] существует алгоритм деления с остатком. Кольца, в которых возможно производить деление элементов с остатком, называют евклидовыми. Евклидовы кольца кольца главных идеалов.

Не все кольца являются кольцами главных идеалов.

П р и м е р 1. Пусть K поле. Тогда кольцо многочленов от двух переменных K[x, y] не является кольцом главных идеалов. Рассмотрим множество Нетрудно проверить, что I нетривиальный идеал в K[x, y]. Допустим, что I главный идеал. Тогда I = (h(x, y)) для некоторого многочлена h(x, y) K[x, y]. Поскольку x, y I, мы должны иметь для некоторых многочленов f1 (x, y), f2 (x, y) K[x, y]. Сравнивая степени левых и правых частей в (14.1), получаем, что либо deg h(x, y) = 0, либо deg h(x, y) = 1.

В первом случае h(x, y) ненулевая константа, поэтому обратимый элемент кольца K[x, y]. Тогда по предложению 13.3 I = K[x, y] противоречие, поскольку элементы из K не принадлежат I.

Во втором случае мы получаем deg f1 (x, y) = deg f2 (x, y) = 0, т. е.

f1 (x, y) = a и f2 (x, y) = b ненулевые константы. Тогда из (14.1) получаем а это противоречие.

1. Пусть I множество всех многочленов с четными свободными членами в кольце Z[x]. Доказать, что:

а) I является идеалом, но не является главным идеалом в Z[x];

2. Найти идеал, порожденный множеством M, если:

3. В кольце Z найдите порождающий элемент идеалов:

а) (4) + (7); в) (6, 9) + (25, 35);

б) (6) (8); г) (9, 15, 18) (12, 21, 33).

4. Пусть F поле и f, g F [x]. Доказать, что (f ) (g) тогда и только тогда, когда g делит (f).

Определение 15.1. Собственный идеал I коммутативного ассоциативного кольца A с единицей называется максимальным, если I не содержится ни в одном большем собственном идеале J.

Теорема 15.1. Идеал I максимален тогда и только тогда, когда A/I поле.

Доказательство. Пусть I максимален. Докажем, что в факторкольце A/I нет нетривиальных идеалов. Пусть T нетривиальный идеал в A/I. Рассмотрим канонический гомоморфизм f : A A/I.

Тогда по предложению 13.6 J = f 1 (T ) идеал в A, содержащий I.

Следовательно, J = A и f (J) = T = A/I противоречие. Теперь по теореме 13.1 получаем, что A/I поле.

Предположим, что A/I поле, а идеал I немаксимальный.

Тогда существует идеал J I, J = A. По предложению 13.6 образ T = f (J) идеала J является идеалом в A/I, при этом T = <0>и T = A/I противоречие, поскольку A/I поле, а поле не содержит нетривиальных идеалов.

2. Идеал (f (x)) K[x], где K поле, максимален f (x) неприводимый многочлен.

Доказательство. Докажем пункт 2 теоремы, пункт 1 доказывается аналогично.

Пусть (f (x)) максимальный идеал в K[x]. Предположим, что f (x) = g(x)h(x), где deg g(x) 0 и deg h(x) 0. Тогда (g(x)) нетривиальный идеал, содержащий (f (x)) и не совпадающий с ним, противоречие.

Пусть теперь f (x) неприводимый многочлен. Предположим, что идеал (f (x)) не максимален. Тогда найдется нетривиальный идеал (g(x)) (f (x)). Так как f (x) (g(x)), то f (x) = g(x)h(x), где h(x) не константа (иначе бы идеалы (f (x)) и (g(x)) совпадали). Получили противоречие с неприводимостью f (x).

Следствие 15.1. 1. Z/nZ поле n простое число.

2. K[x]/ f (x) поле f (x) неприводимый многочлен.

1. Для каких a факторкольцо Z7 [x]/(x2 a) является полем?

2. Является ли факторкольцо K/I полем, если:

3. Доказать, что факторкольцо K[x]/(x4 + x3 + x + 1) не может быть полем, каким бы ни было коммутативное кольцо K с единицей.

Используя понятие прямой суммы абелевых групп, определим прямую сумму колец.

Определение 16.1. Говорят, что кольцо A разлагается в прямую сумму своих подколец A1. Ak, если 1) аддитивная группа кольца A является прямой суммой аддитивных групп колец A1. Ak ;

Если кольцо A разлагается в прямую сумму своих подколец A1. Ak, то A1. Ak идеалы. Действительно, произвольный элемент a A можно представить в виде суммы a = a1 + · · · + ak, где ai Ai, i = 1. k. Тогда для произвольного элемента b Ai имеем Следовательно, Ai идеал.

Пусть теперь A1. Ak какие-то кольца.

Определение 16.2. Прямой суммой колец A1. Ak называется их прямая сумма A1 · · · Ak как аддитивных групп с покомпонентной операцией умножения:

Очевидно, что определенная таким образом операция умножения в A1 · · · Ak дистрибутивна по отношению к сложению, так что A1 · · · Ak действительно является кольцом. Если все кольца A1. Ak коммутативны, ассоциативны или обладают единицей, то и их прямая сумма обладает соответствующим свойством.

Прямая сумма колец в смысле определения 16.1 называется внутренней, а в смысле определения 16.2 внешней. Между этими двумя понятиями такая же связь, как и в случае групп или векторных пространств.

Для каждого кольца Ai рассмотрим гомоморфизм (x находится на i-м месте). Ясно, что i инъективен и по основной теореме о гомоморфизмах колец кольцо Ai изоморфно подкольцу Ai = i (Ai ) A. Нетрудно проверить, что Ai идеал в A. Непосредственно из определения идеалов Ai следует, что если i = j, то Ai Aj = <0>. Следовательно, A есть внутренняя прямая сумма своих подколец A1. Ak. Справедливо и обратное утверждение.

Доказательство. Из определения внутренней прямой суммы колец следует, что аддитивная группа кольца A является внутренней прямой суммой аддитивных подгрупп A1. Ak. По теореме 9.2 A и A1 · · · Ak изоморфны как аддитивные группы, причем изоморфизм задается формулой f ((x1. xk )) = x1 +· · ·+xk. В силу формул (16.1) и (16.2) f сохраняет умножение, следовательно, является изоморфизмом колец A и A1 · · · Ak.

Теорема 16.2. Пусть A1. Ak ассоциативные кольца с 1.

Тогда для мультипликативных групп справедливо равенство Доказательство. Элемент (x1. xk ) (A1 · · · Ak ) тогда и только тогда, когда существует (y1. yk ) A1 · · · Ak, такой, что i = 1. n. В свою очередь, это эквивалентно тому, что (x1. xk ) 1. Пусть R = I1 + I2 разложение коммутативного кольца R с единицей e в прямую сумму ненулевых идеалов I1, I2. Доказать, что если e = e1 + e2, где e1 I1, e2 I2, то e1, e2 единицы колец I1, I соответственно, но не единицы кольца R.

2. Пусть K поле. Доказать, что если многочлены f, g K[x] взаимно просты, то K[x]/(f g) K[x]/(f ) K[x]/(g).

3. Доказать, что если R = I1 + I2, то R/I1 I2, R/I2 I1.

4. Разложите кольца R[x]/(x2 + x), C[x]/(x2 + 1) в прямую сумму собственных идеалов.

натуральные числа. Тогда Доказательство. Рассмотрим отображение Вычисления показывают, что гомоморфизм. Проверим, что инъективно. Учитывая, что m и k взаимно просты, получаем:

(a + nZ) = (0 + mZ, 0 + kZ) m|a, k|a n = mk|a a + nZ = nZ.

Поскольку |Z/nZ| = n и |Z/mZ Z/kZ| = mk = n, то должно быть сюръективным отображением, а значит, является изоморфизмом.

Следствие 17.1. Пусть n натуральное число, n = ps1 · · · psk его разложение на простые множители. Тогда Доказательство. Очевидная индукция по k.

Теорема 17.2. Элемент a Z/nZ обратим (a, n) = 1.

Доказательство. Пусть a (Z/nZ). Тогда ax = 1 для некоторого элемента x Z/nZ. Это означает, что ax+nZ = 1+nZ, т. е. ax = 1+nt.

Следовательно, ax + n(t) = 1, откуда (a, n) = 1.

Обратно, пусть (a, n) = 1. Тогда существуют x, t Z, такие, что ax + nt = 1, откуда ax = 1 и a (Z/nZ).

Напомним понятие функции Эйлера. Если n натуральное число, то через (n) обозначают количество натуральных чисел, не превосходящих n и взаимно простых с n. Полученная функция, определенная на множестве натуральных чисел, называется функцией Эйлера.

Следствие 17.2. |(Z/nZ) | = (n).

Теорема 17.3. 1) Функция Эйлера обладает свойством мультипликативности, т. е. (mk) = (m)(k) для взаимно простых натуральных чисел m и k.

2) если n = ps1 · · · psk каноническое разложение натурального n на простые множители, то Доказательство. 1) По теореме 17. а по теореме 16. Учитывая теорему 17.2, получаем что и доказывает пункт 1) теоремы.

2) Очевидная индукция по k показывает, что если n = ps1 · · · psk, то справедливо равенство Поэтому достаточно уметь вычислять (pt ), где p простое число. По определению функции Эйлера (pt ) это количество целых чисел в промежутке от 1 до p, взаимно простых с pt, т. е. не делящихся на p.

Количество целых чисел из этого промежутка, делящихся на p, равно pt1, поскольку это числа вида pa, где 1 a pt1. Следовательно, откуда мы получаем p1 · · · pk = n, получаем второе утверждение теоремы.

Следствие 17.3. 1) Если a и n 1 взаимно простые натуn) ральные числа, то a на n равен 1 (теорема Эйлера).

2) Для простого числа p и произвольного a число ap a делится на p (теорема Ферма).

Доказательство. 1) Так как (a, n) = 1, то a (Z/nZ). Поскольку |(Z/nZ) | = (n), то по следствию 4.5 из теоремы Лагранжа получаем a(n) = 1 в Z/nZ. Следовательно, a(n) 1 (mod n).

2) Если p делит a, то, очевидно, ap a делится на p. Если p не делит a, то a и p взаимно просты. Так как (p) = p 1, то по теореме Эйлера ap1 1 делится на p. Значит, ap a также делится на p.

1. Доказать, что любая подгруппа аддитивной группы кольца Zn является идеалом кольца Zn и что Zn кольцо главных идеалов.

2. Найти все идеалы колец Z8, Z15. Какие из них максимальны?

3. Разложите в прямую сумму собственных идеалов кольца:

4. Пользуясь теоремой Эйлера, найти остаток при делении:

а) 208208 на 23; б) 102008 на 22.

ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Кольца, которые рассматриваются в этом параграфе, предполагаются коммутативными, ассоциативными и с единицей. Пусть дано кольцо R и независимые переменные x1. xn. Одночленом относительно этих переменных называется выражение axk1 · · · xkn, где коэфn фициент a R, а k1. kn целые неотрицательные числа. Показатели k1. kn называются степенями одночлена относительно соответствующих переменных, a k1 +· · ·+kn называется полной степенью или просто степенью одночлена. Если какая-то из степеней ki равна нулю, то выражение x0 в одночлене не пишут. Например, вместо x2 x0 x пишут x1 x3.

Два одночлена axk1 · · · xkn и bxk1 · · · xkn называют подобными. Для подобных одночленов определено сложение ( приведение подобных членов ). Для произвольных одночленов axk1 · · · xkn и bxm1 · · · xmn определено умножение:

Многочленом (или полиномом) называется формальная сумма одночленов, причем порядок слагаемых безразличен. Таким образом, любой многочлен можно записать в виде причем в сумме присутствует лишь конечное число одночленов с ненулевым коэффициентом ai1. in.

Элементы ai1. in R называют коэффициентами многочлена Многочлен, в котором все коэффициенты равны нулю, называется нулевым.

Максимальная из степеней одночленов, составляющих многочлен, называется его полной степенью или степенью и обозначается deg f.

Условимся считать, что нулевой многочлен имеет степень.

Многочлен, все одночлены которого имеют одинаковую степень s, называется однородным многочленом или формой степени s.

Максимальная из степеней одночленов относительно переменной xi называется степенью многочлена относительно этой переменной и обозначается degxi f.

Два многочлена считаются равными, если их разность нулевой многочлен, т. е. они являются суммой одинаковых одночленов.

Для многочленов естественным образом определяются действия сложения и умножения. Сумма двух многочленов это сумма всех одночленов, составляющих слагаемые; произведение это сумма произведений всех одночленов первого сомножителя на все одночлены второго.

Множество всех многочленов от переменных x1. xn над кольцом R обозначают R[x1. xn ]. Непосредственным вычислением нетрудно доказать следующее предложение.

Предложение 18.1. Кольцо многочленов R[x1. xn ] является ассоциативным и коммутативным кольцом с единицей.

Элемент a кольца R можно отождествить с многочленом ax0 · · · x и при таком отождествлении R является подкольцом в R[x1. xn ].

Любой многочлен f (x1. xn ) R[x1. xn ] можно записать в виде где fi (x1. xn1 ) R[x1. xn1 ], i = 0. s. Другими словами, Теорема 18.1. Если R кольцо без делителей нуля, то и кольцо многочленов R[x1. xn ] является кольцом без делителей нуля.

Доказательство. Применяем метод математической индукции по числу переменных. База индукции имеется для многочленов от одной переменной теорема была доказана ранее. Предположим, что кольцо многочленов от n 1 переменной не имеет делителей нуля. Тогда и кольцо многочленов от n переменных не имеет делителей нуля, поскольку в силу (18.1) оно является кольцом многочленов от одной переменной над кольцом многочленов от n 1 переменной R[x1. xn1 ], которое не имеет делителей нуля по индуктивному предположению.

Следствие 18.1. Если R кольцо без делителей нуля, то степень произведения двух многочленов из R[x1. xn ] равна сумме степеней сомножителей.

Доказательство. Пусть f, g R[x1. xn ]. Без ограничения общности можно считать, что f и g ненулевые многочлены (в противном случае утверждение теоремы тривиально). Собирая в f вместе одночлены одинаковой степени, запишем f в виде где fi форма степени i и fr = 0. Тогда степень f равна r. Аналогично g запишем в виде где gs = 0. Тогда степень g равна s и Все одночлены наибольшей степени, входящие в f g, содержатся в fr gs и имеют полную степень r+s. По теореме 18.1 fr gs = 0. Значит, степень f g равна r + s.

Предположим, что S кольцо, содержащее R, при этом единицы в R и S совпадают. Пусть дан многочлен и даны элементы b1. bn S.

Определение 18.1. Значением многочлена f (x1. xn ) в точке (b1. bn ) (или при x1 = b1. xn = bn ) называется Легко видеть, что если этом единицы в кольцах R и S совпадают. Для любых элементов b1. bn S существует единственный гомоморфизм для которого Доказательство. Определим отображение В силу (18.2) и (18.3) является гомоморфизмом. Докажем единственность. Если 1 : R[x1. xn ] S другой гомоморфизм, удовлеai1. in xk1 · · · xkn, то Значит, 1 =.

Пусть R кольцо без делителей нуля, содержащее бесконечно много элементов. Мы знаем, что в кольце многочленов R[x] от одной переменной каждый многочлен f (x) определяется своими значениями в d = deg f + 1 различных точках b1. bd. Другими словами, если g(bi ) = f (bi ), i = 1. d, для некоторого многочлена g(x) и deg g deg f, то g = f. В частности, никакие два неравных многочлена от одной переменной не могут принимать одинаковые значения в бесконечном количестве различных точек.

Ситуация меняется, когда мы рассматриваем многочлены от нескольких переменных. Например, многочлены x1 и x1 x2 из кольца R[x1, x2 ] принимают значение 0 во всех точках (0, b), где b R, однако они не равны. Тем не менее справедлива следующая теорема.

Теорема 18.2 (О тождестве). Если многочлены f1 (x1. xn ) и f2 (x1. xn ) принимают одинаковые значения во всех точках (b1. bn ), где b1. bn R, то они равны.

Доказательство. Для доказательства достаточно доказать следующее утверждение: если все значения многочлена h(x1. xn ) R[x1. xn ] во всех указанных в теореме точках равны нулю, то h нулевой многочлен. Действительно, достаточно перейти от многочленов f1 и f2 к их разности h = f1 f2.

Предположим, что h ненулевой многочлен. Покажем, что найдутся значения b1. bn для переменных x1. xn, при которых h принимает значение, отличное от нуля.

Применим метод математической индукции по числу переменных n. При n = 1 утверждение следует из того, что ненулевой многочлен от одной переменной имеет корней не больше, чем его степень. Действительно, по условию R бесконечное кольцо, и если бы все элементы из R являлись корнями h, то ненулевой многочлен h имел бы бесконечно много корней противоречие.

Пусть теперь n 1 и h(x1. xn ) ненулевой многочлен. Запишем h(x1. xn ) как многочлен от xn с коэффициентами из кольца R[x1. xn1 ]:

Можно считать, что as (x1. xn1 ) ненулевой многочлен. В силу индуктивного предположения найдется набор значений b1. bn из R, такой, что as (b1. bn1 ) = 0. Тогда где ci = ai (b1. bn1 ) и cs = 0. Поскольку теорема справедлива при n = 1, то найдется такое bn R, что что и требовалось доказать.

Можно немного ослабить требования теоремы 18.2. Оказывается, достаточно сравнивать значения многочленов не во всех точках из Rn, а только в точках из некоторого подмножества из Rn.

Следствие 18.2 (О несущественности алгебраических неравенств). Пусть R бесконечное кольцо без делителей нуля и пусть f1 и f2 два многочлена из R[x1. xn ], принимающие одинаковые значения во всех точках (b1. bn ), где выполнены неравенства где h1. hk отличные от нуля многочлены из R[x1. xn ]. Тогда многочлены f1 и f2 равны.

Доказательство. Рассмотрим многочлен (f1 f2 )h1 · · · hk. Он равен нулю при всех наборах переменных, так как там, где h1 = 0. hk = 0, обращается в нуль первый множитель. В силу теоремы о тождестве 18.2 (f1 f2 )h1 · · · hk = 0. Но R[x1. xn ] не имеет делителей нуля и h1 = 0. hk = 0. Следовательно, f1 f2 = 0, т. е. f1 = f2, что и требовалось доказать.

Установленная теорема полезна в ситуации, когда равенство значений двух многочленов удается установить в предположении о необращении в нуль одного или нескольких многочленов. В силу доказанной теоремы после установления такого равенства поставленные ограничения снимаются.

Замечание 1. Теорема о тождестве 18.2 перестает быть верной, если отбросить требование бесконечности кольца R. Например, в кольце многочленов Zp [x1, x2 ] рассмотрим многочлены f (x1, x2 ) = = xp x1 и g(x1, x2 ) = xp x2. По теореме Ферма ap a = 0 для любого a Zp. Следовательно, f (a, b) = g(a, b) = 0 для любой точки (a, b), где a, b Zp, но при этом f = g.

Для многочленов от одного неизвестного существует два естественных способа расположения членов по возрастающим и убывающим степеням неизвестного. В случае многочленов от нескольких неизвестных такие способы уже отсутствуют: если дан многочлен то его можно записать и в виде и нет оснований одну из этих записей предпочесть другой. Существует, однако, способ определенного расположения одночленов в многочлене от нескольких неизвестных. Этот способ зависит от выбора нумерации неизвестных, его называют лексикографическим и он подсказан обычным приемом расположения слов в словарях. Пусть даны два неподобных одночлена:

Определение 18.2. Говорят, что одночлен (18.4) выше одночлена (18.5), если первая отличная от нуля среди разностей k1 m1, k2 m2. kn mn положительна. В этом случае записываем axk1 · · · xkn bxm1 · · · xmn. Получаемое таким образом упорядочение на множестве одночленов называют лексикографическим.

Отношение лексикографического упорядочения одночленов обладает следующими свойствами:

Первое из этих свойств и дает основание называть отношение упорядочением.

Доказательство. 1) Пусть первая переменная, которая не входит во все одночлены A, B, C с одним и тем же показателем, входит в них с показателями k, l, m соответственно. Тогда по условию k l m, причем хотя бы в одном из двух случаев имеет место строгое неравенство.

Следовательно, k m, а это и означает, что A C.

2) При умножении на C к показателям, с которыми каждая из переменных входит в A и B, добавляется одно и то же число, и знак неравенства (или равенства) между этими показателями не меняется, а только эти неравенства и имеют значение при лексикографическом сравнении одночленов.

3) Пользуясь предыдущим свойством, получаем Предложение доказано.

Очевидно, что из любых двух различных одночленов многочлена f (x1. xn ) один будет выше другого. Записывая раньше тот из двух одночленов, входящих в f, который выше, получим лексикографическую запись f. Например, многочлен записан лексикографически. Обратите внимание: одночлен 3×2 x3 x3 лексикографически ниже одночлена x1, хотя его степень больше.

Определение 18.3. Высшим одночленом ненулевого многочлена f (x1. xn ) называется такой одночлен, который выше других одночленов, входящих в f.

Высший одночлен произведения многочленов h1. hk R[x1. xn ] равен произведению их высших одночленов.

Доказательство. Достаточно доказать это утверждение для двух многочленов, затем использовать очевидную индукцию по числу многочленов k. Пусть h1, h2 ненулевые многочлены с высшими одночленами A, B и A1, B1 их произвольные одночлены. Если A = A1 или B = B1, то в силу предложения 18. Это означает, что после приведения подобных слагаемых в произведении f1 f2 произведение AB сохранится в качестве ненулевого одночлена (ведь ему не с чем сокращаться), который выше остальных.

Замечание 2. Кроме лексикографического существуют и другие мономиальные упорядочения одночленов из R[x1. xn ], обладающие всеми свойствами из предложения 18.3. Каждое из этих упорядочений имеет свою область применения.

§ 19. СИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ В этом параграфе будем предполагать, что R ассоциативное коммутативное кольцо без делителей нуля.

Определение 19.1. Многочлен f R[x1. xn ] называется симметрическим, если он не изменяется ни при каких перестановках переменных.

Так как любая перестановка может быть осуществлена путем последовательных перестановок двух элементов, то многочлен является симметрическим, если он не изменяется при перестановке любых двух переменных.

П р и м е р 1. Степенные суммы sk = xk +· · ·+xk, k N, являются симметрическими многочленами.

П р и м е р 2. Следующие симметрические многочлены называются элементарными симметрическими многочленами:

Эти многочлены встречались ранее в курсе алгебры в связи с теоремой Виета.

Очевидно, что сумма, разность и произведение симметрических многочленов являются симметрическими многочленами. Иными словами, симметрические многочлены образуют подкольцо в кольце всех многочленов от n переменных.

Следовательно, если F R[y1. ym ] произвольный многочлен от m переменных y1. ym и f1. fm R[x1. xn ] какие-то симметрические многочлены от x1. xn, то значение F (f1. fm ) многочлена F при y1 = f1. ym = fm симметрический многочлен от x1. xn. Естественно возникает вопрос, нельзя ли найти такие симметрические многочлены f1. fm, чтобы всякий симметрический многочлен можно было выразить через них указанным способом. Оказывается, что в качестве таких многочленов можно взять элементарные симметрические многочлены 1. n.

Теорема 19.1 (Основная о симметрических многочленах ). Пусть f R[x1. xn ] симметрический многочлен. Тогда найдется такой многочлен F R[y1. yn ], что При этом многочлен F определен однозначно. Другими словами, всякий симметрический многочлен единственным образом представляется в виде многочлена от элементарных симметрических многочленов.

Для доказательства теоремы необходимы две леммы.

Лемма 19.1. Пусть u = axk1 xk2 · · · xkn высший одночлен симn метрического многочлена f. Тогда Доказательство. Предположим, что ki ki+1 для некоторого i.

Наряду с одночленом u многочлен f должен содержать одночлен получающийся из u перестановкой xi и xi+1. Легко видеть, что u u.

Это противоречит тому, что u старший одночлен многочлена f.

Лемма 19.2. Для любого одночлена u = axk1 xk2 · · · xkn, пока- n затели которого удовлетворяют неравенствам (19.1), существуют такие неотрицательные целые числа l1. ln, что высший одночлен многочлена al1 l2 · · · ln совпадает с u. Числа l1. ln определены этим условием однозначно.

Доказательство. Видно, что высший одночлен многочлена k равен x1 x2 · · · xk. В силу предложения 18.4 высший одночлен многочлена al1 l2 · · · ln равен axl1 (x1 x2 )l2 · · · (x1 x2 · · · xn )ln = axl1 +l2 +···+ln xl2 +l3 +···+ln · · · xln.

Приравнивая его одночлену u, получаем систему линейных уравнений Эта система имеет единственное решение:

Из условия леммы следует, что определенные таким образом числа l1. ln неотрицательны.

Доказательство теоремы 19.1. Если f = 0, можно взять F = 0. В противном случае пусть u1 = axk1 xk2 · · · xkn высший одночлен многоn члена f. По лемме 19.1 выполняются неравенства k1 k2. kn.

В силу леммы 19.2 существуют такие неотрицательные целые числа l1. ln, что высший одночлен многочлена al1 l2 · · · ln совпадает с u1. Обозначим F1 = ay1 y2 · · · yn K[y1. yn ] и рассмотрим симметрический многочлен Если f1 = 0, то можно взять F = F1. В противном случае пусть u высший одночлен многочлена f1. Ясно, что u1 u2. Снова по лемме 19.2 существует такой одночлен F2 K[y1. yn ], что высший одночлен многочлена F2 (1, 2. n ) равен u2. Рассмотрим симметрический многочлен Если f2 = 0, то можно взять F = F1 + F2. В противном случае, продолжая процесс, получаем последовательность симметрических многочленов f, f1, f2. высшие одночлены которых удовлетворяют неравенствам По лемме 19.2 показатель при любой переменной в любом из одночленов um не превосходит показателя при x1 в этом одночлене, а он, в свою очередь, не превосходит k1. Поэтому для наборов показателей одночленов um имеется лишь конечное число возможностей, так что описанный выше процесс должен оборваться. Это означает, что fM = для некоторого M. Тогда в качестве F можно взять F1 + F2 · · · + FM.

Докажем теперь, что многочлен F однозначно определен. Предположим, что F и G такие многочлены из K[y1. yn ], что Рассмотрим их разность H = F G. Тогда Нужно доказать, что H нулевой многочлен. Предположим, что это не так, и пусть H1, H2. Hs все ненулевые одночлены многочлена H. Обозначим через wi (i = 1, 2. s) высший одночлен многочлена В силу леммы 19.2 среди одночленов w1, w2. ws нет пропорциональных. Выберем наивысший из них. Пусть это будет w1. По построению одночлен w1 выше остальных одночленов многочлена H1 (1, 2. n ) и всех одночленов многочленов Hi (1, 2. n ) (i = 2. s). Поэтому после приведения подобных одночленов в сумме одночлен w1 сохранится (ему не с чем сокращаться), так что эта сумма не будет равна нулю, что противоречит нашему предположению.

Следующее утверждение позволяет по-новому осмыслить полученный в предыдущей теореме результат.

Предложение 19.1. Подкольцо S симметрических многочленов кольца R[x1. xn ] изоморфно кольцу многочленов R[x1. xn ].

Доказательство. Рассмотрим кольцо многочленов R[y1. yn ], которое изоморфно R[x1. xn ], и отображение т. е. в качестве (f ) мы берем значение f при y1 = 1. yn = n.

В силу предложения 18.2 гомоморфизм. Очевидно, Im S. По основной теореме о симметрических многочленах 19.1 любой симметрический многочлен h S можно представить в виде h = f (1. n ) для некоторого многочлена f R[y1. yn ]. Это означает, что h = = (f ), т. е. Im = S. Кроме того, отображение инъективно в силу единственности такого представления. Значит, изоморфизм колец Следуя доказательству этой теоремы, можно найти выражение любого конкретного симметрического многочлена через 1, 2. n.

На практике для однородных симметрических многочленов удобнее применять другой способ, который поясним на следующем примере.

П р и м е р 1. Выразим через 1, 2, 3, 4 многочлен В обозначениях доказательства теоремы 19.1 имеем u1 = x3 x2 x3 x4. He производя вычислений, можно найти с точностью до коэффициентов множество возможных кандидатов на роль одночленов u2, u3, u4.

Во-первых, их показатели должны удовлетворять неравенствам леммы 19.1. Во-вторых, поскольку f однородный многочлен степени 6, сумма их показателей должна равняться 6. В-третьих, они должны быть младше u1. Выпишем в таблицу все наборы показателей одночленов, удовлетворяющих этим условиям, в порядке лексикографического убывания, начиная с набора показателей одночлена u1, а справа выпишем соответствующие произведения элементарных симметрических многочленов, найденные по формулам (19.2):

Мы можем утверждать, что Чтобы найти коэффициенты a и b, будем придавать в этом равенстве переменным x1, x2, x3, x4 выбранные значения. Представим вычисления в виде таблицы, в правом столбце которой запишем получаемые уравнения:

Таким образом, a = 1 и b = 4, так что В случае неоднородного симметрического многочлена этот способ можно применить к каждой его однородной компоненте и полученные выражения сложить.

1. Следующие многочлены выразить в виде многочленов от элементарных симметрических многочленов:

в) (x1 x2 + x3 )(x1 x3 + x2 )(x2 x3 + x1 );

г) (x1 + x2 )(x1 + x3 )(x1 + x4 )(x2 + x3 )(x2 + x4 )(x3 + x4 ).

2. Найти значение симметрического многочлена F от корней многочлена f (x):

а) F = x3 (x2 +x3 )+x3 (x1 +x3 )+x3 (x1 +x2 ), f (x) = x3 x2 4x+1;

3. Решить над полем комплексных чисел систему уравнений 4. Доказать, что значение от корней степени n из 1 всякого симметрического многочлена от n переменных с целыми коэффициентами является целым числом.

5. Вычислить сумму пятых степеней корней многочлена x6 4×5 + +3×3 4×2 + x + 1.

6. Найти многочлен третьей степени, корнями которого являются:

а) кубы корней многочлена x3 x 1;

б) четвертые степени корней многочлена 2×3 x2 + 2.

КОЛЬЦА БЕЗ ДЕЛИТЕЛЕЙ НУЛЯ

Пусть A коммутативное ассоциативное кольцо без делителей нуля с единицей. Таким же образом, как кольцо целых чисел расширяется до поля рациональных чисел, кольцо A можно расширить до поля.

На множестве пар (a, b) A2, b = 0, определим отношение эквивалентности по правилу Рефлексивность и симметричность этого отношения очевидны; докажем его транзитивность. Если (a, b) (a1, b1 ) и (a1, b1 ) (a2, b2 ), то Поскольку b1 = 0 и A кольцо без делителей нуля, то обе части равенства можно сократить на b1. Получим т. е. (a, b) (a2, b2 ).

Класс эквивалентности, содержащий пару (a, b), условимся запиa сывать как дробь (пока это просто символ, не подразумевающий фактического деления). Множество всех дробей обозначим через Q(A).

Определим сложение и умножение дробей по правилам Лемма 20.1. Введенные операции над дробями корректно определены, т. е. не зависят от выбора представителей в классах эквивалентности.

Доказательство. Пусть =, =. Тогда ab1 = a1 b, cd1 = = c1 d. Имеем Проверим, что справа стоят равные дроби:

(ad + bc)b1 d1 (a1 d1 + b1 c1 )bd = (ab1 a1 b)dd1 + (cd1 c1 d)bb1 = 0, что и требовалось. Аналогичное вычисление показывает корректность умножения.

Теорема 20.1. Q(A) относительно введенных операций является полем. Это поле называют полем частных кольца A Поэтому любое конечное множество дробей можно привести к общему знаменателю, а сложение дробей с одинаковыми знаменателями сводится к сложению их числителей. Поэтому сложение дробей коммутативно и ассоциативно. Дробь служит нулем для операции сложения дробей, а дробь противоположна дроби. Таким образом, дроби образуют абелеву группу относительно сложения.

Коммутативность и ассоциативность умножения очевидны. Следующая цепочка равенств доказывает дистрибутивность умножения дробей относительно сложения:

Единицей для операции умножения дробей служит дробь, а при a = 0 дробь обратна дроби.

Сложение и умножение дробей вида сводятся к соответствуюa b щим операциям над их числителями. Кроме того, = только при a = b. Следовательно, дроби такого вида образуют подкольцо, изоa морфное A. Условившись отождествлять дробь вида с элементом a кольца A, можем считать, что кольцо A содержится в поле Q(A).

Далее, поскольку то дробь равна отношению элементов a и b кольца A в поле Q(A). Таb ким образом, обозначение можно теперь понимать содержательным образом как деление элементов a и b в поле Q(A).

Следствие 20.1. Пусть A коммутативное ассоциативное кольцо с 1. Кольцо A содержится в некотором поле K тогда и только тогда, когда A кольцо без делителей нуля.

Доказательство. Если A кольцо без делителей нуля, то по теореме 20.1 существует поле частных Q(A) и A Q(A). Наоборот, если A содержится в некотором поле K, то поскольку в K нет делителей нуля, кольцо A является кольцом без делителей нуля.

П р и м е р 1. Поле частных кольца Z целых чисел есть поле Q рациональных чисел.

П р и м е р 2. Поле частных кольца K[x] многочленов над полем K называется полем рациональных функций над полем K и обозначается через K(x).

П р и м е р 3. Поле частных кольца K[x1. xn ] многочленов от n переменных над полем K называется полем рациональных функций от n переменных над полем K и обозначается через K(x1. xn ).

Определение 21.1. Если для любого натурального числа n элемент n · 1 = 1 + · · · + 1 поля P отличен от нуля, то говорят, что поле P имеет характеристику нуль; если же для некоторого натурального n элемент n · 1 равен нулю, то наименьшее такое натуральное n называется характеристикой поля P и P называется полем положительной характеристики. Характеристика поля P обозначается char P.

Примерами полей положительной характеристики служат все конечные поля; существуют и бесконечные поля, имеющие положительную характеристику. Например, поле рациональных функций K(x), где K конечное поле положительной характеристики, является бесконечным полем положительной характеристики. Поле Fp = Z/pZ, состоящее из p элементов, очевидно, имеет характеристику p. Поля Q, R, C имеют характеристику нуль.

Непосредственно из определения следует, что для любого расширения E F справедливо char E = char F.

Теорема 21.1. Если поле P имеет характеристику p, то число p простое.

Доказательство. Действительно, из равенства p = st, где s p, t p, вытекало бы равенство Так как в поле не может быть делителей нуля, то или s · 1 = 0 или t · 1 = 0, что противоречит определению характеристики поля.

Предложение 21.1. Если характеристика поля P равна p, то для любого элемента a P и любого n, делящегося на p, имеет место равенство n · a = 0. Если же char P = 0, 0 = a P и 0 = n Z, то na = 0.

Доказательство. Пусть char P = p и n = pn1. Тогда Если char P = 0, то из равенства na = (n · 1)a = 0 следовало бы n · 1 = 0. Так как характеристика поля равна нулю, то n = противоречие.

Предложение 21.2. Если поле P имеет характеристику p, то для любых элементов x, y P и любого натурального n Доказательство. Воспользуемся индукцией по n. При n = 1 нужно доказать, что По формуле бинома Ньютона Так как Cp = Значит, (x + y)p = xp + y p.

Предположим, что предложение верно при n = k 1 и докажем его при n = k.

По индукции предложение 21.2 нетрудно перенести на случай произвольного числа слагаемых:

1. Доказать, что любое конечное поле имеет положительную характеристику.

2. Существует ли бесконечное поле положительной характеристики?

3. Доказать, что в поле Zp выполняются равенства:

4. Пусть F поле и f F [x]. Доказать, что если характеристика поля F равна нулю, то f = 0 тогда и только тогда, когда f постоянный многочлен; если же характеристика поля F равна p 0, то f = тогда и только тогда, когда f (x) = g(xp ) для некоторого многочлена g F [x].

Если поле L содержит поле K, то говорят, что L является расширением поля K. В этом случае L можно рассматривать как векторное пространство над полем K. Действительно, по определению поля L является абелевой группой относительно сложения. Далее, поскольку K L, то определено умножение элементов поля K на элементы поля L, которые можно рассматривать как векторы. Фактически, это умножение является умножением элементов поля L. При этом из определения поля вытекают следующие свойства:

для любых элементов a, b K, x, y L. Это и означает, что L векторное пространство над полем K.

Определение 22.1. Размерность L над K называется степенью расширения L над K и обозначается [L : K]. Степень расширения может быть равна бесконечности.

Если [L : K], то говорят, что L конечное расширение поля K или что L конечно над K.

iI базис E над F и jJ базис F над K, то iI,jJ базис E над K.

Доказательство. Вначале докажем, что любой элемент x E можно выразить через xi yj, i I, j J, с коэффициентами из поля K. Так как iI базис E над F, то существуют элементы i F, среди которых лишь конечное число отлично от нуля, такие, что Так как jJ базис F над K, то для каждого ненулевого i существуют элементы ij K, среди которых лишь конечное число отлично от нуля, такие, что Подставляя (22.2) в (22.1), получаем что и требовалось.

Докажем, что элементы xi yj, i I, j J, линейно независимы над K. Предположим, что существуют элементы ij K, i I, j J, среди которых не все равны нулю и лишь конечное число отлично от нуля, такие, что Тогда Поскольку i = ij yj F, а элементы iI линейно независимы над F, то Следствие 22.1 (О мультипликативности степени расширений полей). Пусть E, F, K поля и E F K. Расширение E над K конечно тогда и только тогда, когда E конечно над F и F конечно над K. В случае их конечности справедливо соотношение Доказательство. Если E конечно над F и F конечно над K, то из теоремы 22.1 немедленно следует, что E конечно над K.

Если E конечно над K, то и F конечно над K, поскольку является подпространством в E. Далее, если e1. en базис E над K, то тем более элементы e1. en порождают E над F (хотя и не обязаны являться базисом E над F ). Значит, E конечно над F.

Формула (22.3) непосредственно следует из теоремы 22.1.

1. Доказать, что если L расширение поля K и степень [L : K] простое число, то единственными полями F, удовлетворяющими условию K F L, являются F = K и F = L.

Определение 23.1. Поле, не обладающее никаким собственным подполем, называется простым.

Доказательство. Если K Q подполе, то 1 K. Следовательно, 1 + · · · + 1 = n K для любого n Z, т. е. Z K. Для любых n, m Z, m = 0, дробь n/m K, поскольку K поле. Значит, K = Q.

любого n <0, 1. p 1>, т. е. Zp K. Значит, K = Zp.

Теорема 23.1. В любом поле P содержится ровно одно простое подполе P0. Если char P = 0, то P0 изоморфно Q. Если char P = p, то P0 изоморфно Zp.

Доказательство. Допустив существование двух различных простых подполей P0, P1 P, получим, что их пересечение будет полем, отличным от P0 и P1. Это, однако, невозможно ввиду их простоты.

Значит, простое подполе P0 P единственно.

Рассмотрим отображение f : Z P, определенное правилом f (n) = n·1. Отображение f гомоморфизм, а его ядро Ker f является идеалом в Z. Так как Z кольцо главных идеалов, то Ker f = mZ.

имеющие смысл в P (поскольку P поле), образуют поле P0, изоморфное Q. В силу предложения 23.1 P0 будет простым подполем в P.

Если char P = p, то m = p и мы имеем по основной теореме о гомоморфизмах для колец, что В силу предложения 23.1 P0 = f (Z) простое подполе в P, изоморфное Zp.

1. Доказать, что в поле из p2 элементов, где p простое число, имеется единственное собственное подполе.

2. Пусть K поле из n элементов. Какое простое подполе содержит K и чему равна характеристика K, если:

3. Какое простое подполе содержит следующее поле:

4. Доказать, что если Ki, i I, подполя в P, то K = iI Ki подполе в P.

§ 24. АЛГЕБРАИЧЕСКИЕ РАСШИРЕНИЯ ПОЛЕЙ

Определение 24.1. Пусть E F расширение полей. Элемент a E называется алгебраическим над F, если существует ненулевой многочлен f (x) F [x], такой, что f (a) = 0. Если такого многочлена не существует, т. е. для любого f (x) F [x] имеем f (a) = 0, то элемент a называется трансцендентным над F.

Определение 24.2. Пусть E F расширение полей и a E алгебраический элемент над F. Минимальным многочленом элемента a называется ненулевой многочлен f (x) F [x] наименьшей степени и со старшим коэффициентом 1, такой, что f (a) = 0. Степень многочлена f (x) называется степенью элемента a.

Лемма 24.1. Минимальный многочлен f (x) элемента a E неприводим.

Доказательство. Допустим, что f (x) = g(x)h(x), где deg g(x) deg f (x), deg h(x) deg f (x). Тогда откуда либо g(a) = 0 либо h(a) = 0 противоречие c минимальностью f (x).

Предложение 24.1. Если f (x) минимальный многочлен элемента a над полем F и g(a) = 0 для некоторого многочлена g(x) F [x], то g(x) делится на f (x).

Доказательство. Разделим g(x) на f (x) с остатком:

Подставив x = a, получим 0 = r(a), откуда r(x) = 0 (иначе мы имели бы противоречие с минимальностью f (x)).

Определение 24.3. Расширение полей E F называется алгебраическим, если все элементы из E являются алгебраическими над F.

Теорема 24.1. Любое конечное расширение E поля F является алгебраическим над F.

Доказательство. Пусть 0 = a E и [E : F ] = n. Тогда элементы 1, a, a2. an линейно зависимы над F. Значит, существуют элементы b0, b1. bn F, не все равные нулю и такие, что Пусть f (x) = b0 + b1 x + · · · + bn xn F [x]. Тогда f (x) = 0 и f (a) = 0.

Значит, a алгебраичен над F.

1. Найти минимальные многочлены для элементов:

над L элемент и f L[x]. Доказать, что элемент f (a) K является трансцендентным над L.

3. Доказать, что следующие числа являются алгебраическими над Q:

§ 25. ПРОСТЫЕ РАСШИРЕНИЯ ПОЛЕЙ Определение 25.1. Обозначим через F (a) наименьшее подполе в E, содержащее F и a. Переход от поля F к полю F (a) называется присоединением к F элемента a. Поля вида F (a) называются простыми расширениями поля F.

Абстрактно F (a) может быть описано как пересечение всех подполей поля E, содержащих F и a. Следующее предложение дает более конкретное описание F (a).

Следующие равенства показывают, что K подполе в E.

Очевидно, a K, F K. Значит, F (a) K.

С другой стороны, a F (a) по определению. Тогда f (a) F (a) для любого многочлена f (x) F [x]. Поскольку F (a) поле, то и все дроби, где f, g F [x], g(a) = 0, принадлежат F (a). Значит, K F (a). Таким образом, K = F (a).

Опишем вначале простые расширения поля F в случае, когда a является алгебраическим элементом над F (простые алгебраические расширения).

Теорема 25.1. Пусть E F расширение полей и a E алгебраический элемент степени n над F. Тогда Степень [F (a) : F ] равна степени минимального многочлена элемента a над F.

Доказательство. Пусть p(x) минимальный многочлен элемента a над F. Рассмотрим гомоморфизм Ядро является идеалом в F [x], а по теореме 14.2 F [x] кольцо главных идеалов. Поскольку по определению минимального многомногочлен наименьшей степени, содержащийся в ker, члена p(x) то ker = (p(x)). По основной теореме о гомоморфизмах колец, (F [x]) F [x]/(p(x)). Так как p(x) неприводим, то (p(x)) максимальный идеал по теореме 15.2. Следовательно, по теореме 15. F [x]/(p(x)) (F [x]) F (a) в силу предложения 25.1. Так как F (a) наименьшее подполе, содержащее F и a, то Если f (a) F (a), то разделив f (x) на p(x) с остатком, получим где r(x) F [x] и deg r(x) deg p(x) = n. Тогда т. е. любой элемент из F (a) имеет вид b0 + b1 a + b2 a2 + · · · + bn1 an1, где b0, b1. bn1 F, что и требовалось.

Итак, мы доказали, что элементы 1, a, a2. an1 порождают F (a) как векторное пространство над F. Докажем, что эти элементы линейно независимы над F. Пусть где b0, b1. bn1 F и не все из них равны нулю. Тогда s(a) = 0, где 0 = s(x) = b0 + b1 x +b2 x2 + · · · +bn1 xn1 F [x] и deg s(x) deg p(x) противоречие с минимальностью p(x).

Доказательство. Рассмотрим расширения полей F F (a) F (a)(b). Так как b алгебраичен над F, то b алгебраичен над F (a).

По теореме 25.1 F (a)(b) конечно над F (a) и F (a) конечно над F. Согласно следствию 22.1 F (a)(b) конечно над F. По теореме 24.1 F (a)(b) ский элемент над F.

Изучим случай простого трансцендентного расширения поля K.

поле рациональных функций от одной переменной над F.

Доказательство. Рассмотрим отображение Проверим корректность определения. Так как a трансцендентный элемент над F и g(x) = 0, то g(a) = 0 и можно вычислить элемент f (a)g1 (a) = f1 (a)g(a). В силу трансцендентности a имеем g(a) = 0, Легко проверить, что гомоморфизм и биекция.

1. Пусть L/K алгебраическое расширение. Доказать, что расширение L(x)/K(x) также алгебраическое и [L(x) : K(x)] = [L : K].

2. Пусть L/K и K/F алгебраические расширения. Доказать, что расширение L/F также алгебраическое.

3. Какой вид имеют элементы простых расширений:

б) Q(e2 ); г) Q(e 3 ); е) R(1 + 2i).

4. Докажите, что:

б) Q( p, q) = Q( p+ q), где p, q различные простые числа.

5. Докажите, что поля Q( p) и Q( q), где p, q различные простые числа, неизоморфны.

6. Найдите все автоморфизмы полей Q( 2), Q( 3 2).

7. Доказать, что расширение L/K является конечным тогда и только тогда, когда L может быть получено из K присоединением конечного числа алгебраических над K элементов.

§ 26. АЛГЕБРАИЧЕСКИ ЗАМКНУТЫЕ ПОЛЯ

Определение 26.1. Поле K называется алгебраически замкнутым, если любой отличный от константы многочлен из K[x] обладает в K хоть одним корнем.

Основная теорема алгебры утверждает, что поле C алгебраически замкнуто. Следующая теорема показывает, что существуют и другие алгебраически замкнутые поля.

Теорема 26.1 (Штейниц). Для каждого поля K существует алгебраически замкнутое алгебраическое расширение K. С точностью до изоморфизма, тождественного на поле K, поле K определено однозначно.

Доказательство теоремы Штейница выходит за рамки нашего курса, его можно найти в [9, гл. VII, § 2].

Поле K называется алгебраическим замыканием поля K.

полей, то алгебраическое замыкание E поля E является также алгебраическим замыканием поля F.

Доказательство. Достаточно доказать, что любой элемент a E алгебраичен над F. Элемент a алгебраичен над E. Пусть f (x) = = b0 + b1 x + · · · + bn xn E[x] минимальный многочлен a. Рассмотрим поле F1 = F (b0, b1. bn ), которое получается последовательным присоединением к F элементов b0, b1. bn. На каждом шаге мы имеем простое алебраическое расширение, которое является конечным расширением по теореме 25.1. В силу мультипликативности степени [F1 : F ]. Поскольку элемент a алгебраичен над F1 (коэффициенты минимального многочлена f (x) принадлежат F1 ), то F1 (a) конечное расширение F1. В силу мультипликативности степени F1 (a) конечное расширение F. Следовательно, F1 (a) алгебраическое расширение F и элемент a алгебраичен над F.

Ранее мы уже встретились с важным классом конечных полей, т. е.

полей, состоящих из конечного числа элементов. Было установлено, что для каждого простого числа p кольцо Zp является конечным полем, состоящим из p элементов.

Поле Zp играет важную роль в общей теории полей, так как, согласно теореме 23.1, каждое поле характеристики p должно содержать изоморфное Zp подполе и потому может рассматриваться как расширение поля Zp. Это замечание играет основную роль в классификации конечных полей, поскольку характеристика каждого конечного поля есть простое число.

Предложение 27.1. Пусть F конечное поле, содержащее подполе K из q элементов, m = [F : K]. Тогда |F | = q m.

Доказательство. Поле F можно рассматривать как векторное пространство над полем K. В силу конечности F это пространство конечномерно. Если [F : K] = m, то F имеет базис над полем K, состоящий из m элементов, скажем, b1. bm. Таким образом, каждый элемент поля F может быть однозначно представлен в виде линейной комбинации a1 b1 + am bm, где a1. am K. Так как каждый коэффициент ai может принимать q значений, то поле F состоит в точности из q m элементов.

Теорема 27.1. Пусть F конечное поле. Тогда оно состоит из pn элементов, где простое число p является характеристикой поля F, а натуральное число n является степенью поля F над его простым подполем Zp.

Доказательство. Так как поле F конечно, то его характеристика некоторое простое число p. Поэтому простое подполе K поля F изоморфно Zp и, значит, содержит p элементов. Остальное вытекает из предложения 27.1.

Чтобы установить, что для каждого простого p и каждого натурального n существует конечное поле из pn элементов, мы используем подход, подсказываемый следующей леммой.

Лемма 27.1. Если F конечное поле из q элементов, то каждый элемент a F является корнем многочлена xq x Fp [x].

Доказательство. Для a = 0 равенство aq = a выполняется тривиально. Что же касается ненулевых элементов поля F, то они образуют мультипликативную группу F порядка q 1, так что для каждого ненулевого элемента a F по следствию из теоремы Лагранжа выполняется равенство aq1 = 1, умножение которого на a приводит к требуемому результату.

Теперь докажем главную характеризационную теорему для конечных полей.

Теорема 27.2 (О существовании и единственности конечных полей). Для каждого простого числа p и каждого натурального числа n с точностью до изоморфизма существует единственное конечное поле из pn элементов.

Доказательство. Существование. Для q = pn рассмотрим многочлен xq x Fp [x], и пусть Fp алгебраическое замыкание поля Fp. Многочлен x x не имеет кратных корней в поле Fp, так как его производная является постоянным многочленом:

и в силу этого не может иметь общих корней с xq x. Поэтому многочлен xq x имеет q различных корней в поле Fp. Пусть Докажем, что F подполе поля Fp. Если a, b F, то, используя предложение 21.2, получаем откуда a + b, ab, a1 F. Далее, если p = 2, то 1 = 1 и (a)q = = aq = a = a. Если же p 2, то (a)q = aq = a. В обоих случаях получаем, что a F. Итак, F конечное поле из q элементов.

ментов. Тогда char F1 = char F2 = p и потому Fp простое подполе в F1 и F2. Пусть F 1 и F 2 алгебраические замыкания полей F1 и F2.

По предложению 26.1 F 1 и F 2 алгебраические замыкания поля Fp, а поэтому изоморфны. Пусть : F 1 F 2 изоморфизм.

Выше мы доказали, что поле F1 совпадает со множеством корней многочлена xq x в поле F 1, а поле F2 совпадает со множеством корней многочлена xq x в поле F 2. Если a F1, то aq a = 0. Применяя к обеим частям этого равенства изоморфизм, получим (a)q (a) = 0, откуда (a) F2. Значит, (F1 ) F2. Так как порядки F1 и F2 совпадают и инъективно, то (F1 ) = F2. Таким образом, ограничение на F1 является изоморфизмом полей F1 и F2.

Доказанная в теореме 27.2 единственность позволяет говорить о вполне определенном конечном поле данного порядка q. Будем обозначать его через Fq, где под q понимается степень некоторого простого числа p, которое и является характеристикой этого поля.

Теорема 27.3 (Критерий подполя конечного поля). Пусть q = pn, где p простое число. Тогда каждое подполе L поля Fq имеm ет порядок p, где m является делителем числа n. Обратно, если m делитель числа n, то существует ровно одно подполе L поля Fq, состоящее из pm элементов. При этом степень [Fq : L] =.

Доказательство. Ясно, что любое подполе L поля Fq должно иметь порядок pm, где m натуральное число, не превосходящее n.

Из предложения 27.1 следует, что число q = pn должно быть степенью числа pm, так что m обязательно делит число n.

Пусть Fp алгебраическое замыкание поля Fp. Тогда поле Fq совпадает со множеством корней многочлена xq x в поле Fp. Если m делитель числа n, т. е. n = md, то откуда pm 1 делит число pn 1. Следовательно, многочлен xp делит многочлен xp 1 1 = xq1 1 в Fp [x]. Значит, xp x делит многочлен xq x в Fp [x]. Таким образом, каждый корень многочлена xp x является корнем многочлена xq x и, значит, принадлежит полю Fq. Поэтому Fq должно содержать все корни многочлена xp x, а множество этих корней образует поле Fpm порядка pm.

Если бы поле Fq содержало два различных подполя порядка pm, то эти подполя содержали бы в совокупности больше чем pm корней многочлена xp x в поле Fq, а это невозможно.

И так как Fq L, то по предложению 27.1 q = pn = (pm )d, где d = [Fq : L]. Следовательно, d =.

П р и м е р 1. Подполя конечного поля F230 можно найти, составив список всех положительных делителей числа 30. Отношения включения между этими подполями указаны в следующей диаграмме.

Согласно теореме 27.3, эти отношения включения равносильны отношениям делимости соответствующих делителей числа 30.

Теорема 27.4. Любое конечное поле Fpn имеет в точности одно расширение L Fpn степени [L : Fpn ] = m для каждого m 1.

Доказательство. Докажем, что расширение L существует. Пусть L = Fpnm. По теореме 27.3 поле L содержит единственное подполе Fpn и степень [Fpnm : Fpn ] = m. Если L1 другое расширение со свойством [L1 : Fpn ] = m, то число элементов в L1 по предложению 27.1 равно (pn )m = pnm. В силу единственности поля из pnm элементов, поля L и L1 изоморфны.

Замечание 1. Теорему 27.4 нельзя перенести на поля нулевой характеристики. Например, если p и q различные простые числа, то поля Q( p) и Q( q) не изоморфны (см. упражнение 5 из § 26) и имеют степень два над Q. Таким образом, Q имеет бесконечно много неизоморфных расширений степени 2.

Следующий результат устанавливает одно важное свойство мультипликативной группы конечного поля.

Теорема 27.5 (О конечной мультипликативной подгруппе в поле). Пусть K произвольное поле, G конечная подгруппа в K. Тогда G циклическая группа. В частности, группа F цикq лическая.

pi, i = 1. s. По пункту 1 теоремы 9.5 циклическая группа Zn изоморфна прямому произведению H1 · · · Hs = G. Значит, G Zn и G циклическая группа.

Определение 27.1. Образующий элемент циклической группы Fq называется примитивным элементом поля Fq.

Из теоремы 27.5 следует, что поле Fq содержит (q 1) примитивных элементов, где функция Эйлера. Наличием в любом конечном поле примитивных элементов можно воспользоваться, например, для доказательства того факта, что каждое конечное поле является простым алгебраическим расширением своего простого подполя.

= Fq (a), где a любой примитивный элемент поля Fr.

Доказательство. Поле Fq (a) содержит 0 и все степени элемента a, а значит, все элементы поля Fr. Следовательно, Fq (a) = Fr.

Следствие 27.1. Для каждого конечного поля Fq и каждого натурального числа n в кольце Fq [x] существует неприводимый многочлен степени n.

Доказательство. Пусть Fr расширение поля Fq порядка q n, так что [Fr : Fq ] = n. Согласно теореме 27.6, существует такой элемент a Fr, что Fr = Fq (a). Тогда минимальный многочлен элемента a над Fq является неприводимым многочленом степени n в кольце Fq [x].

1. Доказать неприводимость над F2 многочлена f (x) = x3 +x+ F2 [x] и построить таблицы сложения и умножения для поля F2 (a), где a корень многочлена f. Сколько элементов содержит поле F2 (a)?

2. Доказать, что для каждого конечного поля, за исключением F2, сумма всех его элементов равна нулю.

3. Пусть a, b элементы поля F2n, где n нечетно. Доказать, что из равенства a2 + ab + b2 = 0 вытекает a = b = 0.

4. Доказать, что отображение f : Fpn Fpn, f (x) = xp, является автоморфизмом поля Fpn.

5. Пусть F поле. Доказать, что если его мультипликативная группа F циклическая, то F конечное поле.

6. Найти все примитивные элементы полей F7, F17.

7. Доказать, что любой элемент поля Fpn имеет в этом поле ровно один корень степени p.

8. Доказать, что для f Fq [x] верно равенство (f (x))q = f (xq ).

9. Доказать, что любой квадратный многочлен из Fq [x] разлагается над полем Fq2 на линейные множители.

10. Пусть Fq конечное поле характеристики p. Доказать, что многочлен f Fq [x] обладает свойством f (x) = 0 тогда и только тогда, когда f является p-й степенью некоторого многочлена из Fq [x].

11. Пусть F некоторое поле и отображение h : F F определяется условием h(a) = a1, если a = 0, и h(0) = 0. Доказать, что h является автоморфизмом поля F тогда и только тогда, когда F состоит не более чем из четырех элементов.

ЛИТЕРАТУРА

Атья, М. Введение в коммутативную алгебру / М. Атья, И. Макдональд. М., 1972.

Богопольский, О.В. Введение в теорию групп / О.В. Богопольский. М.-Ижевск, 2002.

Ван дер Варден, Б.Л. Алгебра / Б.Л. Ван дер Варден. М., 1979.

Винберг, Э.Б. Курс алгебры / Э.Б. Винберг. М., 2001.

Зарисский, О. Коммутативная алгебра / О. Зарисский, П. Самюэль. М., 1963.

Каргаполов, М.И. Основы теории групп / М.И. Каргаполов, Ю.И. Мерзляков.

Кострикин, А.И. Введение в алгебру. Ч.1. Основы алгебры / А.И. Кострикин.

Кострикин, А.И. Введение в алгебру. Ч.3. Основные структуры / А.И. Кострикин. М., 2001.

Курош, А.Г. Курс высшей алгебры / А.Г. Курош. М., 1968.

Ленг, С. Алгебра / С. Ленг. М., 1968.

Лидл, Р. Конечные поля / Р. Лидл, Г. Нидеррайтер. М., 1988.

Милованов, М.В. Алгебра и аналитическая геометрия / М.В. Милованов, Р.И. Тышкевич, А.С. Феденко. Минск, 2001. Т.1.

Фаддеев, Д.К. Лекции по алгебре / Д.К. Фаддеев. М., 1984.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

алгебраическая структура, 5 специальная линейная, алгебраическое замыкание поля, 103 специальная ортогональная, базис абелевой группы, 48 циклическая, 16, групп, группа, многочленов от нескольких пере- подкольцо, симметрических многочленов, 85 поле, 55, лексикографическая запись много- полином, лексикографическое упорядочение, порядок матрица элементарная, 17 групп, мономорфизм, образ гомоморфизма, 26 расширение поля, операция алгебраическая, 5 простое, многочлена относительно перемен- Ферма, расширения полей, критерий подполя конечного поля, функция Эйлера, критерий равенства смежных клас- характеристика поля, о конечной мультипликативной примитивный конечного поля, о мультипликативности степени трансцендентный, о мультипликативности функции эпиморфизм, Эйлера, о несущественности алгебраичес- Я о согласованных базисах, 50 гомоморфизма группы, о строении конечно порожденных гомоморфизма колец, абелевых групп,

СОДЕРЖАНИЕ

Г л а в а 2. ОСНОВЫ ТЕОРИИ КОЛЕЦ И ПОЛЕЙ.

ЛЕКЦИИ ПО АЛГЕБРЕ: ГРУППЫ, КОЛЬЦА, ПОЛЯ

Учебное пособие для студентов математических специальностей Подписано в печать. Формат 6084/16. Бумага офсетная. Гарнитура «Computer Modern Roman». Печать офсетная. Усл. печ. л. 6,74. Уч.-изд. л. 6,6. Тираж 100 экз.

Белорусский государственный университет. ЛИ № 02230/0056804 от 02.03.2004.

220030, Минск, проспект независимости, 4.

Отпечатано с оригинала-макета заказчика. Республиканское унитарное предприятие «Издательский центр Белорусского государственного университета». ЛП № 02330/0056850 от 30.04.2004 220030, Минск, ул. Красноармейская, 6.

«d?3 Ф Е Д Е Р А Л Ь Н О Е А Г Е Н Т С Т В О ПО О Б Р А З О В А Н И Ю Архангельский государственный технический университет МЕТЕОРОЛОГИЧЕСКИЕ МЕТОДЫ В ЛЕСНОМ МОНИТОРИНГЕ Методические указания к лабораторным занятиям ©ailTime ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Архангельский государственный технический университет Н.Р.СУНГУРОВА, канд. с.-х. наук ; Н.А.БАБИЧ, проф., д.с.-х. наук МЕТЕОРОЛОГИЧЕСКИЕ МЕТОДЫ В ЛЕСНОМ МОНИТОРИНГЕ Методические указания к лабораторным занятиям Рассмотрены и рекомендованы. »

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ 14/16/6 Одобрено кафедрой Нетяговый подвижной состав СИСТЕМЫ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА И РЕМОНТА ВАГОНОВ Методические указания к выполнению курсового и дипломного проектов для студентов специальности 190302.65 Вагоны специализации 190302.65.01 ВАГОНОРЕМОНТНОЕ ПРОИЗВОДСТВО РОАТ Москва – 2009 С о с т а в и т е л ь — канд. техн. наук, доц. В.Е. Новиков Р е ц е н з е н т — канд. техн. наук, доц. Б.В. Смагин © Московский государственный. »

«Новые книги поступившие в библиотеку Университета машиностроения в октябре-декабре 2013 г. (ул. Б. Семеновская) 1 Общий отдел 1 006 Берновский Ю.Н. Технические условия на выпускаемую Б 513 продукцию или как написать ТУ правильно.-М. : ФорматМ, 2013.-112с. 1 экз. 2 Гуманитарные наук и 2 42 Английский язык : учебник для студ. вузов, обучающихся А 647 по укрупненной группе специальностей и направлений подготовки Инженерное дело, технологии и технические науки.-М. : КНОРУС,2014.-346с. 353 экз. 3 42. »

«С. М. Латыев, Г. В. Егоров, С. С. Митрофанов, А. М. Бурбаев, А. А. Воронин, Ю. А. Соколов КОНСТРУКТОРСКО-ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ И СРЕДСТВА ОБЕСПЕЧЕНИЯ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ОПТИКО-ЭЛЕКТРОННЫХ ПРИБОРОВ И СИСТЕМ Учебное пособие к выполнению лабораторных работ по дисциплине Конструирование и юстировка приборов и систем оптотехники Редакционно-издательский отдел Санкт-Петербургского национального исследовательского университета Санкт – Петербург информационных технологий, механики и оптики 197101. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра древесиноведения и специальной обработки древесины А.В. Дружинин Г.Г. Говоров В.В. Савина ТЕХНОЛОГИЯ КЛЕЕНЫХ МАТЕРИАЛОВ Методические указания к выполнению лабораторных работ по курсу Технология клееных материалов для студентов факультета МТД Исследование физико-химических, технологических и механических показателей карбамидоформальдегидных, фенолформальдегидных смол и клеев на их основе. »

«Федеральное агентство по образованию Томский политехнический университет А.В.Кабышев, С.Г.Обухов РАСЧЕТ И ПРОЕКТИРОВАНИЕ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ: СПРАВОЧНЫЕ МАТЕРИАЛЫ ПО ЭЛЕКТРООБОРУДОВАНИЮ Учебное пособие Томск 2005 УДК 621.311.4.658.26 Кабышев А.В., Обухов С.Г. Расчет и проектирование систем электроснабжения: Справочные материалы по электрооборудованию: Учеб. пособие / Том. политехн. ун-т. – Томск, 2005. – 168 с. В справочнике представлены материалы, необходимые для проектирования систем. »

«Санкт-Петербургский государственный университет информационных технологий, механики и оптики Учебно-методическое пособие по дисциплине Автоматизированные методы разработки архитектуры программного обеспечения Генельт А.Е., ассистент кафедры математического моделирования Санкт-Петербург 2007 УМП Автоматизированные методы разработки архитектуры ПО Оглавление Тема 1. Архитектура ПО 1.1. Проектирование архитектуры систем предметной области. 5 1.2. Составление плана реализации модели предметной. »

«Утвержден на заседании Ученого совета СПГУТД _ июня 2013 г. Председатель Ученого совета, ректор А. В. Демидов План издания учебной и научной литературы на 2 полугодие 2013 г. Форма Уров. № Авторы Название Вид издания Объем Тип изд. Тираж УГС обуч. обр. Факультет информационных технологий и машиноведения Кафедра теоретической и прикладной механики Рудая М. Р., Детали машин. Курсовое проектирование. Этапы Методические 1 Шим В. В., графического построения двухступенчатого 2.3 Все Бак. ЭИ указания. »

«Министерство образования и науки Российской Федерации СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования Санкт-Петербургский государственный лесотехнический университет им. С. М. Кирова (СЛИ) Кафедра электрификации и механизации сельского хозяйства ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ, ПОДСТАНЦИИ И СИСТЕМЫ Учебно-методический комплекс по дисциплине для студентов специальности 110302 Электрификация и автоматизация. »

«Федеральное агентство по образованию ГОУ ВПО Уральский государственный технический университет УПИ Е. Е. Барышев МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ Учебное электронное текстовое издание Подготовлено кафедрой Безопасность жизнедеятельности Научный редактор: д-р техн. наук В. С. Цепелев Методические указания к лабораторной работе № 3 по курсу Материаловедение и технология материалов. Методические указания содержат сведения о механических свойствах металлических материалов, о методах измерения. »

«База нормативной документации: www.complexdoc.ru МИНИСТЕРСТВО ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА СССР МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ПРОЕКТИРОВАНИЮ ЗЕМЛЯНОГО ПОЛОТНА НА СЛАБЫХ ГРУНТАХ ОДОБРЕНЫ ТЕХНИЧЕСКИМ УПРАВЛЕНИЕМ МИНИСТЕРСТВА ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА СССР ОРГТРАНССТРОЙ МОСКВА 1968 ПРЕДИСЛОВИЕ Настоящие Методические указания составлены ЦНИИСом и СоюздорНИИ в развитие действующих СНиП и должны служить руководством при проектировании земляного полотна железных и автомобильных дорог на участках торфяных. »

«Министерство образования Российской Федерации Сыктывкарский лесной институт (филиал) государственного образовательного учреждения высшего профессионального образования Санкт-Петербургская государственная лесотехническая академия им. С. М. Кирова КАФЕДРА МЕХАНИЗАЦИИ В АПК ТЕХНОЛОГИИ И ТЕХНИЧЕСКИЕ СРЕДСТВА В СЕЛЬСКОМ ХОЗЯЙСТВЕ Методические указания и контрольные задания для студентов специальности 311400 Электрификация и автоматизация сельского хозяйства заочной формы обучения Сыктывкар 2004. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКРОТЕХНИКИ И ОСНОВЫ ТЕОРИИ ЦЕПЕЙ Методические указания к выполнению лабораторных работ № 1, 2, 3, 4 Санкт-Петербург 2008 Составители: С.И. Бардинский, Т.Д. Браво, Г.Г. Рогачева, Л.Б. Свинолобова Рецензенты: кафедра электромеханических и робототехнических систем; канд. техн. »

«Федеральное агентство по здравоохранению и социальному развитию Российской Федерации ГОУ ВПО “Ижевская государственная медицинская академия” Росздрава СУДЕБНО-МЕДИЦИНСКАЯ ЭКСПЕРТИЗА МЕХАНИЧЕСКОЙ АСФИКСИИ Учебно-методическое пособие для студентов Ижевск 2008 УДК 340.626.1(075.8) ББК 58Я73 С 892 Составители: д.м.н., проф. В.И. Витер, к.м.н. А.Ю. Вавилов, к.м.н. В.В. Кунгурова. Рекомендовано центральным координационным методическим советом ГОУ ВПО “Ижевская государственная медицинская академия” С. »

«МИНИСТЕРСТВО ТРУДА, ЗАНЯТОСТИ И СОЦИАЛЬНОЙ ЗАЩИТЫ РЕСПУБЛИКИ ТАТАРСТАН ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НИЖНЕКАМСКИЙ НЕФТЕХИМИЧЕСКИЙ КОЛЛЕДЖ Варианты контрольной работы №1 по дисциплине Английский язык и методические рекомендации по её выполнению для студентов заочного отделения специальностей 140448 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям), 151031 Монтаж и техническая. »

«Министерство образования Российской Федерации Ивановская государственная текстильная академия Кафедра механической технологии текстильных материалов МЕТОДИЧЕСКИЕ УКАЗАНИЯ к проведению учебной практики для студентов 1 курса специальности 280500 “Технология трикотажного производства” Иваново Настоящие методические указания предназначены для студентов 1 курса технологического факультета специальности 280500 “Технология трикотажного производства”. В них приводятся содержание практики и порядок. »

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Источник