Доказать что если две прямые параллельны третьей то они параллельны

Помощь нужна. Докажите что если две прямые параллельны третьей прямой,то они параллельны. и рисунок

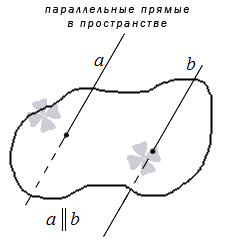
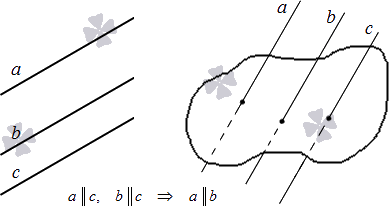
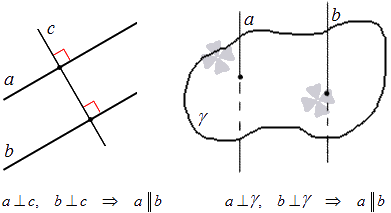
Две прямые, параллельные третьей, параллельны.
Это свойство называется транзитивностью параллельности прямых.
Доказательство
Пусть прямые a и b одновременно параллельны прямой c. Допустим, что a не параллельна b, тогда прямая a пересекается с прямой b в некоторой точке A, не лежащей на прямой c по условию. Следовательно, мы имеем две прямые a и b, проходящие через точку A, не лежащую на данной прямой c, и одновременно параллельные ей. Это противоречит аксиоме 3.1. Теорема доказана.

аксиома 3.1Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
А рисунок сам или сама, тебя не поймёшь.

Две прямые, параллельные третьей, параллельны.
Это свойство называется транзитивностью параллельности прямых.
Доказательство
Пусть прямые a и b одновременно параллельны прямой c. Допустим, что a не параллельна b, тогда прямая a пересекается с прямой b в некоторой точке A, не лежащей на прямой c по условию. Следовательно, мы имеем две прямые a и b, проходящие через точку A, не лежащую на данной прямой c, и одновременно параллельные ей. Это противоречит аксиоме 3.1. Теорема доказана.

аксиома 3.1Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
А рисунок сам или сама, тебя не поймёшь.

Источник

Планиметрия. Страница 2

1.Параллельность прямых

Теорема: если две прямые параллельны третьей прямой, то они параллельны.

Доказательство. Пусть даны две прямые а и b. Допустим, что они не параллельны между собой. (Рис.1) Тогда они пересекаются в некоторой точке С. Следовательно, через точку С проходят две прямые, параллельные прямой с. А это невозможно согласно аксиоме: через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Следовательно, прямые а и b не пересекаются. Они параллельны.

Рис.1 Теорема. Параллельность прямых.

2.Признаки параллельности прямых

Теорема. Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 градусов, то прямые параллельны.

Доказательство. Пусть даны две прямые a и b, которые образуют с секущей АВ внутренние накрест лежащие углы (Рис. 2 а). Допустим, что прямые a и b не параллельны. Тогда они пересекаются в одной точке С. Секущая АВ разбивает плоскость на две полуплоскости. И, следовательно, точка С лежит в одной из них и образует треугольник АВС. Сторона АС принадлежит прямой а. Сторона ВС принадлежит прямой b. (Рис. 2 б)

8. Пример 1

Даны прямая а и точка С, не лежащая на этой прямой. Необходимо доказать, что через точку С можно провести прямую, параллельную прямой а. (Рис.8)

Доказательство:

Проведем прямую b, параллельную прямой а. Тогда, согласно аксиоме 9, (через точку, не лежащую на данной прямой, можно провести только одну прямую) проведем прямую с через точку С, параллельную прямой b.

Таким образом, получается, что прямая с параллельна прямой b, и прямая a также параллельна прямой b по построению. Следовательно, по теореме о двух прямых, параллельных третьей прямой, имеем, что две прямые a и c параллельны прямой b и, следовательно, они (прямые а и с) параллельны. Т.е. через точку С можно провести прямую, параллельную прямой а.

Пример 2

Даны две параллельные прямые а и b, и секущая с. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных этими прямыми, параллельны (Рис.9)

Доказательство:

Таким образом, так как углы α и β равны, то и углы α/2 и β/2 также равны. А если углы α/2 и β/2 равны, то они являются внутренними накрест лежащими углами, между секущей с и прямыми, на которых лежат лучи d₁ и d₂, и согласно теореме: признак параллельности прямых, лучи d₁ и d₂ лежат на параллельных прямых.

Рис.9 Задача. Даны две параллельные прямые а и b и секущая с.

Пример 3

Один из углов равнобедренного треугольника АВС равен 100° (Рис.10). Найти остальные углы треугольника.

Решение:

Так как сумма углов треугольника составляет 180°, а два угла у равнобедренного треугольника равны, то они не могут равняться 100°. Следовательно, углы при вершинах А и С равны, а угол при вершине В = 100°.

Отсюда следует, что можно составить соотношение:

Ответ: углы равнобедренного треугольника составляют: 100°, 40°, 40°.

Рис.10 Задача. Найти углы треугольника.

Пример 4

Сумма внешних углов треугольника АВС при вершиах А и В равна 240° (Рис.11). Найдите угол С треугольника АВС.

Решение:

Так как сумма углов α + β + α₁ + β₁ = 360°, а

α₁ + β₁ = 240° по условию задачи, то

А так как сумма углов треугольника составляет 180°, то

И следовательно, γ = 60°

Ответ: угол при вершине С = 60°.

Рис.11 Задача. Найти угол треугольника.

Пример 5

В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. Угол при вершине В составляет 36° (Рис.12). Докажите, что треугольники CDA и ADB равнобедренные.

Доказательство:

Так как по условию задачи треугольник АВС равнобедренный, то углы при вершинах А и С равны:

α = 72°, а так как AD биссектриса, то ∠BAD = ∠DAC, т.е.

Следовательно, треугольник ADB равнобедренный. Углы при вершинах А и В равны 36°.

Теперь рассмотрим треугольник ADC. Угол λ равен:

Таким образом, треугольник ADC равнобедренный. Углы при вершинах С и D равны 72°.

Источник

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

Параллельность прямых

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Главная > Учебные материалы > Математика: Планиметрия. Страница 2
Рис.2 Теорема. Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых Теорема. Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны и сумма внутренних односторонних углов равна 180 градусов. Доказательство. Пусть a и b параллельные прямые. Прямая с пересекает их в точках А и В. (Рис. 3) Проведем через точку А прямую а 1 так, чтобы внутренние накрест лежащие углы, образованные между прямыми а 1 и b и секущей с, были равны. Тогда по признаку параллельности прямых они параллельны. А так как согласно аксиоме о единственной параллельной прямой, проходящей через точку не лежащей на данной прямой, такая прямая может быть только одна, то прямые а и а 1 совпадают. А следовательно внутренние накрест лежащие углы, образованные между прямыми а,b и секущей с, равны.	Рис.3 Теорема. Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника Теорема. Сумма углов треугольника равна 180 градусов. Доказательство. Пусть АВС данный треугольник. Проведем через вершину В прямую BD, параллельную стороне АС (Рис. 4). Тогда углы α и α’, γ и γ’ равны как внутренние накрест лежащие. А так как прямая BD представляет собой развернутый угол с вершиной угла в точке В, который равен 180°, т.е. α’ + β + γ’ = 180°, то сумма углов треугольника равна также 180°. Таким образом, мы пришли к выводу, что сумма углов треугольника, т.е. α + β + γ = 180°.	Рис.4 Теорема. Сумма углов треугольника. 5.Единственность перпендикуляра к прямой Теорема. Из любой точки, не лежащей на данной прямой, можно опустить только один перпендикуляр на данную прямую. Доказательство. Пусть дана прямая а и не лежащая на ней точка А. Отметим на прямой а произвольную точку, например D. И проведем через нее перпендикуляр.(Рис. 5)	Рис.5 Теорема. Единственность перпендикуляра к прямой. 6. Высота, биссектриса и медиана треугольника Высотой треугольника, проведенной из данной вершины, называется перпендикуляр, опущенный из данной вершины на противолежащую сторону. Биссектрисой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину угла и противолежащую сторону, и делящий данный угол пополам. Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину и противолежащую сторону, и делящий ее пополам. (Рис.6) Рис.6 Высота, биссектриса и медиана треугольника. 7. Свойство медианы равнобедренного треугольника Теорема. В равнобедренном треугольнике медиана, проведенная из вершины угла к основанию, является биссектрисой и высотой. Доказательство: Рассмотрим треугольники ABD и BDC. Они равны по третьему признаку равенства треугольников. АВ = ВС по условию, AD = DC, так как BD медиана, а сторона BD у них общая. Следовательно, углы при вершине D равны, а так как они являются смежными, то ∠ADB = ∠CDB = 90°. Из равенства треугольников ABD и BDC следует равенство углов при вершине В, т.е. ∠AВD = ∠CВD = α. Отсюда можно сделать вывод, что медиана BD является биссектрисой и высотой. Рис.7 Свойство медианы равнобедренного треугольника.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Ответ: AB║CD по 2 признаку параллельности прямых.

Источник