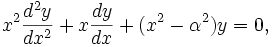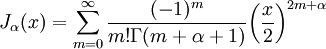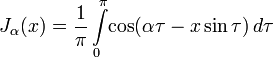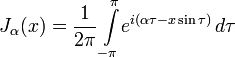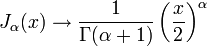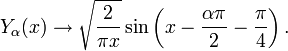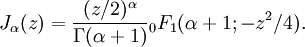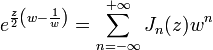Доказать что функция удовлетворяет уравнению бесселя
Доказать что функция удовлетворяет уравнению бесселя
Конкретное представление общего решения зависит от числа \(v.\) Далее мы отдельно рассмотрим два случая:
Порядок \(v\) является нецелым числом;
Порядок \(v\) является целым числом.
Примечание : В действительности общее решение дифференциального уравнения Бесселя можно выразить через функции Бесселя первого и второго рода также и для случая нецелого порядка \(v.\)
в случаях, когда объекты имеют цилиндрическую или сферическую симметрию.
Данное уравнение имеет порядок \(\sqrt 2 \) и отличается от стандартного уравнения Бесселя лишь множителем \(3\) перед \(
Это уравнение отличается от модифицированного уравнения Бесселя множителем \(4\) перед \(
Уравнение Функции Бесселя. Дифференциальное уравнение Функции Неймана
По этой ссылке вы найдёте полный курс лекций по математике:
Дифференциальным уравнением Бесселя называется уравнение вида где и — действительное число. Это уравнение имеет особую точку z = 0 (коэффициент при старшей производной в (7) обращается в нуль при х = 0). Сравнивая (5) и (7), заключаем, что для уравнения Бесселя так что х = 0 является нулем второго порядка (т = 2) функции Ро(х), нулем первого порядка функции р\(х) и не является нулем функции pi(x) (если v Ф 0).
Поэтому в силу теоремы 17 существует решение уравнения (7) в виде обобщенного степенного ряда где а — характеристический показатель, подлежащий определению. Перепишем выражение (8) в виде Уравнение Функции Бесселя Дифференциальное уравнение Г-функция Эйлера и ее свойства Рекуррентные формулы для функций Бесселя полуцелого индекса Нули бесселевых функций Ортогональность и норма Функции Неймана (Вебера) и найдем производные:
Рекуррентные формулы для функций Бесселя Используя формулу непосредственно проверкой убеждаемся в том, что Точно таким же вычислением находим Раскрывая в левых частях формул (15) и (16) производные произведений, получаем соответственно равенства Складывая и вычитая (17) и (18), получим две важные рекуррентные формулы: Формула (19) показывает, что производные функций Бесселя выражаются через бесселевы же функции.
Аналогично, при получаем Обе эти формулы можно записать в виде Уравнение Функции Бесселя Дифференциальное уравнение Г-функция Эйлера и ее свойства Рекуррентные формулы для функций Бесселя полуцелого индекса Нули бесселевых функций Ортогональность и норма Функции Неймана (Вебера) 12.6. Нули бесселевых функций При решении многих прикладных вопросов необходимо иметь представление о распределении нулей функций Бесселя.
Возможно вам будут полезны данные страницы:
Нули функций и J-x^x) совпадают с нулями sin х и cos х соответственно. Можно показать, что для больших значений х имеет место асимптотическое представление1* (сравните справедливое как для целых, так и для дробных v. Формула (22) показывает, как ведет себя функция Бесселя при возрастании аргумента. Это колеблющаяся функция, бесчисленное множество раз обращающаяся в нуль, причем амплитуда колебаний стремится к нулю при х —» +оо. Распределение нулей функции Бесселя с целым положительным индексом, т. е. корней уравнения устанавливается следующей теоремой. Теорема 18.
Функция не имеет комплексных нулей, но имеет бесконечное множество действительных нулей, расположенных симметрично относительно точки х = 0, которая в случае п = 1,2. принадлежит к их числу. Все нули функции простые за исключением точки х = 0, которая при п = 1,2. является нулем кратности п соответственно. 12.7. Ортогональность и норма функций Бесселя Ортогональность функций Бесселя Рассмотрим дифференциальное уравнение где А — некоторый числовой параметр, отличный от нуля. Нетрудно проверить, что уравнению (23) удовлетворяет функция Бесселя Jv(\x).
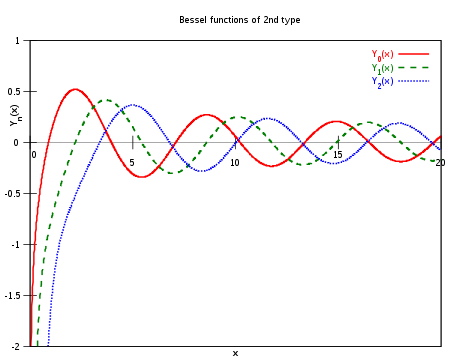
Перепишем уравнение (23) в виде и обозначим — какие-либо значения параметра А. Тогда будем иметь тождества Умножая первое тождество на ), второе — ) и вычитая одно из другого, получим Умножив все члены последнего тождества на ж, замечаем, что его можно записать в виде Интегрируя последнее тождество по ж в пределах от 0 до 1, будем иметь равенства (25) следует, что если Ai, Аг есть нули функции то левая часть (25), а значит, и правая, равны нулю, так что Это означает, согласно определению, что функции ортогональны с весом р(х) = х на отрезке [0,1). Бесселева функция Jv При v нецелом функции образуют функциональную систему решений уравнения Бесселя (7). При и = п — целом имеет место линейная зависимость Чтобы к решению Jr\x) подыскать такое, которое ему не пропорционально, поступаем так: при нецелом и составляем функцию Она является линейной комбинацией решений линейного однородного уравнения (7) и, следовательно, сама есть решение этого уравнения. Переходя в (30) к пределу при v —» п и пользуясь правилом Лопиталя, будем иметь Характерное свойство функций J/y\(х) (функций Бесселя 2-го рода) — наличие особенности в начале координат (рис. 5) Найдите решение задачи Коши: Проинтегрируйте уравнения, найдя, где указано, частные решения: Найдите общие решения следующих линейных неоднородных дифференциальных уравне- Виды частных решений неоднородных линейных уравнений с постоянными коэффициентами для различных правых частей Правая часть*) дифференциальных уравнений Корни характеристического уравнения Виды частного решения 1. Число 0 не является корнем характеристического уравнения Число 0 — корень характеристического уравнения кратности г 2. Число а не является корнем характеристического уравнения Число а является корнем характеристического уравнения кратности г 3. Числа ±»’/3 не являются корнями характеристического уравнения Числа ±«/9 являются корнями характеристического уравнения кратности г 4. Числа а ± i/З не являются корнями характеристического уравнения Числа a ± i/З являются корнями характеристического уравнения кратности г *) Первые три вида правых частей являются частными случаями четвертого. Укажите вид частных решений следующих линейных неоднородных уравнений: Методом вариации постоянных проинтегрируйте следующие уравнения: Проинтегрируйте следующие уравнения Эйлера: Ответы Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α — произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя — функции целых порядков. Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя. Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например: Функции Бесселя применяются и в решении других задач, например, при обработке сигналов. Поскольку приведённое уравнение является уравнением второго порядка, у него должно быть два линейно независимых решения. Однако в зависимости от обстоятельств выбираются разные определения этих решений. Ниже приведены некоторые из них. Здесь Γ(z) — это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально Ниже приведены графики Jα(x) для α = 0,1,2 : Если α не является целым числом, функции Jα(x) и J − α(x) линейно независимы и, следовательно, являются решениями уравнения. Но если α целое, то верно следующее соотношение: Оно означает, что в этом случае функции линейно зависимы. Тогда вторым решением уравнения станет функция Бесселя второго рода (см. ниже). Этот подход использовал Бессель, изучив с его помощью некоторые свойства функций. Возможно и другое интегральное представление: Для функций Бесселя известны асимптотические формулы. При маленьких аргументах где γ — постоянная Эйлера — Маскерони (0.5772…), а Γ — гамма-функция Эйлера. Для больших аргументов ( Функции Бесселя могут быть выражены через гипергеометрическую функцию: Таким образом, при целых n функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая. Существует представление для функций Бесселя первого рода и целого порядка через коэффициенты ряда Лорана функции определённого вида, а именно функция Бесселя — Beselio funkcija statusas T sritis fizika atitikmenys: angl. Bessel function vok. Bessel Funktion, f rus. функция Бесселя, f pranc. fonction de Bessel, f … Fizikos terminų žodynas Функция Ломмеля — Функция Ломмеля неэлементарная функция, которая является частным решением неоднородного уравнения Бесселя: Введена немецким математиком Эйгеном фон Ломмелем.[1][2] Интегральное выражение функции Ломмеля: где … Википедия Функция Неймана — Функции Бесселя в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия Бесселя функции — Функции Бесселя в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где α произвольное действительное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия Функция Ангера — неэлементарная функция, которая является частным решением неоднородного уравнения Бесселя: Интегральное выражение функции Ангера: где функция Бурже. При целых функция Ангера совпадает с функцией Бе … Википедия Функция sinc(x) — Функция sinc(x) … Википедия Функция Струве — Функция Струве неэлементарная функция, которая является частным решением неоднородного уравнения Бесселя: Интегральное выражение функции Струве: Разложение в ряд … Википедия БЕССЕЛЯ УРАВНЕНИЕ — линейное обыкновенное дифференциальное уравнение 2 го порядка: илц в самосопряженной форме: Число v наз. индексом Б. у.; величины в общем случае могут принимать комплексные значения. После подстановки получается приведенная форма уравнения (1): Б … Математическая энциклопедия Поскольку это линейное дифференциальное уравнение второго порядка, должно быть два линейно независимых решения. Однако в зависимости от обстоятельств удобны различные составы этих растворов. Различные варианты приведены в таблице ниже и описаны в следующих разделах. Для нецелого числа α функции J α ( x ) и J — α ( x ) линейно независимы и, следовательно, являются двумя решениями дифференциального уравнения. С другой стороны, для целого порядка n справедливо следующее соотношение (гамма-функция имеет простые полюсы у каждого из неположительных целых чисел): [4] Это означает, что два решения больше не являются линейно независимыми. В этом случае второе линейно независимое решение оказывается функцией Бесселя второго рода, как обсуждается ниже. Другое определение функции Бесселя для целых значений n возможно с использованием интегрального представления: [5] Другое интегральное представление: [5] Это был подход, который использовал Бессель, и из этого определения он вывел несколько свойств функции. Определение может быть расширено до нецелочисленных порядков с помощью одного из интегралов Шлефли для Re ( x )> 0 : [5] [6] [7] [8] [9] Функции Бесселя могут быть выражены в терминах обобщенного гипергеометрического ряда как [10] В терминах полиномов Лагерра L k и произвольно выбранного параметра t функция Бесселя может быть выражена как [11] В случае целочисленного порядка n функция определяется путем взятия предела, когда нецелое число α стремится к n : Также существует соответствующая интегральная формула (при Re ( x )> 0 ): [15] Более того, когда α является целым числом, как это было аналогично для функций первого рода, справедливо следующее соотношение: Функции ганкелевы используются для выражения outward- и внутрь распространяющихся цилиндрической волна решения уравнения цилиндрической волны, соответственно (или наоборот, в зависимости от знака конвенции по частоте ). Используя предыдущие отношения, их можно выразить как Если α является целым числом, необходимо вычислить предел. Следующие отношения действительны, независимо от того, является ли α целым числом или нет: [17] Они полезны при разработке сферических функций Бесселя (см. Ниже). Функции Ганкеля допускают следующие интегральные представления при Re ( x )> 0 : [18] где пределы интегрирования указывают на интегрирование по контуру, который можно выбрать следующим образом: от −∞ до 0 вдоль отрицательной действительной оси, от 0 до ± πi вдоль мнимой оси и от ± πi до + ∞ ± πi вдоль контура, параллельного к реальной оси. [15] K α = < π 2 i α + 1 H α ( 1 ) ( i x ) − π arg x ≤ π 2 π 2 ( − i ) α + 1 H α ( 2 ) ( − i x ) − π 2 arg x ≤ π <\displaystyle K_<\alpha >=<\begin x 2 d 2 y d x 2 + x d y d x − ( x 2 + α 2 ) y = 0. <\displaystyle x^<2><\frac Глава I. Дифференциальное уравнение Бесселя и его интегралы .1 Дифференциальное уравнение Бесселя с дробным индексом .2 Дифференциальное уравнение Бесселя с целым индексом .2.1 Бесселевы функции третьего рода .3 Бесселевы функции мнимого аргумента .4 Рекуррентные формулы для бесселевых функций .5 Бесселевы функции, индекс которых равен целому числу с половиной .6 О корнях бесселевых функций .7 Интеграл Бесселя .8 Интеграл Пуассона .9 Применение теоремы Коши к интегралу Пуассона 1.10 Асимптотическое представление при больших значениях аргумента .11 Асимптотические формулы бесселевых функций Глава II. Некоторые применения функций Бесселя .1 Бесселевы функции в астрономии .2 Приложение к теории продольного изгиба 2.3 Приложение к теории гармонических функций 2.4 Пример задачи на тепловое равновесие .5 Тепловое равновесие бесконечного цилиндра .6 Обобщение прежнего примера .7 Задача из электростатики 2.8 Разложение по бесселевым функциям 2.9 Дифференциальное уравнение второго порядка Одним из первых приложений Бесселевых функций, наличие которого значительно содействовало появлению и развитию теории этих функций, был вопрос об эллиптическом движении планет. Ряды, полученные Бесселем, позволили изучать движение комет с такой же легкостью, как и планет. Современная теория Бесселевых функций-результат длинного ряда работ многих ученых, в том числе таких крупных, как Пуассон, Якоби, Куммер, Риманн, Ганкель и др. Из русских ученых много занимались Бесселевыми функциями академик Сонин, Динник и Адамов. Одно совсем неожиданное приложение Бесселевых функций к самым высоким областям теории чисел открыл замечательный русский математик Г. Ф. Вороной. Цилиндрическими функциями называются решения линейного дифференциального уравнения второго порядка Термин «цилиндрические функции» обязан своим происхождением тому обстоятельству, что уравнение (1) встречается при рассмотрении краевых задач теории потенциала для цилиндрической области. Специальные классы цилиндрических функций известны в литературе под названием функций Бесселя, и иногда это наименование присваивается всему классу цилиндрических функций. Хорошо разработанная теория рассматриваемых функций, наличие подробных таблиц и широкая область применений служат достаточным основанием для того, чтобы отнести цилиндрические функции к числу наиболее важных специальных функций. Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например: 1) электромагнитные волны в цилиндрическом волноводе; 2) теплопроводность в цилиндрических объектах; ) формы колебания тонкой круглой мембраны; ) скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси. Функции Бесселя применяются и в решении других задач, например, при обработке сигналов. Цилиндрические функции Бесселя являются самыми распространенными из всех специальных функций. Они имеют многочисленные приложения во всех естественных и технических науках (особенно в астрономии, механике и физике). В ряде задач математической физики встречаются цилиндрические функции, в которых аргумент или индекс (иногда и тот и другой) принимают комплексные значения. Для численного решения таких задач необходимо разработать алгоритмы, позволяющие вычислять функции Бесселя с высокой точностью. Объектом исследования является решение дифференциальных уравнений. Предметом исследования являются цилиндрические функции Бесселя. Целью данной выпускной квалификационной работы является изучение функций Бесселя и применение их свойств в решении дифференциальных уравнений. 1) Изучить уравнение Бесселя и его интегралы: дифференциальное уравнение Бесселя с дробным индексом, дифференциальное уравнение Бесселя с целым индексом, бесселевы функции третьего рода, бесселевы функции мнимого аргумента, рекуррентные формулы для бесселевых функций, бесселевы функции, индекс которых равен целому числу с половиной, о корнях бесселевых функций, интеграл Бесселя, интеграл Пуассона, применение теоремы Коши к интегралу Пуассона, асимптотическое представление при больших значениях аргумента, асимптотические формулы бесселевых функций. ) Рассмотреть некоторые применения функций Бесселя: бесселевы функции в астрономии, приложение к теории продольного изгиба, приложение к теории гармонических функций, пример задачи на тепловое равновесие, тепловое равновесие бесконечного цилиндра, задача из электростатики, разложение по бесселевым функциям. ) Решить дифференциальное уравнение второго порядка с использованием функции Бесселя. Структура и объем работы. ВКР состоит из введения и двух глав, заключения, списка использованной литературы. Текст изложен на 70 страницах. Список литературы содержит 12 наименований. Глава I. Дифференциальное уравнение Бесселя и его интегралы 1.1 Дифференциальное уравнение Бесселя с дробным индексом Решение многих вопросов приводится к интегрированию дифференциального уравнения цилиндрическая бесселева функции дифференциальный В этом параграфе мы займемся отысканием интегралов при n дробном. Случай, когда n целое число, оказывается более трудным и будет рассмотрен в дальнейшем. При n произвольном не удается найти элементарную функцию, удовлетворяющую уравнению (1). Поэтому Бесселевы функции являются новыми функциями, не выражающимися через элементарные. В самом деле уравнение (1) имеет вид: В правой части знаменатель при х = 0 обращается в нуль. В виду сказанного ищем решение уравнения (1) в форме степенного ряда более общего вида, чем ряд (3), а именно полагаем: Здесь какое-нибудь число, может быть целое, может быть и дробное или отрицательное. Ясно, что при дробном, по крайней мере, одна из производных и обращается в при х=0. При отрицательном сама функция и обращается в бесконечность при х = 0. Дифференцируя равенство 4) два раза, находим вместе с ним три равенства: После этого получаем равенство: Таким образом находим ряд уравнений, которые по упрощении можно написать так: Подставляя эти данные в равенство (4), находим: Тогда функция u, определяемая равенством (8), превращается в функцию Бесселя, обозначаемую (х). Равенство (8) можно будет после этого переписать в таком виде: Раскрыв скобки и воспользовавшись основным свойством Гамма-функции, это равенство можно переписать еще в такой форме: Если n число дробное, то оба числа и отличны от нуля, так как только в том случае, когда s равно нулю или целому отрицательному числу. Поэтому разложение (10) и (11) начинаются с разных степеней х и, следовательно, функции и линейно независимы, т. е. одна из них не получается из другой помножением на некоторую постоянную. Таким образом при n дробном можем написать общий интеграл уравнения Для и можно составить таблицы их значений, пользуясь рядами (10) и (11) и некоторыми другими, которые выведем в дальнейшем и которые удобны при больших значениях х. 1.2 Дифференциальное уравнение Бесселя с целым индексом При n целом две функции и оказываются линейно зависимыми друг от друга и формулы (12) уже не дает общего интеграла уравнения Бесселя. В самом деле, если n целое положительное число, то в правой части формулы (11) § 1 коэффициенты при n первых слагаемых обращаются в нуль в силу равенств: Поэтому формула (11) § 1 принимает такой вид: Поэтому равенство (1) после упрощения становится таким: Сравнивая это с равенством (10) предыдущего параграфа, находим: Таким образом функции и при целом n линейно зависимы, как было сказано. Для получения общего интеграла дифференциального уравнения Бесселя удобно исходить из других частных интегралов. Все они получаются из формулы (12) § 1. Если в ней придать постоянным и какие-нибудь специальные значения, то получится один из частных интегралов уравнения (1). Различные авторы получали таким образом различные Бесселевы функции. В частности, например, если взять то получится функция введенная Вебером (1873 г.). Таким образом функция Вебера определяется при n дробном равенством: При n целом принимает неопределенный вид. В самом деле, знаменатель тогда очевидно обращается в нуль, а числитель превращается в величину: , которая равна нулю в силу равенства (2). Можно однако раскрыть эту неопределенность, найдя величину предела дроби в правой части равенства (3) при n стремящемся к целому числу. Для этого проще всего применить правила Лопиталя, согласно которому, если при х = а числитель и знаменатель дроби обращаются в нуль, то при условии, что правая часть имеет смысл и что непрерывая при x=a. В данном случае переменная в равенстве (3) обозначена через n, поэтому при n целом получаем: Выполняя дифференцирования, находим: Так как sin = 0, a cos n = при целом n, то получаем для целых значений n: Величины и легко вычислить. Так, например, имеем: Таким же образом находим: Пользуясь равенством (2) и выделяя в сумму те слагаемые, у которых В первой сумме слагаемые можно преобразовать, исходя из формулы: Следовательно при имеем: Поэтому первая из сумм превратится в такую: Вторая сумма в формуле (7) может быть упрощена, если положить v = n+k После этого она принимает вид: Подставляя результаты (5), (7), (8) и (9) в равенство (4), получим: При этом значок k в равенстве (9) переименован в v и слагаемые этой суммы объединены со слагаемыми суммы равенства (5). Пользуясь формулой: справедливой при целом s, равенство (10) можем переписать в таком виде: Полученная функция удовлетворяет такому же уравнению, но при целом n. С помощью функции Вебера общий интеграл уравнения Бесселя может быть написан в такой форме: носит название функции Бесселя второго рода. 1.2.1 Бесселевы функции третьего рода Хотя общий интеграл уравнения Бесселя может быть выражен через функции (x) и (x), но в некоторых вопросах удобнее употреблять некоторые другие интегралы уравнения Бесселя. На основании теории линейных дифференциальных уравнений эти интегралы должны быть линейными комбинациями функций (x) и (x). Эти функции, как это видно из их определения, имеют мнимые значения при вещественных значениях х. Так как (x) можно выразить через (x) и (x), то и функции Ганкеля можно выразить через те же величины. При этом получаются формулы: Эти функции справедливы и при целом n, если в правой части ставить предел, к которому она стремится при приближении n к данному целому числу. 1.3 Бесселевы функции мнимого аргумента Разлагая в ряд, получаем: (х) удовлетворяет дифференциальному уравнению, которое тоже можно назвать Бесселевым и которое получается из прежнего заменой переменных. Оно имеет вид:+x. (2) 1.4 Рекуррентные формулы для Бесселевых функций Между тремя функциями Бесселя индексы которых отличаются на единицу, существует простая линейная зависимость. Ее легко получить исходя из разложения этих функций в ряды: Согласно формуле (10) § 1 имеем по замене n на n-1 и n+1 два равенства: Складывая почленно (1) и (2), находим: Если вычесть равенство (2) из равенства (1), то подобным же образом получится: Правая часть очевидно равняется величине 2. Следовательно: Рекуррентным формулам можно придать и иной вид. Так нетрудно проверить, пользуясь рядами, подобно предыдущему, две следующие весьма простые формулы: Исходя из определений, нетрудно проверить, что и для этих функций справедливы соответствующие рекуррентные формулы. Так, например, имеем: 1.5 Бесселевы функции, индекс которых равен целому числу с половиной Рассмотрим простейший случай n=В этом случае имеем Величины Гамма-функций, имеющиеся в знаменателе, находятся по формулам, данным в § 1 первой главы: Подставляя это в равенство (1) после упрощений найдем: Подобным же образом доказывается равенство: Поэтому при n равном целому числу с половиной функции Бесселя могут быть выражены через элементарные функции. Например при k целом положительном с помощью рекуррентных формул можно доказать справедливость равенства: Точно так же с помощью рекуррентных формул можно доказать справедливость равенства, дающего при целом k значение функции в развернутом виде: Здесь для краткости введены обозначения: При этом n=k+ и в обоих случаях суммирование продолжается до появления в числителе множителей, обращающихся в нуль. Для функции существует аналогичная формула, только в ней тригонометрические функции и заменяются гиперболическими. Путь доказательства равенства (5) таков. Сначала проверяется, что при k=-1 и +1 формула (5) дает верные результаты. Затем доказывается, что функция, определяемая правой частью (5), удовлетворяет таким же рекуррентным формулам, как и (x). Сопоставление этих результатов приводит к доказательству того, что (5) верно всегда при любом целом k. 1.6 О корнях Бесселевых функций В дальнейшем мы увидим, что при вещественном значении n каждая функция Бесселя имеет бесчисленное множество вещественных корней. Теперь мы рассмотрим некоторые свойства этих корней. Для этого следует предварительно сделать несколько замечаний. Первое из них состоит в следующем. Пусть даны u и v интегралы двух линейных дифференциальных уравнений: Помножая первое из этих уравнений на v, а второе на u и вычитая их друг от друга, находим: Это уравнение можно переписать и так: Интегрируя в пределах а и b это равенство, получаем: Второе замечание состоит в следующем: уравнение Бесселя удовлетворяют уравнениям вида (1), а именно: Применяя сюда равенство (2), при a=0, b=1 имеем: Выражая здесь производные от бесселевой функции через саму функцию с помощью рекуррентных формул и подставляя пределы интегрирования, находим: Известно, как важна роль равенств (10) в теории рядов Фурье. Подобное же значение имеет равенство (9) при разложении функций в ряды по бесселевым функциям, к которым приводят некоторые задачи математической физики. Более глубокие сведения о корнях Бесселевых функций можно получить на основании результатов дальнейших параграфов. В частности, как будет показано в дальнейшем, функция при больших значениях х приближенно может быть представлена в виде равенства: 1.7 Интеграл Бесселя При целых значениях числа n функция может быть представлена в виде особого определенного интеграла, найденного Бесселем. К нему можно придти исходя из следующей задачи. Функция четная функция относительно обладает периодом 2. Согласно теории рядов Фурье она должна раскладываться в ряд Фурье, расположенный по косинусам кратных углов, а именно должно быть справедливо равенство: где коэффициенты определяются формулой: Непосредственно вычислить этот интеграл затруднительно. Можно избрать другой путь для нахождения коэффициентов. Замечая, что Удовлетворить этому равенству легко. Для этого пишем: Сравнивая полученное равенство с (3) и (2), находим: Заметим, что по свойству интегралов от четных и нечетных функций справедливы равенства: Помножив второе на и сложив с первым, получим после подстановки полученного в (9): С помощью равенства уравнение (10) можно написать так: Так как подинтегральная функция периодическая, то вместо пределов интегрирования можно взять любые числа, лишь бы они тоже отличались друг от друга на 2. Поэтому можем написать: Последнее можно переписать еще и так: Это и есть интеграл, найденный Бесселем. Предыдущий вывод существенно предполагает, что n целое число. При n нецелом формула (14) становится неверной и должна быть заменена другой, получающейся более сложным путем. Она имеет такой вид: 1.8 Интеграл Пуассона Для изучения свойств Бесселевых функций имеет большое значение другое интегральное представление их, открытое Пуассоном. Оно может быть получено, исходя из разложения этих функций в степенной ряд, т. е. из равенства: Умножим числитель и знаменатель общего члена ряда Г( и воспользуемся формулой (6) § 8 гл. I, которая при s=, получает вид: После этого общий член ряда принимает вид: Последнее же очевидно равно такому выражению: Последний множитель есть не что иное, как функция B (p,q) при Поэтому, если воспользоваться выражением B (p,q)= B (q,p) в виде определенного интеграла, то величина (3) принимает вид: Полагая и подставляя преобразованную величину (4) в равенство (1), находим: Здесь можно переставить суммирование и интегрирование. После этого под знаком интеграла получится величина Поэтому равенство (5) преобразуется в такое: По свойству интегралов от четных функций его можно переписать и так: Ясно, что интегралы (6), (7) и (8) имеют смысл только при том условии, что n+> 0, иначе они не будут сходящимися, так как при t или величины или будут стремиться к быстрее, чем это следует для сходимости. 1.9 Применение теоремы Коши к интегралу Пуассона С помощью теоремы Коши об интегралах от функций комплексного переменного можно получить из интеграла Пуассона еще одно интегральное представление, весьма важное для теории функций Бесселя. Для этого прежде всего следует интеграл в равенстве (7) § 8 переписать иначе, выразив с помощью формулы Эйлера cos tx через показательную функцию. Таким образом получаем: Изучим первый интеграл. Для этого введем положительные числа N и p, из которых N будем в дальнейшем увеличивать до бесконечности, а p, и применим теорему Коши. За подинтегральную функцию возьмем Интегрируя это уравнение, находим: Интегрируя его, получаем: Полученное уравнение похоже на уравнение, которому удовлетворяет функция : После подстановки в уравнение (19) находим: Найдя R, Ф и Z и перемножив их, получаем частный интеграл уравнения Лапласа. При этом величина коэффициентов совершенно произвольно, а число m может быть произвольным целым числом. Таким образом предыдущее дает возможность находить бесчисленное множество частных интегралов уравнения Лапласа. Помножая их на произвольные постоянные и складывая, найдем более общий интеграл. Располагая выбором множества произвольных постоянных и, следовательно, имея возможность выбирать из большого множества интегралов, Можем рассчитывать найти и тот интеграл, который отвечает данной задаче. Примеры этого рассмотрим в следующих параграфах. 1.4 Пример задачи на тепловое равновесие Пусть требуется определить установившееся распределение температуры в пространстве между двумя плоскостями: и и расположенного снаружи от цилиндра, ось которого расположена по оси OZ, а радиус равен единице. При этом будем предполагать, что в верхней и нижней плоскости поддерживается температура равная нулю, а на поверхности цилиндра температура поддерживается на постоянном уровне t. Таким образом там u = t. Согласно предыдущему его частный интеграл может быть представлен в форме: RZ, где R зависит только от Rr, a Z содержит только координату z. При этом Z и R должны удовлетворять уравнению (7) и (12) т. е. уравнениям В данном случае положено в этих уравнениях b = 0, так как при этом получается Ф = const. Пользуясь ими, составляем произведение RZ и находим такие частные решения для u, равного RZ: На основании теории линейных уравнений можем из частных интегралов и получить множество новых интегралов, помножая на произвольные постоянные и складывая. Таким образом находим интеграл и уравнения (1) в весьма общей форме: Это равенство похоже на разложение функции в ряд Фурье. Если выбрать постоянные соответствующим образом, то оно и будет этим разложением. Из теории рядов Фурье известно, что любая функция f(x), удовлетворяющая условиям весьма общего характера, разлагается в ряд Фурье: При этом коэффициенты и определяются равенствами: В случае, если четная функция, т. е. то тогда эти формулы можно заменить такими: Разложение имеет вид: Упрощая (12), находим, что при имеет место равенство: Подставляя найденные результаты в равенство (5), находим: Функция u, представляемая рядом (15), выполняет все условия задачи. В самом деле, благодаря убыванию функции при больших значениях аргумента ряд (15) при r, т. е. вне цилиндра сходится, и может быть дважды дифференцируем. Поэтому его сумма остается гармонической функцией от r и z подобно ее слагаемым. Кроме того при r= 1 равенство (15) обращается в справедливое тождество (13). Наконец на плоскостях н при находим: u = 0 в силу равномерной сходимости ряда и того обстоятельства, что при имеем: Если в формуле (15) заменим функцию на то получится решение задачи распределения температуры внутри цилиндра, на боках которого температура равна t, а на основаниях равна нулю: При этом ряды (15) и (16) будут быстро сходящимися, если величина r не близка к единице. Например из (16) при z = 0, r=0 находим: Ограничиваясь одним первым членом, получаем: Дальнейшие члены ряда (18) весьма малы в силу быстрого возрастания знаменателей. Так при k = 1 находим: 2.5 Тепловое равновесие бесконечного цилиндра Иначе говоря, имеем: В частности если т. е. если четная функция, то формула (3) может быть написана в более простом виде: Если же т. е. нечетная, то Например в данной задаче участвует функция Согласно формуле Фурье (4) она может быть представлена в таком виде: На первый взгляд формула Фурье может показаться весьма непрактичным превращением простой величины, например в сложный вид двойного интеграла. Однако, как увидим сейчас, это не совсем так. Из равенства (2) и свойства линейных уравнений вытекает, что и функции такого вида: Лаплас доказал, что Поэтому окончательно находим: Эта формула дает возможность вычислить температуру в любой точке внутри цилиндра. Вычисление интеграла не представляет затруднений. В самом деле, в виду того, что возрастающая функция, имеем неравенство: Далее находим: 2.6 Обобщение прежнего примера Только что рассмотренный пример есть частный случай задачи, известной в теории гармонических функций под именем задачи Дирихле. Она состоит в отыскании гармонической функции, принимающей на данной поверхности заданные значения. Если поверхность замкнутая, то задача Дирихле определенная. В данном случае поверхность была бесконечный незамкнутый цилиндр. Здесь задача имеет бесчисленное множество решений. Если однако искать только такие функции, которые остаются конечными при беспредельном возрастании |z|, то задача имеет только одно решение. Это доказано автором данной книги. В формуле (1) коэффициенты и можно выразить с помощью интеграла Фурье. Тогда она примет такой вид: Таким образом окончательный ответ оказывается таким: Полученный ответ на первый взгляд может показаться чрезмерно сложным. Однако и сама задача Дирихле достаточно сложна. Например, если дело идет о тепловом равновесии, то температура внутри цилиндра должна зависеть от температуры всех точек поверхности. Последняя может меняться вдоль по поверхности весьма прихотливым образом. Формула должна учесть взаимодействие всех этих, быть может, очень сложных влияний, и нет основания думать, что существует возможность охватить всю сложность действительности простым образом. Следующий пример имеет целью показать, что формула (4) и аналогичная ей при всей своей внешней сложности достаточно проста, чтобы допустить фактическое вычисление интересующей нас величины. 2.7 Задача из электростатики Предположим, что цилиндр радиуса равный единице соединен с землей и потенциал его таким образом нуль. На поверхности цилиндра выделен с помощью изоляции участок, ограниченный с боков двумя образующими, а сверху и снизу двумя полукругами (рис. 4). Выделенный участок поверхности цилиндра ABDCEF имеет потенциал единица. При этом, положим, дано Ag = gF =1. Требуется найти потенциал в любой точке снаружи от цилиндра. В данном случае поступаем, следуя пути, указанному в предыдущем параграфе. Функция определяется теперь условиями: )при величина =1, если и равна нулю, если лежит в одном из интервалов Разлагаем в ряд Фурье. При находим: При этом функция четная относительно и коэффициенты и определяются формулами: Таким образом находим: Здесь при (z) и в противном случае. Величину можно представить интегралом Фурье. Согласно (4) § 5 находим: Равенство (3) после замены интегралом (4) получает вид: Если решать вопрос о распределении потенциала внутри цилиндра, то функции K должны быть заменены функциями I. Потенциал u будет выражаться равенством: Интегралы в формулах (6), (7), (8) могут быть легко вычислены приближенно в виду быстрого уменьшения подинтегральной функции. Благодаря этому интеграл до бесконечности может быть заменен интегралом до конечного и не очень большого предела, а последний может быть вычислен, например, по формуле Симпсона. При этом оказывается, что величины этих интегралов с возрастанием 2k+1 быстро уменьшаются. Поэтому достаточно взять немного членов бесконечного ряда, чтобы получить значительную точность. Сказанное будет особо справедливо при больших r в формулах (6) и (7). В формуле (8) при r близких к нулю сходимость будет однако медленная. Определение u при r=0 непосредственно по формуле (8) невозможно и требует довольно сложных дополнительных исследований. 2.8 Разложение по Бесселевым функциям В виде примера еще одного способа применения Бесселевых функций рассмотрим задачу об установившемся распределении тепла в бесконечном цилиндре круглого сечения, опирающемся основанием на плоскость XOY. При этом ось симметрии цилиндра примем за ось OZ (рис. 5). Для простоты решения ограничимся простейшим случаем, а именно будем считать, что на боковой поверхности поддерживается температура, равная нулю, а на основании цилиндра температура и зависит только от расстояния r до оси цилиндра u=f(r). Радиус цилиндра примем за единицу. Согласно § 3 дело сводится к нахождению того интеграла уравнения Лапласа, который удовлетворяет данным условиям на поверхности. По прежнему в основу решения кладется метод частных решений. На основании изложенного в том же параграфе, одно из решений уравнения Лапласа имеет вид: K,,Z, где К, Ф, Z функции от r, и z соответственно, удовлетворяющие условиям: Дальше полезно воспользоваться свойствами ортогональности Бесселевых функций (см. гл. I, § 6): Помножая равенство (5) на и интегрируя в пределах от 0 до 1, находим: Вследствие формулы (6) все интегралы в правой части равенства (7) обращаются в нуль за исключением одного при n = m. Определив отсюда и подставив результат в (5) находим: Это равенство дает разложение функции f(r), в ряд, расположенный по Бесселевым функциям. Это разложение по своему выводу и по своей общности напоминает разложение функций в ряд Фурье и поэтому часто называется разложением Фурье- Бесселя. Приведенное рассуждение не вполне полно, но более подробное исследование показывает верность равенства (9) в весьма широком классе случаев. Подставляя величины коэффициентов в равенстве (4), получим ответ на задачу. 2.9 Дифференциальное уравнение второго порядка Решить дифференциальное уравнение: В данном уравнении сделаем замену Подставим найденные производные в исходное уравнение, получим:Записав левую часть равенства (25) Функция Бесселя
Содержание
Применения
Определения
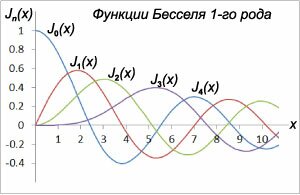
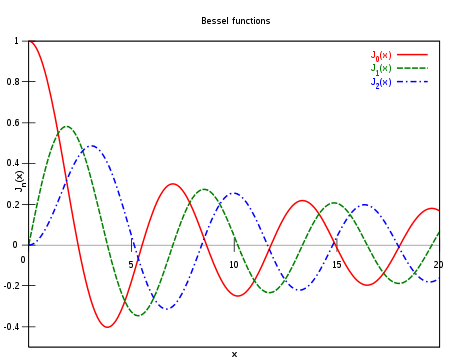
Функции Бесселя первого рода
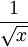
Интегралы Бесселя
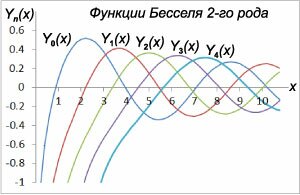
Функции Бесселя второго рода
Свойства
Асимптотика
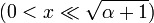

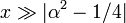
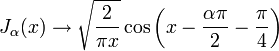
Гипергеометрический ряд
Производящая функция
См. также
Литература
Полезное
Смотреть что такое «Функция Бесселя» в других словарях:
Функция Бесселя
СОДЕРЖАНИЕ
Приложения функций Бесселя [ править ]
Определения [ править ]
Функции Бесселя первого рода: J α [ править ]
Интегралы Бесселя [ править ]
Отношение к гипергеометрическим рядам [ править ]
Связь с полиномами Лагерра [ править ]
Функции Бесселя второго рода: Y α [ править ]
Доказать что функция удовлетворяет уравнению бесселя