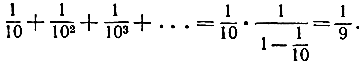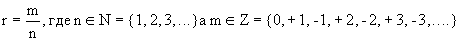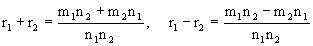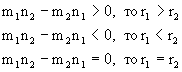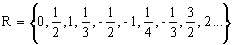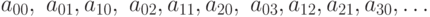Доказать что множество рациональных чисел счетно

Доказать что множество рациональных чисел счетно

2. Счетность множества рациональных чисел и несчетность континуума

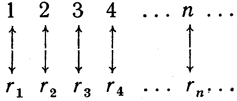
Одно из первых открытий Кантора в области анализа бесконечного заключалось в том, что множество рациональных чисел (содержащее в качестве правильного подмножества бесконечное множество натуральных чисел и потому само бесконечное) эквивалентно множеству натуральных чисел. На первый взгляд кажется странным, что всюду плотное множество рациональных чисел не более богато элементами, чем множество натуральных чисел, элементы которого «рассеяны» редко и стоят на значительном расстоянии один от другого. И в самом деле, с сохранением порядка возрастания нельзя расположить положительные рациональные числа так, как это можно сделать с натуральными: самое маленькое число а будет первым, следующее за ним по величине b вторым и т. д.; дело в том, что рациональные числа расположены всюду плотно, и потому ни для одного из них нельзя указать «следующего по величине». Но Кантор заметил, что если отказаться от требования «располагать по величине», то тогда оказывается возможным расставить все рациональные числа в ряд r₁, r₂, r₃, r₄. подобный ряду натуральных чисел. Такое расположение предметов некоторого множества в виде последовательности часто называют пересчетом («нумерацией») этого множества. Множества, для которых пересчет может быть выполнен, называются счетными или исчислимыми. Указывая один из способов пересчета множества рациональных чисел и устанавливая, таким образом, его счетность, Кантор тем самым показал, что это множество эквивалентно множеству натуральных чисел, так как

схема создает взаимно однозначное соответствие между двумя множествами. Мы опишем сейчас один из возможных способов пересчета множества рациональных чисел.

Рис. 19. Пересчет рациональных чисел

Если мы выбросим теперь все дроби, у которых числитель и знаменатель имеют отличные от 1 общие делители, то останется последовательность, в которой каждое рациональное число встретится в точности один раз:

Так устанавливается, что множество всех рациональных чисел является счетным. Принимая во внимание, что рациональные числа взаимно однозначно связаны с рациональными точками числовой прямой, можно также сказать, что множество рациональных точек на числовой прямой счетно.

Упражнения. 1) Покажите, что множество всех целых, положительных и отрицательных чисел счетно. Покажите, что множество всех рациональных, положительных и отрицательных чисел счетно.

2) Покажите, что если S и Т- счетные множества, то множество S + Т (см. стр. 138) также счетно. То же покажите для суммы трех, четырех и, вообще, n множеств; покажите, наконец, что множество, составленное посредством сложения счетного множества счетных множеств, также счетно.

Однако проведем это рассуждение фактически. Допустим, что все действительные числа, представленные в виде бесконечных десятичных дробей, расположены в виде последовательности, или списка:

где буквы N_i обозначают целую часть, а буквы а, b, с. представляют собой десятичные знаки, стоящие вправо от запятой. Мы допускаем, что эта последовательность дробей охватывает все действительные числа. Существенной частью доказательства является построение с помощью «диагональной процедуры» такого нового числа, относительно которого можно показать, что оно не входит в наш список.

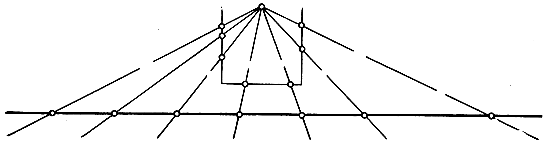
Рис. 20. Взаимно однозначное соответствие между точками согнутого интервала и точками прямой линии

Это новое число z наверняка не входит в наш список; действительно, оно не равно первому числу, стоящему в списке, так как от него отличается первой цифрой после запятой, оно не равно второму числу, так как от него отличается второй цифрой после запятой, и вообще отлично от n-го числа по списку, так как отличается от него n-й цифрой после запятой. Итак, в нашем списке, составленном будто бы из всех действительных чисел, нет числа z. Значит, множество всех действительных чисел несчетно.

Читателю может прийти в голову мысль, что несчетность континуума обусловливается неограниченной протяженностью прямой линии и что конечный отрезок прямой будет содержать лишь счетное множество точек. Чтобы убедиться в ложности такого предположения, достаточно установить, что весь числовой континуум в целом эквивалентен некоторому конечному интервалу, скажем, единичному интервалу от 0 до 1. Получить необходимое для этой цели взаимно однозначное соответствие можно, например, сгибая интервал в точках и и затем проектируя так, как показано на рис. 20. Отсюда видно, что даже конечный интервал (и, конечно, отрезок) содержит несчетное множество точек.

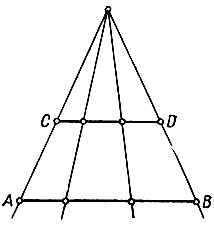
Упражнение. Показать, что любой отрезок [А, В] числовой прямой эквивалентен любому другому отрезку [С, D] (рис. 21).

Рис. 21. Взаимно однозначное соответствие между точками двух отрезков различной длины

Стоит привести еще другое доказательство несчетности континуума, носящее, пожалуй, более интуитивный характер. Достаточно (принимая во внимание последнее доказанное предложение) сосредоточить внимание на точках единичного отрезка от 0 до 1. Доказательство, впрочем, как и раньше, будет «косвенное». Предположим, что множество всех точек названного отрезка может быть расположено в виде последовательности

Источник

Доказать что множество рациональных чисел счетно

Случайно наткнулся на небольшую милую статью о красивом способе подсчёта рациональных чисел.

«Пересчитать» множество с помощью натуральных чисел проще всего, выстроив элементы данного множества в бесконечный ряд, и позаботившись при этом, чтобы каждый элемент в этом ряду на каком-то месте оказался. Например, пересчитать целые числа можно так:

Стандартный способ пересчёта рациональных чисел вот какой:

(ради простоты здесь и далее будем подсчитывать только положительные рациональные числа; если их можно «пересчитать» натуральными, то 0 и отрицательные к ним можно добавить при помощи того же трюка, который позволяет пересчитать целые числа)

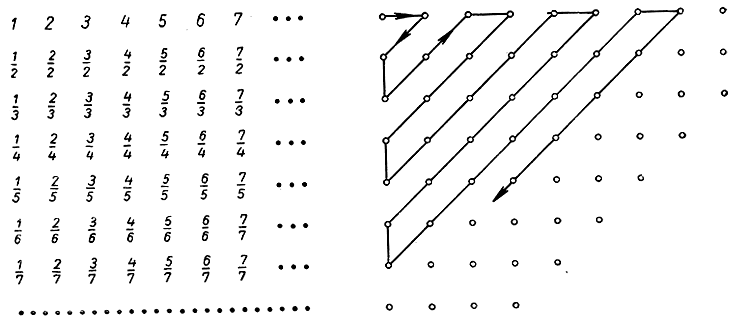
Сначала мы выстраиваем все положительные рациональные числа в бесконечном квадрате: строки и столбцы квадрата перенумерованы натуральными числами, а внутри квадрата в каждой клетке стоит рациональное число, равное частному номера столбца и номера строки. Ясно, что каждое рациональное число находится в этом квадрате. А затем мы его пересчитываем «по диагоналям» (картинка справа), начиная с левого верхнего угла, потом диагональ размером в два числа, потом следующая итд. итд. Ясно, что двигаясь таким образом, мы рано или поздно дойдём до любого числа в квадрате, а значит, в нашем списке будут все положительные рациональные числа.

Этот стандартный способ очень прост, но у него есть эстетические недостатки: например, в этом списке есть повторы: каждое рациональное число повторяется в нём бесконечное число раз (например, 1/2 встречается также как 2/4, 4/8 итд.) Это не мешает доказательству, т.к. эти повторы можно просто выбрасывать, строя список, но тогда для общего его члена не будет красивой лёгкой формулы.

Всё это не слишком важные вопросы, и, тем не менее, красивый другой способ пересчёта рациональных чисел, описанный в прочитанной мной статье, и свободный от этих недостатков, мне очень понравился. Ничего нового он не доказывает, он просто демонстрирует красивую конструкцию, а также, при доказательстве свойств этой конструкции, силу принципа наименьшего элемента, который гласит, что в любом непустом множестве натуральных чисел есть наименьший элемент.

Принцип наименьшего элемента эквивалентен принципу математической индукции по натуральным числам. Их можно легко доказать один с помощью другого. Например, предположим, что какое-то утверждение S выполняется для числа 1, и если оно выполняется для всех k 1, то S выполняется для всех k

Итак, вот эта конструкция. Построим бесконечное дерево, в вершинах которого находятся положительые рациональные числа, следующим образом:

Например, вот несколько первых членов последовательности f(k) (из картинки выше):

1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4

А f(10)=5, и для десятки есть пять способов: 8+2, 8+1+1, 4+4+2, 4+4+1+1, 4+2+2+1+1.

Наконец, докажем строго, что f(k) имеет именно этот смысл. Для этого построим рекурсивное определение f(k) и докажем, что b(k), если обозначить так кол-во способов представить k в виде суммы степеней двойки, не используя каждую более чем дважды, удовлетворяет тому же определению.

Источник

Счетность множества рациональных чисел

Теорема: множество рациональных чисел является счётным.

Необходимо доказать, что между множеством рациональных чисел и множеством натуральных чисел можно установить взаимо-однозначное соответствие. Для этого положительные рациональные числа запишем так:

Таким образом, будет записано каждое положительное число. Например, число 7/31 будет записано в 31-й строке в 7-м столбце. Вообще, дробь m/n будет записана в n-й строке m-м столбце.

Для установления взаимно-однозначного соответствия теперь уже нельзя переходить от столбца к столбцу, потому что в каждом столбце содержится бесконечное множество элементов. Для доказательства этой теоремы будем использовать диагональный метод Кантора. Он заключается в том, что мы подходим к каждому рациональному числу и, следовательно, каждому рациональному числу будет поставлено в соответствие какое-либо натуральное число.

Так, с помощью диагонального метода устанавливаем взаимно-однозначное соответствие между множеством положительных рациональных и множеством натуральных чисел, а это значит, что множество положительных рациональных чисел счетно.

Также можно доказать, что множество отрицательных рациональных чисел счётно. Сложив эти два множества и прибавив к ним конечное множество, состоящее из элемента нуль, мы получим всё множество рациональных чисел.

Теорема.Множество всех действительных чисел несчетно.

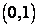
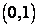
Доказательство. Для доказательства достаточно установить, что множество действительных чисел интервала образует несчетное множество. Допустим противное, что интервал есть счетное множество, т. е. все его точки можно перенумеровать:

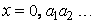
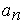
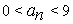
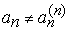
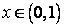
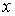
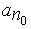
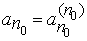
Но это предположение противоречиво. В самом деле, построим вещественное число , где цифры подобраны так, чтобы и . Ясно, что , однако не совпадает ни с одним из чисел , так как иначе должно было бы быть , что не имеет места.

Источник

Счетность множества рациональных чисел.

Дата добавления: 2015-08-14 ; просмотров: 3825 ; Нарушение авторских прав

Школьная математика имеет дело в основном с рациональными числами.

Рациональным числом называется число вида:

Что мы умеем делать с этими числами?

1) Складывать и вычитать:

Если 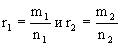, то

2) Умножать и делить:

Если

Но в связи с изучаемыми понятиями для нас нужна следующая теорема.

Теорема. Множество рациональных чисел счетно.

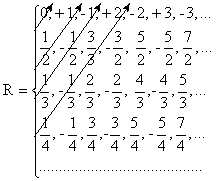
Представим множество всех рациональных чисел в виде бесконечной таблицы.

Оценим, как строятся строки этой таблицы.

Первая строка – это все целые числа, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.

Вторая строка – это все несократимые дроби со знаменателем 2, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.

Третья строка – это все несократимые дроби со знаменателем 3, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.

Вообще,n-ая строка это все несократимые дроби со знаменателем n, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.

Очевидно, что в этой таблице находятся все рациональные числа. Используя снова прием диагонализации представим R в виде:

Так как R представилось в форме последовательности, то отсюда следует, что R –счетное множество.

Не нашли то, что искали? Google вам в помощь!

Источник

Счетные множества

Множество называется счетным, если оно равномощно множеству 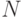натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

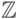
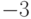
Например, множество целых чисел счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

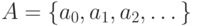
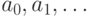
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

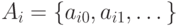
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник