Доказать что парабола и прямая не пересекаются
Как решать задачи на квадратичную функцию
В предыдущем уроке мы подробно разобрали, как построить параболу. В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Подставим в исходную функцию вместо « y » ноль и решим полученное квадратное уравнение.
0 = x 2 − 3
x 2 − 3 = 0
x1;2 =
| 0 ± √ 0 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| ± √ 12 |
| 2 |
x1;2 =
| ± √ 4 · 3 |
| 2 |
x1;2 =
| ± 2√ 3 |
| 2 |
x1;2 = ±√ 3
| x1 = √ 3 | x2 = − √ 3 |
Как найти при каких значениях « x » квадратичная функция принимает заданное числовое значение
Чтобы найти при каких значениях « x » квадратичная функция принимает заданное числовое значение, нужно:
При каких значениях « x » функция принимает значение « −3 ».
Подставим в исходную функцию вместо « y = −3 » и найдем « x ».
−3 = x 2 − x − 3
x 2 − x − 3 = −3
x 2 − x − 3 + 3 = 0
x 2 − x = 0
x1;2 =
| 1 ± √ 1 2 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
| 1 ± √ 1 |
| 2 |
x1;2 =
| 1 ± 1 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 1 | x2 = 0 |
Как найти координаты точек пересечения параболы и прямой
Чтобы найти точки пересечения параболы с прямой нужно:
Найти координаты точек пересечения параболы « y = x 2 » и прямой « y = 3 − 2x ».
Приравняем правые части функций и решим полученное уравнение относительно « x ».
x 2 = 3 − 2x
x 2 − 3 + 2x = 0
x 2 + 2x − 3 = 0
x1;2 =
| 2 ± √ 2 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| 2 ± √ 4 + 12 |
| 2 |
x1;2 =
| 2 ± √ 16 |
| 2 |
x1;2 =
| 2 ± 4 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 3 | x2 = −1 |
Теперь подставим в любую из заданных функций (например, в полученные числовые значения « x », чтобы найти координаты « y » точек пересечения.
1) x = 3
y = 3 − 2x
y(3) = 3 − 2 · 3 = 3 − 6 = −3
(·) A (3; −3) — первая точка пересечения.
2) x = −1
y = 3 − 2x
y(−1) = 3 − 2 · (−1) = 3 + 2 = 5
(·) B (−1; 5) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Как определить, принадлежит ли точка графику функции параболы
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.
Как найти точки пересечения параболы с осями координат
Найти координаты точек пересечения параболы с осями координат.
Сначала определим точки пересечения функции с осью « Ox ». На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата « y » точек пересечения с осью « Ox » равна нулю, поэтому подставим « y = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем их координаты по оси « Ox ».
0 = x 2 −3x + 2
x 2 −3x + 2 = 0
x1;2 =
| 3 ± √ 3 2 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
| 3 ± √ 9 − 8 |
| 2 |
x1;2 =
| 3 ± √ 1 |
| 2 |
x1;2 =
| 3 ± 1 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 2 | x2 = 1 |
Теперь найдем координаты точки пересечения с осью « Oy ».
Как видно на рисунке выше, координата « x » точки пересечения с осью « Oy » равна нулю.
Подставим « x = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем координату точки по оси « Oy ».
y(0) = 0 2 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Как определить при каких значениях x функция принимает положительные или отрицательные значения
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
С помощью графика квадратичной функции, изображенного на рисунке, ответить: При каких значениях « x » функция принимает 1) положительные значения; значения.
Проведем через точки, где график функции пересекает ось « Ox » прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает « x » в каждой из выделенных областей.
Ответ: при « x » и « x > 2 » функция принимает отрицательные значения; при функция принимает положительные значения.
Доказать что парабола и прямая не пересекаются
Глава 20. Парабола
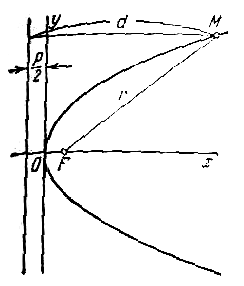
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
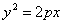
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
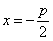
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле
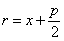
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
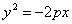
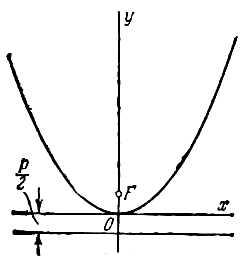
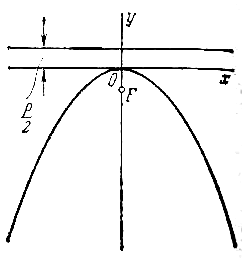
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
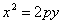
если она лежит в верхней полуплоскости (рис.), и
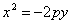
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
Доказать что парабола и прямая не пересекаются
В точке `(0,0)` кривые пересекаются под прямым углом, т.к. касаются осей координат.
И как доказать, что в точке `(0,0)` кривые пересекаются под прямым углом? Или написать как у вас в решении?
И можно узнать, где вы эту формулу взяли, я искал ее так и не мог найти.
`y’=-1/2` при `x=1` У меня получается 2 производные. Я чото понять не могу, как правильно то?
У меня график нарисован. Зачем мне проверять, что график `y=x^2` касается оси `Ox` в начале координат? Подставить точку `0` и будет `(0,0)`, это вся проверка?
Я вижу, что кривая `y^2=x` получается в результате поворота кривой `y=x^2`
Как обяснить то, что в точке `(0,0)` кривые пересекаются под углом `90^@`? Я понять не могу.
Я не могу понять чему равно `k_2` ведь там 2 производные получается. Я что-то понять не могу, объясните пожалуйста.
1) Все понял.
2)`y=x` прямая проходящая через начало координат, больше она нигде ось `Ox` не пересекает. Вы это хотели, чтобы я написал?
Я так и не понял как написать что в точке `(0,0)` кривые пересекаются под прямым углом. Или
это так очевидно, что можно просто написать и все?
Я просто ночью плохо соображаю, поэтому и прошу помощи. Я хочу разобраться. Я понимаю, что бред иногда пишу, но все-таки.
Доброй ночи. Afu-Ra, не думаю, что Вы еще здесь, но на всякий случай ( вдруг это чем-то поможет. )
Простите, я тут как-то «внаглую» влезаю в чужие записи. Если веду себя некорректно — кто-нибудь, скажите мне, и «я больше не буду»
1) Да конечно такого постороннего корня нет, я какой-то бред написал воще. Воще как так я такой бред написал, я сам незнаю.
`k_1=0` `=>` касательная к графику `y=x^2` это прямая `y=0` ось `Ox`
Спасибо большое за помощь, вы мне очень помогли.
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Доказать, что две параболы, имеющие общие ось и фокус, расположенный между их вершинами, пересекаются под прямым углом.
Доказать, что две параболы, имеющие общую ось и общий фокус, расположенный между их вершинами, пересекаются под прямым углом.
Уравнение прямой проходящей через точку и пересекающей ось Oz под прямым углом
Составить уравнение прямой проходящей через точку M(3,-1,1) и пересекающей ось Oz под прямым углом.
Доказать, что две кривые безразличия не пересекаются
Доказать,что 2 кривые безразличия не пересекаются 1)графическим способом 2)логическим способом.
Доказать,что в любом графе с n вершинами есть минимум две вершины с одинаковой степенью
Помогите пожалуйста доказать,что в любом графе с n вершинами есть минимум две вершины с одинаковой.
Групповое перемещение квадратов под прямым углом
Здравствуйте. Появился вопрос по макросу. Имеется макрос, который совершает ортогональный сдвиг.
Доказать, что из центра вписанного круга каждую сторону треугольника видно под тупым углом
Помогите решить задачу на доказательство, пожалуйста. Доказать, что из центра вписанного круга.
под прямым углом к фарватеру преодолеть реку шириной h метров
В универе задали на контрольной,помогите пожалуйста,срочно!! Java Задача: Человеку надо прямым.
Под каким углом пересекаются касательные к параболам
Доброго времени суток. При подготовке столкнулся с заданием: Под каким углом пересекаются.

На плоскости заданы 2 прямые у=a1x+b1 и у=а2x+b2 определить под каким углом они пересекаются.

Через точку K(1,2,1) провести плоскость пересекающую кривую x=t,y=t^2, z =-t под прямым углом