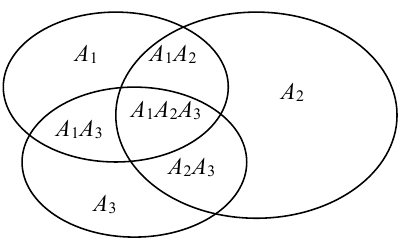
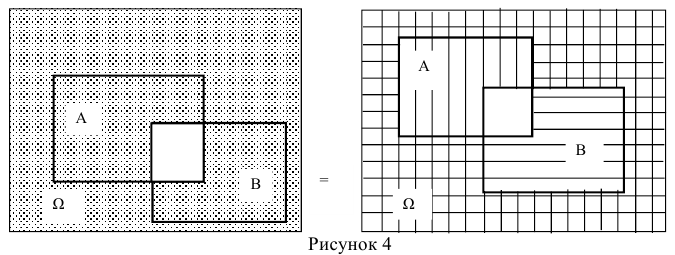
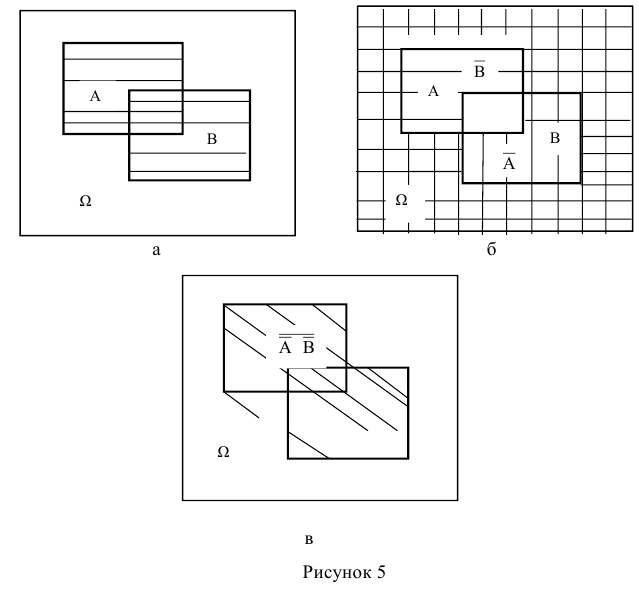
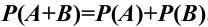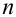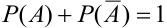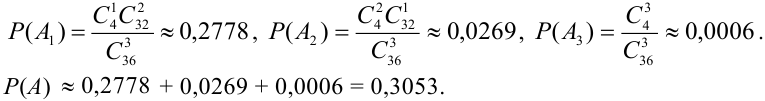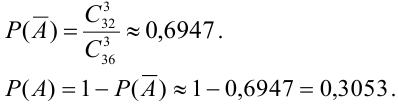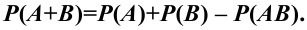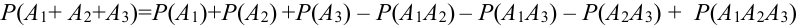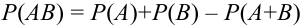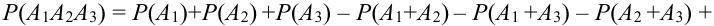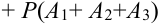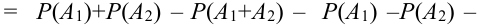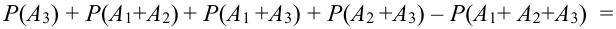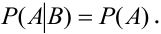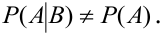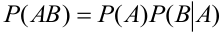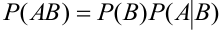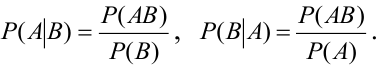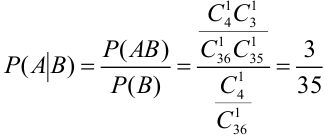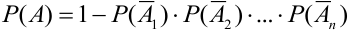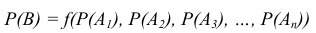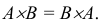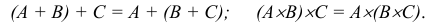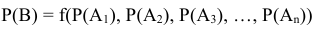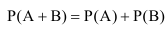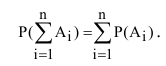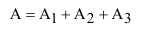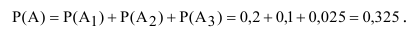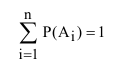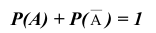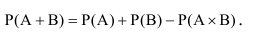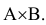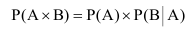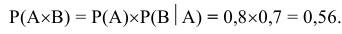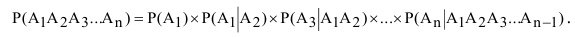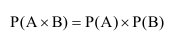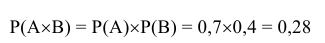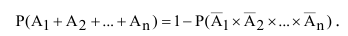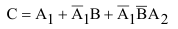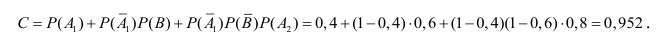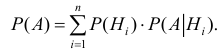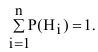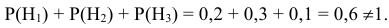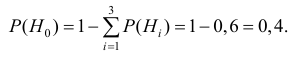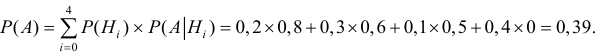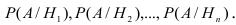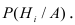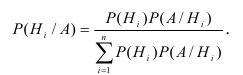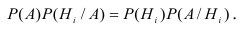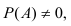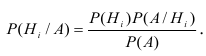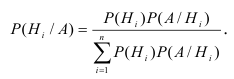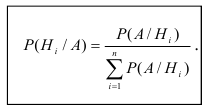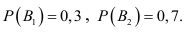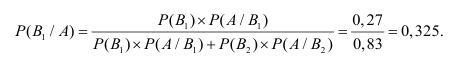Доказать что события образуют полную группу
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
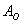
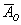
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
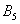
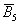
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
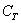
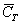
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 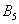
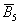
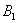
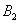
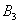
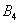
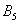
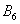
События 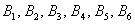
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 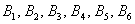
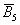
В примере с картами события 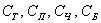
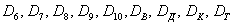
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
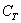
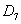
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
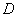
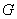
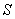
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Полная группа событий



Доказательство:
Противоположными событиями являются например, выпадение герба и выпадение цифры при бросании монеты; попадание и промах при стрельбе в цель; событие «день дождливый» и «день ясный»; события «3 дня подряд шел снег» и » хотя бы в один из 3-х дней снега не было».
Следствие: Сумма вероятностей противоположных событий равна 1.
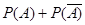
Переход к противоположному событию нередко облегчает вычисление вероятности. На практике весьма часто оказывается легче вычислить вероятность противоположного события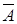
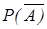
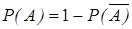
Вероятности противоположных событий принято обозначать p и q, следовательно p+q=1.
Содержание:
Основные теоремы теории вероятностей:
Теоремы сложения вероятностей
Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Доказательство.
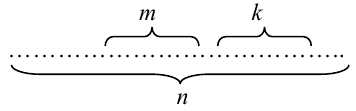
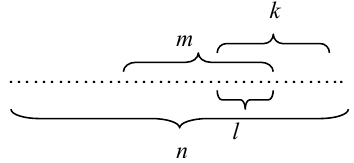
Докажем теорему для схемы случаев. Пусть всевозможные исходы опыта сводятся к совокупности случаев, которые можно наглядно изобразить в виде
Теорема 1 (Обобщенная теорема сложения несовместных событий) Вероятность суммы 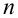
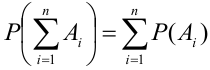
Доказательство (методом математической индукции).
Предположим, что теорема справедлива для 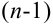
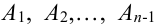
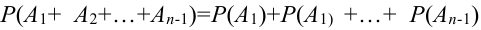
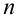
Обозначим 
Имеем 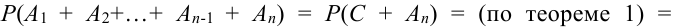
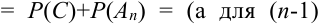
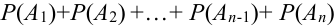
Следствие 1. Если события 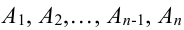
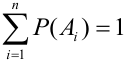
Доказательство.
Т.к. события несовместные, то к ним применима обобщенная теорема сложения:
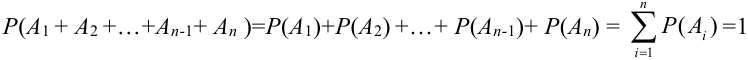
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Доказательство.
События А, 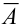
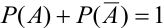
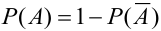
В формулировке таких задач встречаются слова «хотя бы», «не менее», «по крайней мере» и др.
Пример:
Из колоды карт (36) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение.
1 способ (по теореме 1′).
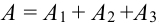
Т.к. события несовместны, то по теореме 1′: 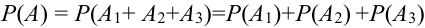
Найдем отдельно вероятности событий.
2 способ (по следствию 2).
Событие 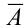
Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих
событий без вероятности их произведения (совместного осуществления):
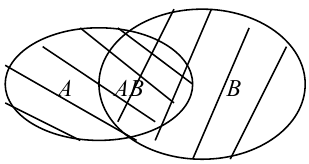
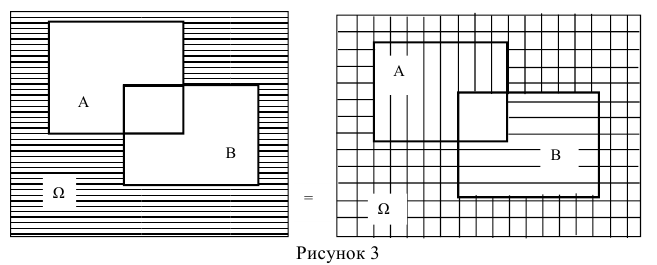
Доказательство (геометрическое)
События отождествляют с множествами. Два раза накладываем «лепесток» друг на друга, поэтому и отнимаем его. (что и треб. доказать)
Теорема 2 ( Обобщенная теорема сложения совместных событий).
Вероятность суммы 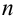
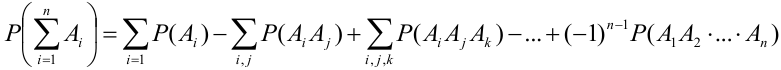
Для трех совместных событий теорема запишется в виде:
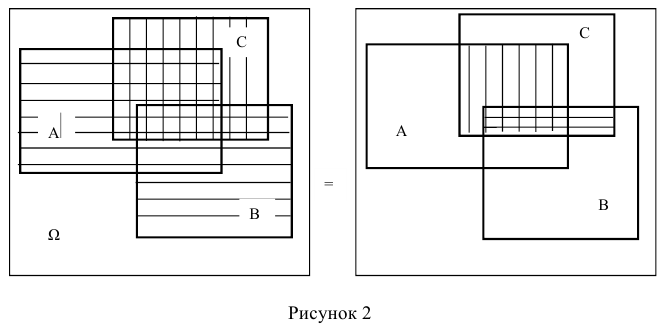
Доказательство для трех событий (геометрическое):
События отождествляют с множествами (см. рис.). (что и треб. доказать)
Замечание. Аналогичную формулу можно написать для произведения совместных событий:
Пример:
Для поражения самолета необходимо, чтобы были поражены оба двигателя (события 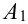
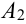
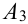
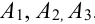
Решение.
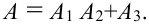
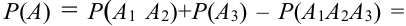
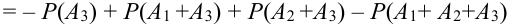
Теоремы умножения вероятностей
Определение 21. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Определение 22. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Примеры:
3) В урне 2 белых и 1 черный шар. Двое Таня и Ваня вынимают из урны по одному шару. Зависимы или независимы события: А = <появление белого шара у Тани>, В = <появление белого шара у Вани>?
Решение.
Найдем вероятности событий. 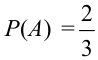
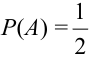
Определение 23. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Определение 24. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.
Определение 25. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 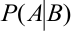
В Примере 3): 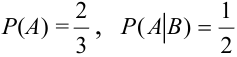
Условие независимости события А от события В:
Условие зависимости события А от события В:
Теорема 3. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
Доказательство.
Докажем для схемы урн истинность тождества формулы.
Пусть всевозможные исходы опыта сводятся к 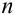
Тогда, вероятности данных событий равны: 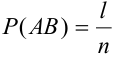
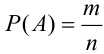
Вычислим условную вероятность 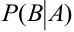
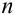
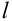
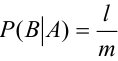
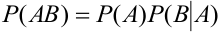
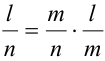
Замечание 1. При применении теоремы вполне безразлично, какое из событий А или В считать первым, а какое вторым, т.е. теорему можно записать в виде:
Замечание 2. В общем случае при 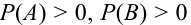
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Замечание 3. Зависимость и независимость событий всегда взаимны.
Замечание 4. Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:
1. 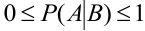
2. если наступление события В исключает возможность осуществления А, т.е. 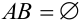
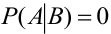
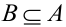
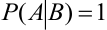
3. Если 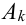
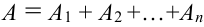
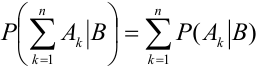
4. 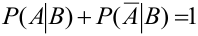
Замечание 5. Если А и В независимы, то независимы также события 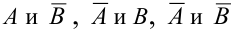
Теорема 3. ( Обобщенная теорема умножения зависимых событий).
Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что всс предыдущие имели место:
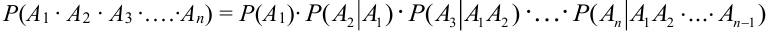
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 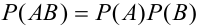
Теорема 4. ( Обобщенная теорема умножения независимых событий).
Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:
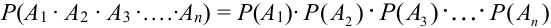
Пример:
Из колоды карт последовательно вынуты две карты. Найти: а) вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), б) вероятность того, что вторая карта будет тузом, если первоначально тоже был вынут туз.
Решение.
Или можно было найти эту вероятность, используя формулу условной вероятности:
Пример:
В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что а) оба белые, б) оба белые, если после первого вынимания шар возвращают обратно в урну, и шары перемешиваются.
Решение.
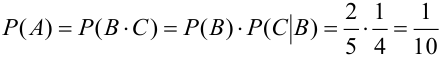
Теорема 5. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 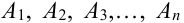
Если все 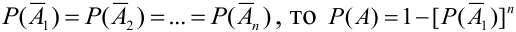
Пример:
Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно 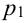
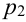
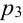
Решение.
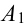
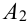
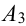
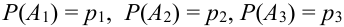
Перейдем от прямого события к противоположному: 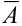
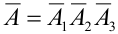
где 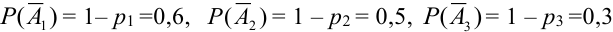
Тогда по теореме 5:
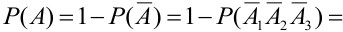
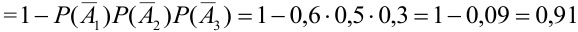
Основные формулы для вычисления вероятностей
Ограниченность классического и статистического способов определения вероятности событий, приемлемых, главным образом, для определения вероятности простых событий, приводит к тому, что в подавляющем большинстве случаев ни один из этих способов в чистом виде для решения задачи определения наступления событий применить не удаётся.
Факт сложности или невозможности определения вероятности сложных событий явился стимулом разработки аппарата теории вероятностей, с помощью которого вероятность определяется не прямым, а косвенным методом через вероятность более простых событий.
Сущность косвенного метода определения вероятности сложного события заключается в следующем: вначале анализируют условия испытания и устанавливают события 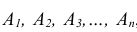
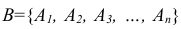
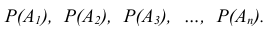
Однако определению вероятности наступления сложного события как комбинации более простых событий должны предшествовать твёрдые знания правил применения рассмотренных в лекции теорем сложения (объединения) и умножения (пересечения) событий.
Этому вопросу и будет посвящён вопрос нашего занятия.
Пример:
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя операции сложения (объединения) и умножения (пересечения) событий представим сложное событие D= < поражение артиллерийской батареи>как комбинацию простых событий. Результат проиллюстрируем диаграммой Эйлера-Венна.
Обозначим через событие А = <поражение первого взвода орудий>, через событие В = <поражение второго взвода орудий>, С = <поражение центра управления огнём>. Тогда событие D = <поражение артиллерийской батареи>определится как поражение либо центра управления огнём (событие С) либо одновременно первого взвода орудий (событие А) и второго взвода орудий (событие В), т.е. будет иметь место следующая комбинация событий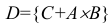
Для решения такого типа задач необходимо усвоить ряд основных свойств, которыми обладают действия над событиями.
Операции сложения (объединения) и умножения (пересечения) событий обладают рядом свойств, аналогичным свойствам сложения и умножения чисел.
1. Переместительное свойство:
А + В = В + А;
2. Сочетательное свойство:
3. Распределительное свойство:
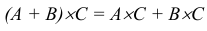
4. Операции прибавления пустого множества и умножения на пустое множество аналогичны операциям над числами, если считать пустое множество за ноль.
Ряд операций над событиями уже не обладают свойствами по аналогии с арифметическими действиями, например:
5. 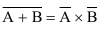
6. 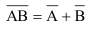
7. 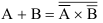
Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности
На предыдущей лекции мы говорили о том, что достаточно часто определить вероятность сложного события трудно или вообще невозможно. Для чего научились представлять события, как комбинацию других более простых событий используя понятия суммы (объединения) или произведения (пересечения) событий.
Вспомним пример, рассматриваемый нами на предыдущей лекции:
На сегодняшнем занятии мы ответим на следующий вопрос: как определить вероятность сложного события представляющего собой функцию известных или заданных вероятностей
При определении вероятностей сложных событий пользуются теоремами сложения и умножения вероятностей. Эти теоремы теоретически могут быть доказаны только для таких событий, вероятность появления которых может быть определена классическим способом. Для других событий эти теоремы принимаются как аксиомы. Поэтому мы не будем показывать доказательство этих теорем, а ограничимся только понятием «правила», понимая при этом ряд теорем и следствий из них, с помощью которых определяется вероятность комбинации событий.
Правила сложения вероятностей
Аксиома: Вероятность суммы или наступления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий (аддитивность Р):
Данную аксиому иногда называют «теоремой сложения», так как для опытов, сводящихся к «схеме случаев», она может быть доказана.
Эта аксиома легко обращается на любое число несовместных событий: вероятность суммы несовместных событий равна сумме вероятностей этих событий:
Пример №1
Решение:
Обозначим интересующее нас событие через А = <попадание в танк>, тогда 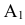
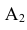
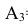
А так как события 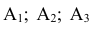
Вывод: полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 325 случаях из 1000 будет получено попадание в танк.
Из данной аксиомы вытекают два важных следствия.
Следствие 1. Если события 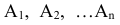
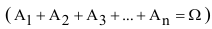
Следствие 2. Сумма вероятностей противоположных событий равна 1.
Для совместных событий аксиома примет следующий вид:
Вероятность суммы, или наступление хотя бы одного из двух совместных событий, равна сумме вероятности этих событий без вероятности произведения этих событий:
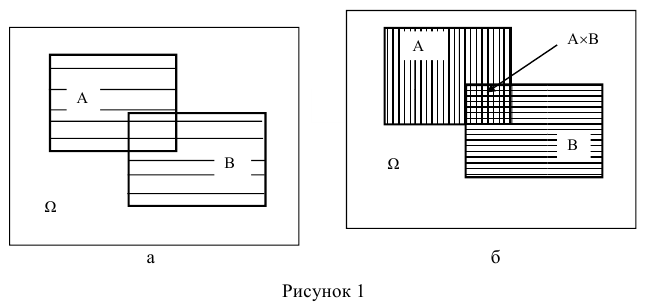
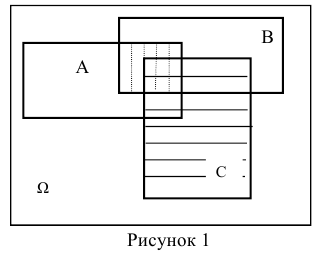
Справедливость этого тождества наглядно следует из его геометрической интерпретации (рисунок 1).
На диаграмме Эйлера-Венна вероятность наступления событий А (или
Пример №2
Решение: Пусть событие А = <подавление личного состава батареи>, а событие В= <повреждения материальной части>. Тогда одновременное подавление личного состава и повреждение материальной части будут являться совместным наступлением событий А и В или
Вероятность наступления события А по условию задачи равна 0,15 (Р(А)=0,15), вероятность наступления события В равна 0,45 (Р(В)=0,45), вероятность совместного наступления события А и В равна 0,25 (Р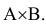
Требуется найти вероятность события С =<подавления батареи противника>, которое будет заключаться либо в подавлении личного состава батареи, либо в повреждении материальной части либо того и другого, или Р(А+В).
Применив теорему сложения вероятностей, получим:
Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 35 случаях из 100 батарея противника будет подавлена, т.е. поражён либо личный состав, либо повреждена техника, либо и то и другое.
Правила умножения вероятностей
Перед рассмотрением правил умножения вероятностей введём ряд новых понятий, которые необходимы для логического понимания производимых над событиями действий.
Событие А называется независимым от события В, если вероятность наступления события А не зависит от того, произошло ли событие В.
Событие А называется зависимым от события В, если вероятность наступления события А меняется в зависимости от того, произошло событие В или нет.
В качестве примеров зависимых событий можно привести следующие:
Пример №3
Раз нам требуется определить вероятность совместного наступления двух зависимых событий, одно из которых может наступить только при том условии, что имело место другое из них, введём понятие условной вероятности события.
Вероятность события В, вычисленная при условии, что имело место другое событие А называется условной вероятностью события В по отношению к событию А (обозначается 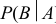
Теорема: Вероятность произведения или совместного наступления двух любых случайных событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
Пример №4
Вероятность попадания в танк при одном выстреле равна 0,8; вероятность поражения экипажа танка при попадании в танк равна 0,7. Определить вероятность поражения экипажа танка при одном выстреле.
Решение:
Пусть событие А = <попадание в танк при одном выстреле>, а событие В = <поражение экипажа танка>. Интересующее нас событие С = <поражение экипажа танка при одном выстреле>будет иметь место только в том случае, если наступит событие А, при этом наступление события С возможно только тогда, когда одновременно наступят события А и В.
Вероятность наступления события А по условию задачи равна 0,8 (Р(А)=0,8); вероятность наступления события В равна 0,7 (Р(В)=0,7).
Требуется найти вероятность поражения экипажа танка при одном выстреле, которая будет являться произведением вероятностей попадания в танк при одном выстреле и поражении экипажа танка при условии что имело место попадание в него, т.е. Р(С)=Р(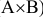
Применив теорему умножения вероятностей, получим:
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях по одному выстрелу в каждом в среднем в 56 случаях из 100 экипаж танка будет поражён.
Правило умножения вероятностей легко обращается на случай произвольного числа событий:
Из данной теоремы вытекает ряд важных следствий.
Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Пример №5
Решение:
Вероятность наступления события А по условию задачи равна 0,7 (Р(А)=0,7), вероятность наступления события В равна 0,4 (Р(В)=0,4).
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 28 случаях из 100 в цель попадут оба студента.
Зависимость и независимость событий всегда взаимны. Если событие А не зависит от события В, то и событие В не зависит от события А. Таким образом, можно уточнить данное ранее определение независимых событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Из рассмотренных выше правил сложения и умножения вероятностей вытекает ещё одно очень важное следствие: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию:
Пример №6
Решение:
Обозначим за событие 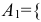
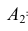
Так как события 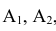
Вывод: полученный результат означает, что при проведении достаточно большого числа испытаний в аналогичных условиях в среднем в 95 случаях из 100, танк будет поражён.
Формула полной вероятности
При изложении третьего вопроса лекции преподаватель на примере поражения движущегося танка обозначает проблему определения вероятности сложного события (давая при этом понятие гипотезы).
После чего преподаватель доводит условие задачи (Пример 7), формулу для вычисления полной вероятности события (без её вывода) и условия её применения.
При постановке задачи и пояснения физической сущности вопроса преподаватель использует оверхэд-проектор и подготовленные слайды.
Решение задачи преподаватель проводит на доске, особое внимание при этом обращая на методику её решения и порядок записи. В заключении решения задачи преподаватель под запись доводит вывод, отражающий физическую сущность полученного результата.
При решении ряда практических задач вычисление вероятности некоторого сложного события можно существенно облегчить, если связать наступление этого события с наступлением единственно возможных и несовместных событий, под которыми понимаются гипотезы о всех возможных исходах испытаний.
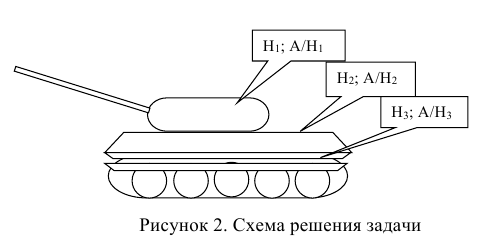
Пусть, например, производится выстрел по танку (рисунок 2).
Под гипотезами понимают полную группу единственно возможных несовместных событий, которые могут наступить в результате проведения испытаний.
В условиях нашей задачи гипотезы о возможном исходе стрельбы будут следующие:
Вероятности этих гипотез 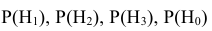
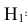
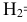
Указанные условные вероятности возможно определить опытным путём, проводя полигонные стрельбы по танку.
Пример №7
Известны также вероятности попадания снаряда в каждый из отсеков танка. Вероятность попадания в башню танка равна 0,2. Вероятность попадания в корпус равна 0,3; вероятность попадания в ходовую часть равна 0,1.
Требуется определить вероятность поражения танка при одном выстреле.
Вычислить вероятность наступления интересующего нас события позволяет формула, получившая особое название формулы полной вероятности.
Полная вероятность события равна сумме парных произведений вероятностей каждой из гипотез на отвечающие им условные вероятности наступления этого события.
При определении полной вероятности необходимо следить, чтобы были учтены все гипотезы о возможном исходе испытания, при которых может наступить интересующее нас событие, т.е. гипотезы должны составлять полную группу несовместных событий. Свидетельством полного учёта всех гипотез является выполнение равенства
Если данное равенство не выполняется, то это означает, что учтены не все гипотезы о возможных исходах испытания.
Вернёмся к решению примера.
Решение:
Таким образом, возможные гипотезы об исходах стрельбы:
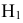
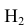
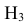
По условию задачи вероятности гипотез будут равны:
гипотеза 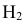
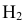
Интересующее нас событие А = <поражение танка>. По условию задачи вероятность поражения танка при реализации гипотез:
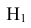
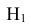
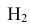
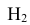
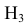
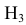
Проверим, все ли гипотезы об исходах стрельбы учтены:
Таким образом, вероятность гипотезы 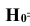
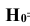
Вероятность поражения танка при реализации гипотезы 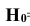
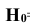
Применяя формулу полной вероятности для решения задачи получим:
Следовательно, полная вероятность поражения танка при одном выстреле равна
Вывод: Полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 39 случаях из 100 танк окажется поражённым.
Формула Байеса, вероятность появления хотя бы одного события
Пусть имеется полная группа несовместных гипотез 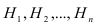
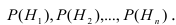
Требуется определить какие вероятности имеют гипотезы 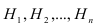
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.
Эта формула называется формулой Байеса.
Доказательство.
По Теореме умножения вероятностей получаем:
Тогда если
Для нахождения вероятности Р(А) используем формулу полной вероятности.
Если до испытания все гипотезы равновероятны с вероятностью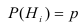
Пример №8
Решение: пусть событие 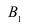
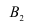
Пусть событие А означает появление надёжного прибора. По условию примера вероятность события А при условии, что появится прибор, собранный специалистом высшей квалификации, 
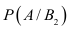
Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события 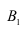
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.