Докажите что не существует наибольшего четного числа

Закономерности в распределении простых чисел

Введение

Простое число — это натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Такие числа представляют огромный интерес. Дело в том, что никто так и не смог полностью понять и описать закономерность по которой простые числа располагаются в ряду натуральных чисел.

Ещё до нашей эры Евклид сформулировал и доказал первые теоремы о простых числах. С тех пор математики, среди них Гаусс, Ферма, Риман, Эйлер, продолжали исследования и надо отдать им должное заметно продвинулись. Было обнаружено много интересных свойств простых чисел, выдвинуто много предположений, некоторые из которых были доказаны. Однако много гипотез связанных с простыми числами до сих пор остаются необоснованными.

Распределение простых чисел

Первостепенная задача, решение которой автоматически привело бы к решению большинства вопросов связанных с простыми числами заключается в следующем:

Получить рекуррентную формулу для очередного простого числа

Существует родственная ей задача о количестве простых чисел, не превосходящих заданной величины:

Найти функцию p(x), значение которой в точке x равно числу простых чисел на отрезке [1, x]. Где x – любое действительное число не меньшее единицы.

Функция называется функцией распределения простых чисел.

К решению вышеуказанных задач существует множество подходов. Рассмотрим некоторые из них.

Основная теорема арифметики гласит, что любое натуральное число большее единицы может быть представлено в виде произведения простых множителей (причём единственным образом, с точностью до порядка множителей).

Отсюда и из определения простого числа следует, что натуральное число, большее двух, является простым тогда и только тогда, когда оно не делится ни на одно из простых чисел меньших самого себя.

Первое простое число p₁ =2. Значит все последующие простые числа должны не делится на 2, то есть иметь вид 2k+1, где k – натуральное. То есть все простые числа начиная со второго — нечётные.

Второе простое число p₂ = 3. Значит все последующие простые числа должны иметь вид 3m+1, либо 3m+2, где m – целое. Это равносильно утверждению о том, что все простые числа начиная с третьего не делятся на три. Однако при этом числа ещё должны не делится на два, то есть иметь вид 2k+1.

Решая диофантовы уравнения

найдём k и m и получим, что все простые числа начиная с p₃ обязательно представимы в виде , либо в виде , где t – целое.

И правда, какое бы простое число мы ни взяли оно представимо таким образом:

Однако обратное неверно, то есть любое натуральное число вида 6t+1 или 6t+5 не обязательно простое. Например, .

Третье простое число p₃ = 5. И если по аналогии учесть, что любое простое число, начиная с четвёртого не делится на 5, также не делится на p₁ = 2 и на p₂ = 3, то получим, что все простые числа начиная с p₄ обязательно имеют одно из представлений

Затем учтём p₄, p₅ и т.д. Проблема в том, что на каждом шаге нам придётся решать всё большую систему диофантовых уравнений, поэтому такой прямолинейный подход оказывается весьма сложным.

На самом деле, при различных попытках решения поставленной нами задачи в большом количестве случаев появляются одни и те же конструкции. Например, произведение Эйлера. Рассмотрим, как это происходит, на следующем примере.

Итак, как же найти функцию F(x)? Сначала рассмотрим множество всех натуральных чисел. Какова доля чисел, которые не делятся ни на одно из простых p₁, p₂, …, p_n?

Каждое второе число делится на p₁ = 2. Значит, часть всех чисел делится на p₁.

Каждое третье число делится на 3. Значит, всех чисел делится на p₂. При этом надо учесть, что каждое шестое число делится и на 2 и на 3 одновременно.

Значит, доля чисел не делящихся ни на 2, ни на 3 равна

Если преобразовать выражение, то оно примет вид:

Опять же можно представить выражение в виде

Будем обозначать такое произведение P(n). Кстати, если учесть все простые числа (n→∞), то мы получим обратную величину от так называемого произведения Эйлера.

Почему так происходит? Когда мы получали формулу (1), мы пользовались рассуждениями, что среди всех натуральных чисел доля, делящихся на p_n, равна . Но нельзя сделать такое утверждение о конечном наборе последовательных натуральных чисел. Например, возьмём набор 1,2, 3,4,5,6,7,8,9. Здесь 4 числа из 9 делятся на два. И несложно заметить, что отличается от . То есть, при применении к конечному набору чисел, данный метод даёт результат с некоторой погрешностью.

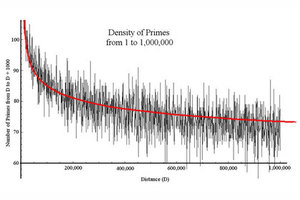
Это будет мешать далее получать точные формулы. Но если оценить эту погрешность, то можно (например, приняв и используя приведённые выше рассуждения) получить оценку для p_n+1-го простого числа. Однако, получение таких оценок — это тема отдельной работы. И поэтому здесь я не буду на этом останавливаться, а приведу лишь некоторые результаты, полученные математиками.

Одна из оценок для простого числа с номером n:

оценка верна для всех n, начиная с 6.

А вот формула для функции распределения простых чисел:

Для функции Риман получил приближение, используя интегральный логарифм и нетривиальные нули дзета-функции Римана. Однако, это приближение верно, только если верна гипотеза Римана. Причём если гипотеза Римана верна, то оно является наилучшим.

Гипотеза Римана до сих пор не доказана и не опровергнута. Она, как мы могли видеть, тесно связана с простыми числами и, вообще, имеет огромное значение для теории чисел. Из-за своей важной роли в математике, гипотеза Римана была объявлена одной из семи задач тысячелетия.

Проблемы Ландау

Насчёт простых чисел выдвинуто очень много интересных гипотез. Среди них видное место занимают гипотезы Ландау (проблемы Ландау). Формулируются они так:

1. Гипотеза Гольдбаха

Можно ли любое целое чётное число, большее 2, записать в виде суммы двух простых?

2. Гипотеза о числах-близнецах

Бесконечно ли число простых p таких, что p + 2 тоже простое?

3. Гипотеза Лежандра

Всегда ли существует по меньшей мере одно простое число, лежащее между двумя последовательными полными квадратами?

4. Гипотеза о почти квадратных простых числах

Существует ли бесконечно много простых чисел p вида .

Проблемы Ландау ни доказаны, ни опровергнуты по состоянию на 2020 год. Далее кратко расскажу про каждую из них.

1. Гипотеза Гольдбаха

Существуют две гипотезы Гольдбаха: слабая (тернарная) и сильная (бинарная).

Слабая гипотеза Гольдбаха: Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.

Эту гипотезу доказал Харольд Гельфготт в 2013 году используя так называемые большие дуги. Финальная часть доказательства заняла 133 страницы.

Сильная гипотеза Гольдбаха: Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.

Надо заметить, что в обоих случаях гипотезы Гольдбаха простые числа не обязательно должны быть различными.

Заметьте, что в сильной гипотезе речь идёт только о чётных числах. Давайте покажем, что нечётное число не обязано быть представимо в виде суммы двух простых чисел. Просто приведём пример. Число 11 не представимо в виде суммы двух простых. Вроде бы несложно.

Но переформулируем проблему так: существует ли такое число, что любое нечётное, большее этого числа, представимо в виде суммы двух простых чисел? Давайте проверим. Пусть существует некоторое нечётное натуральное число N, такое, что любое нечётное число представимо в виде суммы двух простых чисел.

Возьмём произвольное нечётное . По предположению существуют такие простые p₁ и p₂, что . Если сумма двух натуральных чисел нечётна, то это значит, что одно из слагаемых чётно, а другое нет. Пусть для определённости p₁ – чётное. Единственное чётное простое число — это 2. Значит, . То есть, K-2 (предыдущее перед K нечётное число) является простым. Поскольку всё вышесказанное верно для любого нечётного большего N, то получается, что все нечётные числа, начиная с N-2, являются простыми. Это неверно. Если бы это было так, то при n→ ∞. Однако, как говорилось выше при n→ ∞.

Итак, не существует такого числа, начиная с которого все нечётные числа могут быть представлены в виде суммы двух простых.

А что же насчёт чётных? Гипотеза не была опровергнута, не было найдено ни одного контрпримера. Но это не значит, что их не существует. Доказать же гипотезу полностью пока никому не удалось.

2. Гипотеза о числах-близнецах

Бесконечно ли число простых чисел близнецов?

Для начала сформулируем определение. Два простых числа называются близнецами если отличаются друг от друга на 2.

Так же доказано, что существует бесконечно много простых чисел, разница между которыми составляет 246. Это наилучшая из обоснованных на данный момент оценок. Если же использовать некоторые недоказанные гипотезы о простых числах, то оценку можно улучшить.

3. Гипотеза Лежандра

Всегда ли существует, по меньшей мере, одно простое число, лежащее между двумя последовательными полными квадратами?

Аналогичная гипотеза доказана для кубов, начиная с некоторого n. То есть, существует, по меньшей мере, одно простое число, лежащее между и для достаточно большого n. Для квадратов же, гипотеза Лежандра пока не доказана.

4. Почти квадратные простые числа

Заключение

Как мы видим, в этой области теории чисел существует очень много пробелов, а также недоказанных гипотез. Отдельно хочется сказать про численную проверку утверждений. Например, ни для одной из гипотез Ландау не был найден контрпример, даже с использованием значительных вычислительных мощностей в течение большого времени. Однако, в истории математики 20-го и 21-го века были случаи, когда контрпример, опровергающий гипотезу, был настолько огромным числом, что его не удавалось найти с помощью вычислительных машин.

Также, постоянный интерес к простым числам обусловлен их обширным применением в криптографии. Итак, как мы убедились, исследование простых чисел — это, действительно, важная и очень интересная задача.

Источник

Бог любит троицу Решена одна из старейших и сложнейших математических задач

Схематическое разбиение нескольких первых четных чисел в сумму простых

В середине мая 2013 года математик из Перу, в настоящее время работающий во Франции, Харальд Хельфготт выложил в архив препринтов Корнельского университета статью «Большие дуги для теоремы Гольдбаха». Эта статья объемом 133 страницы содержит финальную часть доказательства (начатого на заре XX века великим советским математиком Иваном Виноградовым) так называемой тернарной проблемы Гольдбаха — одной из старейших задач в теории чисел.

Май 2013 года стал совершенно удивительным месяцем для теории чисел (точнее, аналитической теории чисел, но это уже детали для специалистов): буквально за одну неделю стало известно о прогрессе в двух сложнейших проблемах, относящихся к так называемым аддитивным задачам. Если грубо, то это целый класс задач, которые имеют дело с представлением одних чисел в виде суммы других, причем эти другие берутся из какого-нибудь специального класса. Соответственно, большинство задач сводится к тому, существуют ли указанные представления и если да, то сколько их. Ответ на последний вопрос, конечно, дается не точный, а в виде какой-нибудь примерной оценки. К задачам этого класса относятся, например, задача Лежандра о представлении целого числа в виде суммы четырех квадратов натуральных чисел, задача о представлении натурального числа в виде суммы пяти квадратов простых чисел (простыми, напомним, называются числа, которые делятся только на себя и на единицу).

К аддитивным задачам относится общая проблема Варинга. В 1770 году Эдвард Варинг опубликовал работу, в которой высказал гипотезу: всякое натуральное число является суммой четырех квадратов, девяти кубов, девятнадцати четвертых степеней. В более общем и современном виде эта задача формулировалась так: доказать, что для любого k существует число g(k), зависящее только от k, такое, что всякое натуральное число является суммой g неотрицательных k-ых степеней. Эта задача, кстати, была решена Давидом Гильбертом еще в 1909 году.

Другой же задачей, которую, в отличие от чисел-близнецов, удалось решить полностью, стала так называемая тернарная задача Гольдбаха.

Записки на полях

В 1725 году немецкий математик и юрист Кристиан Гольдбах переехал в Россию, чтобы стать постоянным членом только что открывшейся Петербургской академии наук. Дела у математика достаточно быстро пошли в гору, и его приблизили ко двору — спустя всего несколько лет он был личным репетитором юного Петра II. В 1742 году уже немолодой Гольдбах (ему было 52 года) решает закончить карьеру ученого и принимает позицию чиновника в Коллегии иностранных дел. 7 июня этого же, судьбоносного для Гольдбаха года математик пишет письмо Леонарду Эйлеру, на тот момент проживавшему в Пруссии. С Эйлером Гольдбах познакомился еще до приезда в Россию во время своего образовательного турне по Европе после окончания университета и с тех пор поддерживал дружеские отношения.

В конце письма, уже на полях, Гольдбах пишет следующую гипотезу: «Всякое целое число больше двух можно представить как сумму трех простых» (немецкий математик, в отличие от представлений современной теории чисел, считал единицу также простым числом). В ответном письме Эйлер напоминает Гольдбаху, что ранее в личной беседе тот высказывал похожую гипотезу: мол, любое четное целое число можно представить в виде суммы двух простых. При этом Эйлер был уверен, что «это несомненно верная теорема», но говорил, что он ее «доказать не в состоянии». Так на свет появилась гипотеза Гольдбаха, точнее даже две гипотезы сразу.

Первая получила название тернарной (или слабой) гипотезы Гольдбаха. Она утверждает, что всякое нечетное целое число больше пяти представляется в виде суммы трех (не обязательно попарно различных) простых чисел. В свою очередь бинарная (или сильная) гипотеза Гольдбаха утверждает, что всякое целое четное число больше двух представляется в виде суммы двух (не обязательно различных) простых чисел. Эту гипотезу называют сильной потому, что слабая из нее вытекает: добавляя ко всем четным числам тройку, мы можем получить все возможные нечетные числа больше пяти.

Дуги большие и малые

К началу XX века гипотезы Гольдбаха, наряду с гипотезой Римана, стали одними из центральных задач теории чисел, войдя даже в состав знаменитой 8-й проблемы Гильберта.

Прорыв в решении этой задачи был совершен британскими математиками Гарольдом Харди и Джоном Литтлвудом. Тогда они изучали задачу Варинга (о ней говорилось выше). Развивая идеи самого Харди и Сириваса Рамануджана, заложенные в работах 1916-1917 годов, британские математики создали так называемый круговой метод. Его суть заключается в следующем: решение задачи (например, количество способов представить целое число в виде суммы трех простых) задается интегралом по единичной окружности от некоторого ряда. Этот интеграл разбивается на два, один из которых оценивается, а про другой доказывается его относительная малость. Составляющие первую сумму называются большими дугами, а вторую — малыми.

Если читатель споткнулся на этом месте, то вот как этот метод в беседе с «Лентой.ру» объяснил сам Харальд Хельфготт: «Анализ количества решений производится, по сути, посредством преобразования Фурье. Представьте себе, что простые числа — это звуки на некоторой записи, скажем, в моменты времени 2, 3, 5, 7, 11 и так далее микросекунд. После преобразования у вас получается своего рода шум, в котором вы пытаетесь услышать какие-то ноты. Среди них есть такие, которые слышны достаточно хорошо, — это и есть большие дуги. А есть частоты, которые просто являются шумовыми фрагментами, — это малые дуги. Весь метод распадается на две части — выделение нот и доказательство того, что остальное на самом деле шум. За первую часть метода отвечают оценки на большие дуги, за второй — на малые».

Используя свой метод, Харди и Литтлвуд сумели доказать тернарную гипотезу Гольдбаха. Однако у их доказательства был один, но крайне существенный изъян, который, по сути, перечеркивал всю работу: в статье они опирались на недоказанную обобщенную гипотезу Римана. Если коротко, то это некоторое утверждение о решениях одного уравнения — в гипотезе говорится, что все эти решения лежат на одной прямой на плоскости. Это утверждение настолько сложное, что оно не доказано до сих пор, и ее упрощенный вариант (известный просто как гипотеза Римана) входит в список задач Тысячелетия института Клея, за решение каждой из которых полагается по миллиону долларов. Гильберт даже шутил, что если бы он уснул и проснулся через 500 лет, то первым делом спросил бы, доказана ли гипотеза Римана.

Рукопись Кристиана Гольдбаха

Метод Харди и Литтлвуда был усовершенствован советским математиком Иваном Виноградовым. Благодаря этому в 1937 году Виноградов без использования гипотезы Римана доказал вот такой факт: все нечетные целые числа, начиная с некоторого N, можно представить в виде суммы трех простых. «Пожалуй, основным достижением Виноградова были оценки на малые дуги. На самом деле в круговом методе это сложная часть, и оценки Виноградова на тот момент были просто потрясающие — они были результатом крайне нетривиальных комбинаторных рассуждений. Для оценки же больших дуг он использовал методологию, очень похожую на ту, которая была у Харди и Литтлвуда», — рассказал Хельфготт.

Доказано — не доказано

С тех пор многие математики пытались улучшить результат Виноградова. Идея в основе всех этих попыток была довольно простой: улучшая оценки, добиться того, чтобы N стало достаточно малым. «Достаточно малым» в данном случае подразумевает такое значение, для которого гипотезу Гольдбаха можно проверить на компьютере.

«Я начал серьезно заниматься проблемой Гольдбаха в 2006 году, — рассказал «Ленте.ру» Хельфготт. — Достаточно быстро я понял, что могу улучшить существовавшие на тот момент оценки малых дуг. Результатом этой работы стали так называемые свободные от логарифмов оценки (эти результаты я получил достаточно быстро). Дальше работа двигалась намного медленнее — ведь я старался улучшать оценки не только количественно, но и качественно. С самого начала мне казалось, что без качественных улучшений в этой задаче не продвинуться».

В 2012 году свет увидела работа известного специалиста по теории чисел и филдсовского медалиста 2006 года Терренса Тао. Ему удалось показать, что всякое нечетное число представимо как сумма не более чем пяти простых чисел.

«Надо сказать, что появление работы Тао, посвященной пяти простым числам, подстегнуло меня. У меня появился повод собрать воедино все те идеи, которые на тот момент скопились у меня по поводу тернарной гипотезы Гольдбаха. Результатом этого стала работа, посвященная малым дугам. Еще год ушел у меня на работу по большим дугам», — рассказал Хельфготт.

«Я помог Платту, — говорит Хельфготт, — выбил ему время на суперкомпьютерах в разных местах. Впрочем, его вычисления нужны не только в этой задаче — они будут полезны и в других разделах математики».

Бинарная проблема Гольдбаха

Еще одним интересным результатом является теорема Чена — она утверждает, что всякое четное число представимо либо в виде суммы двух простых, либо в виде суммы простого и полупростого (числа, состоящего из произведения двух простых).

Этот результат неоднократно улучшался — в 1995 году Оливер Рамаре показал, что всякое четное число представимо в виде суммы не более, чем шести простых. Примечательно, что новый результат Хельфготта позволяет улучшить результат Рамаре: вычитая из четного числа тройку, мы получаем нечетное, которое, как теперь известно, представимо в виде суммы трех простых. Стало быть, всякое четное число представимо в виде суммы четырех простых.

Сами же математики считают, что решение сильной проблемы Гольдбаха еще далеко.

Источник