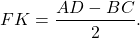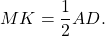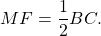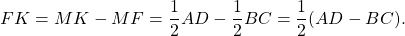Докажите что отрезок соединяющий середины диагоналей трапеции параллелен ее

Отрезок, соединяющий середины диагоналей трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции

1) лежит на средней линии трапеции,

2) равен полуразности оснований трапеции.

Дано: ABCD — трапеция, AD||BC,

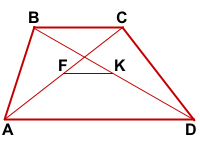
F — середина AC, K — середина BD,

MN — средняя линия трапеции

Так MN — средняя линия трапеции ABCD, то M — середина AB, N — середина CD, и MN||AD, MN||BC.

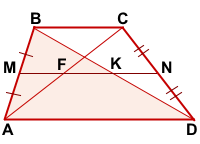
Рассмотрим угол ABD.

Так как AM=BM и MN||AD, то по теореме Фалеса, отрезки, на которые прямая MN делит BD, также равны, то есть MN пересекает отрезок BD в его середине, то есть в точке K.

Аналогично, для угла BAC:

AM=BM, MN||AD, следовательно, по теореме Фалеса прямая MN пересекает отрезок AC в его середине, то есть в точке F.

Таким образом, отрезок, соединяющий середины диагонали трапеции, параллелен основаниям трапеции и лежит на её средней линии.

MF — средняя линия треугольника ABC. Поэтому

Что и требовалось доказать.

Если использовать обозначения AD=a, BC=b, то формула длины отрезка, соединяющего середины диагоналей трапеции, примет вид

Источник

Отрезок соединяющий середины диагоналей трапеции

Здравствуйте!
Нужно доказать, что отрезок, соединяющий середины диагоналей трапеции, расположен параллельно относительно ее оснований и численно равен половине их разности.
Спасибо!

Отрезок, соединяющий середины диагоналей трапеции
У трапеции есть интересное свойство, которое объединяет сразу три ее основные измерения: диагонали, основания и среднюю линию:
Отрезок, которые соединяет середины диагоналей, принадлежит средней линии, а его длина равна разности оснований трапеции, деленной на 2.
В школьном курсе геометрии предлагается решить такую задачу:
Доказать, что отрезок, который соединяет середины диагоналей трапеции, расположен параллельно относительно ее оснований и численно равен половине их разности.
Рассмотрим доказательство этой задачи.
Итак, дана трапеция, назовем которую стандартно — ABCD.
Обозначим середину диагонали АС точкой М, а середину диагонали BD точкой N. Следовательно, АМ = МС и BN = ND.
Докажем, что:
1) прямая, которая содержит отрезок MN, параллельна основанию трапеции AD;
2) .

Доказательство:
Воспользуемся теоремой Фалеса.
Рассмотрим треугольники АВС и ВСD.
Средняя линия трапеции KF проходит через средины сторон АВ и CD, а также через середины диагоналей AC и BD. Следовательно отрезок MN, который также проходит через середины М и N диагоналей трапеции, лежит на прямой KF. Прямая KF по свойству средней линии трапеции параллельна ее основаниям. Значит, отрезок MN также параллелен основанию AD. Что и требовалось доказать.
Воспользуемся еще одним свойством средней линии трапеции, согласно которому она равна половине суммы оснований трапеции.
Рассмотрим треугольник АСD.
В нем средней линией является отрезок MF. Запишем:

Рассмотрим треугольник BСD.
В нем средней линией является отрезок NF. Запишем:

Отрезок MN можно найти путем вычитания из отрезка MF отрезка NF:
MN = MF — NF.
Подставим в формулу выражения для MF и NF:

Теорема доказана.

Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Источник