Докажите что отрезок соединяющий середины сторон треугольника параллелен третьей стороне

Докажите что отрезок соединяющий середины сторон треугольника параллелен третьей стороне

§ 48. СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА

Теорема. Отрезок,соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и равен ее половине.

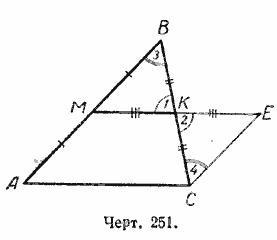
Доказательство. Продолжим МК на отрезок КЕ = МК и точку С соединим с точкой Е (черт. 251).

Рассмотрим треугольники МВК и КЕС.

СК = КВ — по условию,
КЕ = МК — по построению,
/ 1 = / 2, как вертикальные
Следовательно /\ МВК = /\ КЕС

Из равенства этих треугольников следует:
1) ЕС = МВ и, значит, ЕС = АМ;
2) / 4 = / 3, но это углы внутренние накрест лежащие при прямых ЕС и МВ и секущей ВС, следовательно, ЕС || МВ и, значит, ЕС || АМ.

Рассмотрим теперь четырёхугольник АМЕС. В нем ЕС = АМ и ЕС || АМ, поэтому
АМЕС — параллелограмм (§ 43, п. 3).

1) МЕ || АС и, значит, МК ||АС,
2) МЕ = AС и, значит, МК = AC /₂

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

1. Доказать, что прямая, проходящая через середину какой-либо стороны треугольника параллельно другой его стороне, делит третью сторону треугольника пополам.

2. Доказать, что отрезки, соединяющие последовательно середины сторон любого четырёхугольника, образуют параллелограмм.

Указание. Провести в четырёхугольнике диагонали.

3. Диагонали четырёхугольника равны 38 мм и 36 мм. Вычислить периметр параллелограмма, образованного отрезками, соединяющими середины сторон этого четырёхугольника.

Источник

Средняя линия треугольника

Определение 1. Средней линией треугольника называется отрезок, соединяющий середины двух сторон.

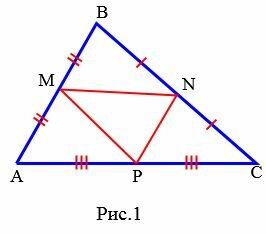У треугольника три средние линии. На Рис.1 отрезки MN, NP, MP являются средними линиями треугольника.

Теорема 1. Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.

Доказательство. Пусть MN средняя линия треугольника ABC (Рис.2). Докажем, что \( \small MN || AC, \) \( \small MN=\frac12 AC. \)

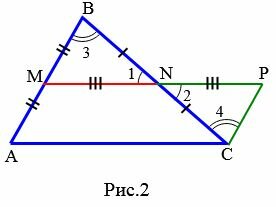Далее, поскольку точка M является серединой отрезка AB, имеем : AM=MB. Но \( \small MB=CP \) и, следовательно AM = CP. Получили что в четырехугольнике AMPC стороны AM и CP параллельны и равны. Тогда по признаку 1 статьи Параллелограмм четырехугольник AMPC является параллелограммом. Отсюда следует, что MP || AC или MN ||AC.

Остается показать, что \( \small MN=\frac12 AC. \) Так как MN=NP, то \( \small MN=\frac12 MP. \) Но в параллелограмме MP = AC. Тогда \( \small MN=\frac12 AC. \)

Источник

Как найти третью сторону треугольника — формулы и расчеты

В геометрии первая фигура, которую школьники начинают изучать, это треугольник. Он является одним из самых распространенных и простых замкнутых объектов. Знание свойств фигуры и необходимых теорем позволяет решать разные задачи о том, как найти третью сторону треугольника на плоскости.

Фигура из шести элементов

Под геометрическим элементом полагают какой-либо объект, который имеет определенную меру и является составляющей частью некоторой фигуры. Например, для сферы основными образующими элементами являются радиус и центр.

Как известно, треугольник — это фигура, которая состоит из трех отрезков и такого же количества вершин. При этом все отрезки попарно пересекаются. Из определения фигуры следует, что ее образуют два типа элементов, общее количество которых составляет 6:

Обычно треугольник обозначают большими латинскими буквами, например, ABC, PQM и так далее. Каждая буква — это название вершины (точка пересечения двух отрезков). AB, BC и CA, которые являются длинами сторон, принято обозначать маленькими латинскими буквами по названию противоположных им вершин, то есть c, a и b, соответственно.

Дополнительные отрезки

Несмотря на всю простоту построения фигуры, она обладает большим количеством дополнительных элементов, которые ее могут определять. Среди них самыми важными являются следующие:

Виды треугольников

Разработана достаточно развитая классификация рассматриваемых фигур. Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:

Основные свойства и понятия

Треугольник является одной из самых изученных фигур в геометрии. Для него известны многие теоремы, которые с успехом используются при решении задач. Существует два основных свойства фигуры, которые следуют из характеристик евклидового пространства:

Помимо названных свойств, следует знать о треугольнике еще такое понятие, как подобие. Его суть состоит в том, что одна из рассматриваемых фигур является точной копией в миниатюре другой. Для подобных треугольников все углы равны попарно, а все три стороны относятся соответственно попарно друг к другу с одним и тем же коэффициентом подобия.

Еще одной полезной характеристикой рассматриваемой фигуры является ее качество (CT). Вычисляется оно по следующей формуле:

CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).

Величина CT лежит в пределах от 0 до 1. Она показывает степень близости фигуры к равностороннему, то есть к наиболее симметричному объекту. Если CT 0,5, то фигура характеризуется, как имеющая хорошее качество.

Величина CT применяется для алгоритмов, которые разделяют какую-либо изучаемую геометрическую поверхность на сетку треугольников. Если в этой сетке генерируется много низкокачественных фигур, то будет велика ошибка аппроксимации рассматриваемой величины.

Важные теоремы

Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:

К этим двум теоремам следует добавить еще два важных равенства, которые связаны с именами древнегреческих философов.

Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:

Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.

Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:

Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.

Примеры решения задач

После того как изучены и рассмотрены основные понятия, свойства и теоремы для различного рода треугольников, можно переходить к решению геометрических задач. Поскольку для этого требуется в большинстве случаев знать значения тригонометрических функций, рекомендуется воспользоваться либо соответствующими таблицами, либо инженерным калькулятором.

Задачи школьного курса с треугольниками, как правило, не являются сложными. Они решаются благодаря однократному применению какого-либо свойства или теоремы.

Квадрат и его диагональ

Пусть дан квадрат, сторона которого составляет 11 см. Необходимо определить половину длины его диагонали.

Эту геометрическую задачу проще всего решить, если увидеть, что две смежные стороны исходной фигуры и ее диагональ образуют прямоугольный треугольник, который к тому же является равнобедренным. Каждая из равных сторон в нем имеет длину 11 см и является катетом. Диагональ c — это гипотенуза. Применяя пифагорову теорему, можно получить следующее равенство:

c = (11 2 + 11 2 )^0,5 ≈ 15,556 см.

Поскольку половина диагонали в два раза меньше гипотенузы, то искомым ответом на задачу будет число c/2 ≈ 7,778 см.

Две высоты и угол

Дан треугольник ABC. Известно, что при вершине C угол составляет 37 °. Из вершин A и B проведены высоты к сторонам этого треугольника, их длины составляют h1 = 10 см и h2 = 8 см, соответственно. Необходимо узнать длину стороны фигуры, которая лежит против угла C.

Из условия задачи можно найти длины сторон AC и BC. Для этого следует увидеть, что каждая из высот с двумя другими сторонами треугольника образует прямоугольную фигуру. Воспользовавшись тригонометрическими равенствами, можно получить следующие результаты:

Против угла C лежит сторона AB, которую следует найти. Получается, что известны две стороны треугольника (AC и BC) и угол между ними. Остается применить теорему косинусов, чтобы получить ответ:

AB = (AC 2 + BC 2 — 2*AC*BC*cosC)^0,5 = (16,616 2 + 13,293 2 — 2* 16,616 * 13,293 *cos (37 °))^0,5 ≈ 10 см.

Полученный результат свидетельствует о том, что высота h1 совпадает со стороной AB с рассчитанной точностью, то есть исходный треугольник являлся прямоугольным.

Таким образом, для нахождения стороны треугольника, если известны две другие его стороны или иные отрезки, следует воспользоваться теоремами. Основными из них являются теорема косинусов и синусов, а также Пифагора и Аполлония.

Источник

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Определение и признаки средней линии треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Следствия из теоремы с доказательствами

Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

Следствие №2

Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.

Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Пример решения задачи

Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

Источник

Планиметрия. Страница 4

1.Параллелограмм

Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом.

Рис.1 Теорема. Параллелограмм.

Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам.

Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2)

Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.

Пример 1

Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. (Рис.9)

Доказательство:

Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей.

Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные.

Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны.

Рис.9 Задача. Через точку пересечения диагоналей.

Пример 2

Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10)

Решение:

Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение:

Рис.10 Задача. Две стороны параллелограмма.

Пример 3

В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11)

Решение:

P_ABCD = 2*(х + 2y) = 4, P_ABD = 2x +2y = 3

Рис.11 Задача. В параллелограмме ABCD перпендикуляр.

Пример 4

В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.(Рис.12)

Решение:

Отсюда следует, что FE = AD = 8-х, а BD = х.

Теперь можно составить следующее соотношение:

Периметр прямоугольника ADEF равен 16 см.

Рис.12 Задача. В прямоугольный треугольник.

Пример 5

Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом.(Рис.13)

Доказательство:

Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD.

Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.

Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом.

Рис.13 Задача. Докажите, что если у параллелограмма.

Источник

• ← Докажите что отрезок соединяющий середины сторон параллелограмма
• Докажите что отрезок соединяющий середины →

Главная > Учебные материалы > Математика: Планиметрия. Страница 4
Рис.2 Теорема. Свойство диагоналей параллелограмма. 3.Ромб Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.	Рис.3 Теорема. Свойство диагоналей ромба. Задача В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4)	4.Теорема Фалеса Теорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне.	Рис.5 Теорема Фалеса. 5.Средняя линия треугольника Теорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине.	Рис.5 Теорема. Средняя линия треугольника. 6.Трапеция Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме.	Рис.6 Теорема. Средняя линия трапеции. 7.Теорема о пропорциональных отрезках Теорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки. Доказательство. Пусть дан угол и пересекающие его параллельные прямые. Необходимо доказать, что AС 1 /AС = AВ 1 /AВ (Рис. 7).	Рис.7 Теорема о пропорциональных отрезках. Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС 2 = АС*АВ 1 /АВ.	Рис.8 Теорема о пропорциональных отрезках.