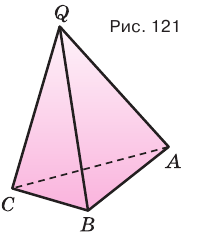
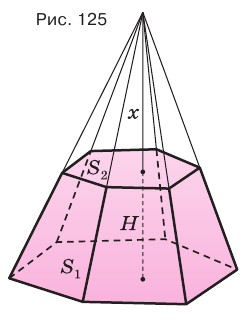
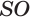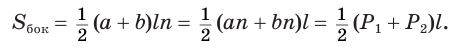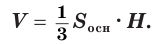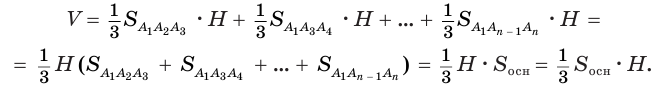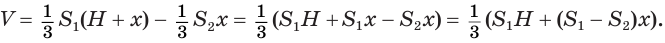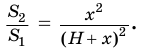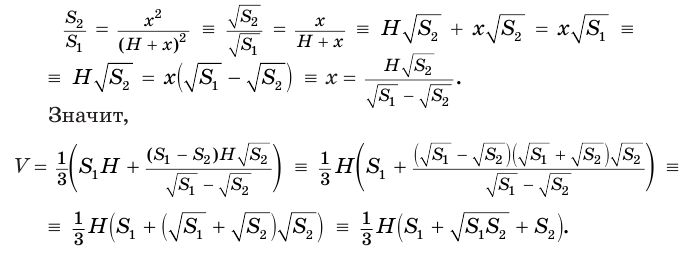Докажите что плоскость пересекающая пирамиду и параллельная ее основанию отсекает подобную пирамиду
T е о р е м а 19.5. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.
Доказательство. Пусть S — вершина пирамиды, А — вершина основания и А’— точка пересечения секущей плоскости с боковым ребром SA (рис. 23). Подвергнем пирамиду преобразованию гомотетии относительно вершины S с коэффициентом гомотетии
При этой гомотетии плоскость основания переходит в параллельную плоскость, проходящую через точку А’, т. е. в секущую плоскость, а следовательно, вся пирамида — в отсекаемую этой плоскостью часть. Так как гомотетия есть преобразование подобия, то отсекаемая часть пирамиды является пирамидой, подобной данной. Теорема доказана.
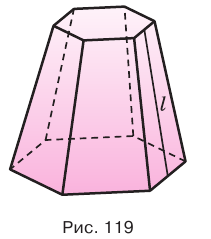
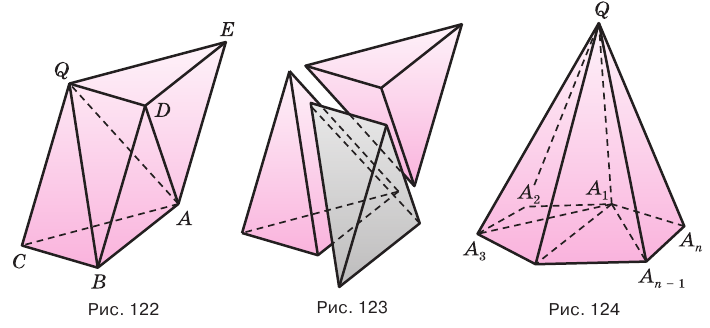
По теореме 19.5 плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой (рис. 24). Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные (более того, гомотетичные) многоугольники, боковые грани — трапеции.
14. Правильная пирамида
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани — равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды, проведенная из её вершины, называется апофемой. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Докажите что плоскость пересекающая пирамиду и параллельная ее основанию отсекает подобную пирамиду
Ключевые слова: пирамида, многогранник, правильная пирамида, грань, объем, боковая поверхность
Многогранник, у которого одна грань, называемая основанием, – многоугольник,
а другие грани – треугольники с общей вершиной, называется пирамидой.
Грани, отличные от основания, называются боковыми.
Общая вершина боковых граней называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми.
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание.
Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.
Плоскость, параллельная основанию пирамиды, отсекает ее на подобную пирамиду и усеченную пирамиду.
Если все боковые ребра равны, то
Если боковые грани наклонены к плоскости основания под одним углом, то
См. также:
Усеченная пирамида
«Многогранники» (стр. 3 из 3)
На рисунке 22 построено сечение четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из ее боковых ребер.
13. Усеченная пирамида
T е о р е м а 19.5. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.
Доказательство. Пусть S — вершина пирамиды, А — вершина основания и А’— точка пересечения секущей плоскости с боковым ребром SA (рис. 23). Подвергнем пирамиду преобразованию гомотетии относительно вершины S с коэффициентом гомотетии
При этой гомотетии плоскость основания переходит в параллельную плоскость, проходящую через точку А’, т. е. в секущую плоскость, а следовательно, вся пирамида — в отсекаемую этой плоскостью часть. Так как гомотетия есть преобразование подобия, то отсекаемая часть пирамиды является пирамидой, подобной данной. Теорема доказана.
По теореме 19.5 плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой (рис. 24). Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные (более того, гомотетичные) многоугольники, боковые грани — трапеции.
14. Правильная пирамида
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани — равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды, проведенная из её вершины, называется апофемой. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Т е о р е м а 19.6. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Доказательство. Если сторона основания а, число сторон п, то боковая поверхность пирамиды равна:
где I — апофема, a p — периметр основания пирамиды. Теорема доказана.
Усеченная пирамида, которая получается из правильной пирамиды, также называется правильной. Боковые грани правильной усеченной пирамиды — равные равнобокие трапеции; их высоты называются апофемами.
15. Правильные многогранники
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер. )
Существует пять типов правильных выпуклых многогранников (рис.25): правильный тетраэдр (1), куб (2), октаэдр (3), додекаэдр (4); икосаэдр (5).
У правильного тетраэдра грани — правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
У куба все грани — квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.
У октаэдра грани — правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
У додекаэдра грани — правильные пятиугольники. В каждой вершине сходится по три ребра.
III. Практическая часть.
Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА\ и ВВ\ на ребро угла. Найдите длину отрезка АВ, если АА1=а, ВВ1=b, А1В1=с и двугранный угол равен а (рис. 26).
По теореме Пифагора
У трехгранного угла (abc) двугранный угол при ребре с прямой, двугранный угол при ребре b равен j, а плоский угол (bс) равен g (j, g
Из прямоугольных треугольников ОАВ, ОСВ, АОС и АВС получаем:
tg a =AB/OB=(BC/ cos j)/(BC/tg g)= tg g/ cos j
tg b =AC/OC=BC tg j / (BC/sin g)= tg g sin g
В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если
Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 28). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.
Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400 см2. Найдите площади сечений.
Докажите, что боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Решение. Боковые грани усеченной пирамиды — трапеции с одним и тем же верхним основанием а, нижним b и высотой (апофемой) l. Поэтому площадь одной грани равна ½ (а + b)l. Площадь всех граней, т. е. боковая поверхность, равна ½ (аn + bn)l, где n — число вершин у основания пирамиды, an и bn — периметры оснований пирамиды.
Благодаря этой работе я обобщила и систематизировала знания, полученные за курс обучения в 11 классе, ознакомилась с правилами выполнения творческой работы, получила новые знания и применила их на практике.
Мне бы хотелось чаще использовать свои новые полученные знания на практике.
1. А.В. Погорелов «Геометрия». – М.: Просвещение, 1992
3. Л.Д. Кудрявцев «Курс математического анализа» т.1, Москва 1981
4. Л.Ф. Пичурин «За страницами учебника геометрии». – М.: Просвещение, 1990
Стереометрия. Страница 5
| Главная > Учебные материалы > Математика: Стереометрия. Страница 5 | ||
 | ||
 | ||
| 1.Двугранный, трехгранный углы. 2.Призма и построение ее сечений. 3.Параллелепипед. 4.Прямоугольный параллелепипед. 5.Пирамида. 6.Усеченная пирамида. 7.Правильные многогранники. 8.Примеры. | ||
1. Двугранный, трехгранный углы
Если провести плоскость, перпендикулярную ребру двугранного угла, то она пересечет его грани по двум полупрямым. Угол, образованный между двумя этими полупрямыми, называется линейным углом двугранного угла.
Градусная мера двугранного угла равна градусной мере линейного угла. Величина двугранного угла не зависит от выбора линейного угла, т.е. плоскости, перпендикулярной ребру двугранного угла.

Рис. 1 Двугранный угол.
Трехгранный углы
Понятие многогранного угла можно определить аналогичным образом.

Рис. 1.1 Трехгранный угол.
2.Призма и построение ее сечений
Прямая призма
Призмой называется многогранник, у которого две стороны являются плоскими многоугольниками, лежащими в параллельных плоскостях и совмещаемых параллельным переносом, а боковые грани состоят из всех отрезков, соединяющих соответствующие точки этих многоугольников (Рис.2). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие точки оснований, ее ребрами.
Высотой призмы называется расстояние между ее основаниями.
Если боковые ребра призмы перпендикулярны основанию, то такая призма называется прямой. В противном случае призма называется наклонной. Боковые ребра у призмы параллельны и равны.
Боковые грани прямой призмы являются прямоугольниками. Если в основании призмы лежит правильный многоугольник, то такая призма называется правильной.
Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на ее высоту.
В основании призмы лежит правильный многоугольник. Боковые ребра призмы находятся под прямым углом к основанию и являются высотами. Боковые грани представляют собой прямоугольники. Отсюда следует, что площадь боковой поверхности призмы равна:
Полная площадь призмы равна сумме площадей двух оснований и боковой поверхности.
Рис.2 Прямая призма
Наклонная призма
Если боковые ребра призмы находятся под некоторым углом к основанию, то призма является наклонной (Рис.2.1).
Используя правила параллельного проектирования, изображение призмы можно построить следующим образом. Сначала строится одно из оснований, т.е. многоугольник, а затем проводят боковые ребра из каждой вершины основания, которые параллельны и равны между собой. Затем концы этих отрезков соединяются и строится другое основание призмы.
Для того, чтобы построить сечение призмы плоскостью, сначала задают прямую g в плоскости одного из оснований, которая называется следом. Затем проводят через заданную точку В прямую, которая находится в плоскости грани, и соединяют ее с заданным следом в точке Е. Отрезок АС на рассматриваемой грани есть пересечение этой грани с секущей плоскостью.
Если грань, которая содержит точку В, параллельна следу, то секущая плоскость пересекает эту грань по отрезку, параллельному заданному следу и проходящему через точку В.
Таким образом, можно провести отрезки на всех гранях призмы и получить сечение плоскостью с заданным следом.
Рис.2.1 Наклонная призма
3. Параллелепипед
Призма, у которой основание есть параллелограмм, называется параллелепипедом.
Теорема. Противолежащие грани параллелепипеда параллельны и равны.
Доказательство. Пусть дан параллелепипед ABCDA’B’C’D’ (Рис.3). Рассмотрим грани параллелепипеда AA’D’D и BB’C’C. Так как основания параллелепипеда параллелограммы, то сторона AD параллельна и равна стороне ВС, а сторона A’D’ параллельна и равна стороне B’C’. Сторона AB параллельна и равна стороне DС, а сторона A’B’ параллельна и равна стороне D’C’. Отсюда можно сделать вывод, что грани AA’D’D и BB’C’C лежат в параллельных плоскостях. Таким образом, грань AA’D’D совмещается параллельным переносом с гранью BB’C’C. Следовательно эти грани равны.
Аналогично можно доказать параллельность и равенство граней DD’C’C и AA’B’B.
Центральная симметрия параллелепипеда
Теорема. Диагонали параллелепипеда пересекаются в одной точке, которая делит их пополам.
Отсюда следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии.
Рис. 3 Наклонный параллелепипед.
4.Прямоугольный параллелепипед
Прямой параллелепипед, у которого основание является прямоугольником, называется прямоугольным.
Длины не параллельных ребер параллелепипеда называются его линейными размерами.
Теорема. В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех его измерений.
Доказательство. Пусть дан параллелепипед ABCDA’B’C’D’ (Рис.4). Рассмотрим прямоугольный треугольник ACC’. Cторонами данного треугольника являются диагональ параллелепипеда AC’, диагональ основания AC и ребро боковой грани CC’. Тогда по теореме Пифагора находим:
Рис. 4 Прямоугольный параллелепипед.
AC 2 = AD 2 + DC 2 Следовательно:
AC’ 2 = AD 2 + DC 2 + CC’ 2
Стороны AD, DC, CC’ являются линейными размерами параллелепипеда.
Симметрия прямоугольного параллелепипеда
Прямоугольный параллелепипед имеет центр симметрии. Если все три измерения параллелепипеда разные, то он имеет три плоскости симметрии, которые проходят через центры граний (Рис.4.1)
Если параллелепипед имеет два равных измерения, то у него есть еще две плоскости симметрии, которые проходят через диагональные сечения.
Если у параллелепипеда все три линейные размера равны, то он является кубом. И у него девять плоскостей симметрии.
Рис. 4.1 Симметрия прямоугольного параллелепипеда.
5. Пирамида
Пирамидой называется многогранник, который состоит из многоугольника в основании, точки, не лежащей в плоскости основания, и всех отрезков, соединяющих вершины многоугольника и данную точку (Рис.5).
Точка, не лежащая в плоскости основания, называется вершиной пирамиды.
Отрезки, соединяющие вершины основания с вершиной пирамиды, называются боковыми ребрами.
Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется высотой пирамиды.
На рисунке 5 изображена пирамида, в основании которой лежит правильный шестиугольник. A1A2A3A4A5A6
Построение пирамиды и ее плоских сечений
Если точка В лежит на грани, параллельной следу g (Рис.5.1), то секущая плоскость пересекает эту грань по отрезку BC, параллельному следу g. Концы отрезка также соединяют со следом по прямой ED в плоскости α другой грани и получают прямую пересечения этой грани с плоскостью сечения и т.д. Таким образом можно построить линии пересечения плоскости сечения со всеми гранями пирамиды.
Рис. 5.1 Построение пирамиды и ее плоских сечений.
6. Усеченная пирамида
Теорема. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.
Правильная пирамида
Если основание пирамиды есть правильный многоугольник, а основание высоты совпадает с центром этого многоугольника, то такая пирамида называется правильной.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Рис. 6 Усеченная пирамида.

7. Правильные многогранники
Если выпуклый многогранник имеет все грани правильные многоугольники с равным числом сторон и в каждой вершине многоугольника сходится одно и то же число ребер, то такой многогранник называется правильным.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр это многогранник, у которого грани правильные треугольники.
Додекаэдр это многогранник, у которого грани правильные пятиугольники. В каждой вершине сходится по три ребра.
Икосаэдр это многогранник, у которого грани правильные треугольники. В каждой вершине сходится по пять ребер.
Рис. 6 Правильные многогранники.

8. Пример 1
Докажите, что сечение призмы, параллельное основаниям, равно основаниям.
Доказательство:
Пусть дана призма АВСA’B’C’ (Рис.7). Основания призмы равны и являются треугольниками. Они лежат в параллельных плоскостях и совмещаются параллельным переносом. Отсюда следует, что боковые ребра параллельны и равны.
Отсюда следует, что A»C» = AC, A»B» = AB, B»C» = BC. Таким образом, треугольник A»B»C» равен треугольнику АВС и A’B’C’ соответственно. Отсюда можно сделать и общий вывод: если в основании призмы будет лежать како-либо многоугольник, то в сечении, параллельном основаниям, получится такой же многоугольник.
Рис.7 Задача. Докажите, что сечение призмы.
Пример 2
Боковое ребро наклонной призмы равно 16 м. Оно наклонено к плоскости основания под углом 30°. Найдите высоту призмы.
Решение:
Рассмотрим треугольник AA’P. Угол A’AP равен 30° по условию задачи. Опустим высоту A’O. В прямоугольном треугольнике AA’O найдем A’O.
A’O = AA’ sin 30° = 16 / 2 = 8 м.
Рис.8 Задача. Боковое ребро наклонной призмы равно 15 м.
Пример 3
В правильной четырехугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковые ребра и наклоненная к плоскости основания под углом 60°. Сторона основания равна 8 м. Найдите площадь полученного сечения.
Решение:
Пусть дана правильна четырехугольная призма АВСDA’B’C’D’ (Рис. 9). Заметим, что многоугольник PBCDF является проекцией многоугольника PKHSF на плоскость основания, площадь которого необходимо найти. Следовательно, найдем площадь многоугольника PBCDF.
Теперь найдем площадь многоугольника PKHSF из формулы:
SPKHSF = SPBCDF / cos 60° = 56 / 1 / 2 = 112 м 2
Рис.9 Задача. В правильной четырехугольной призме.
Пример 4
Решение:
Пусть дана правильная четырехугольная призма АВСDA’B’C’D’ (Рис. 10). Так как призма имеет четыре боковые грани, то площадь одной боковой грани составляет 1/4 часть боковой поверхности.
SAA’D’D = Sбок / 4 = 12 / 4 = 3 м 2
Площадь основания призмы равна половине разности площадей между полной поверхностью призмы и ее боковой поверхностью.
Следовательно, высота призмы составляет 3 / 2 м.
Рис.10 Задача. Боковая поверхность правильной четырехугольной призмы.
Пример 5
Решение:
По теореме Пифагора найдем боковые ребра SA и SD:
SA 2 = AO 2 + SO 2 = 4 2 + 7 2 = 65
SD 2 = OD 2 + SO 2 = 3 2 + 7 2 = 58
SA = 
Теперь найдем сторону ромба AD:
Теперь по теореме косинусов найдем косинус угла α между боковыми ребрами:
Отсюда, cos α = 49 / 
Теперь найдем площадь боковой грани SASD:
SASD = SA SD sin α / 2 = 

Отсюда, Sбок = 4 SASD = 4 * 18.5 = 74 м 2
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
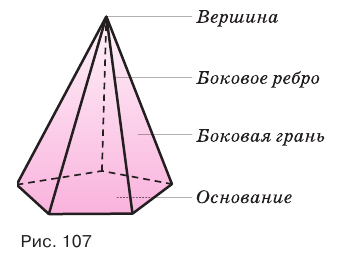
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
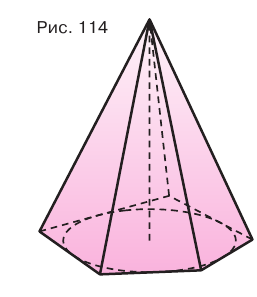
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота
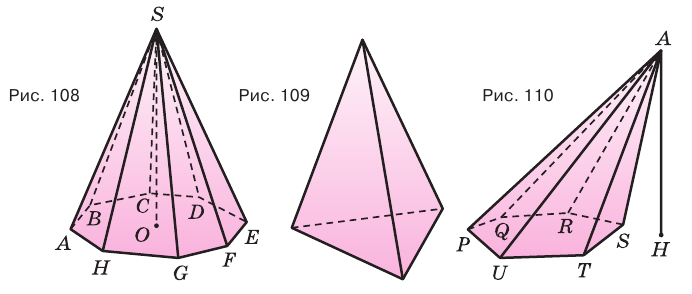
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
Отметим, что если в пирамиде равны все:
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
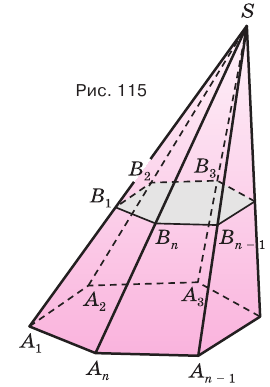
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
Используя рисунок 115, докажите эту теорему самостоятельно.
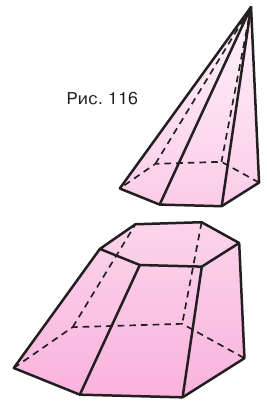
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
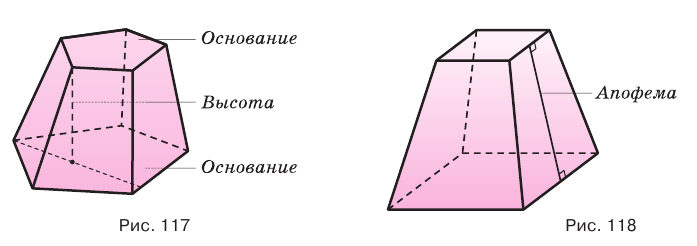
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
Доказательство:
Пусть есть правильная 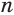
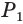
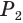
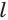
Боковая поверхность данной пирамиды состоит из 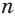
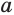
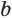
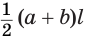
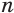
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
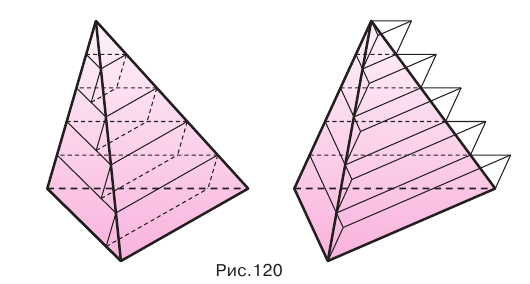
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 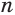
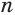
Пусть 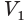
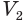


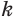
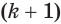


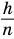
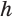
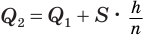
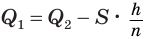
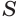
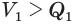
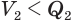
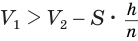
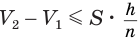
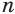
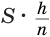
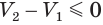
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что 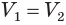
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
Доказательство:
Пусть есть треугольная пирамида 

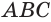
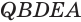
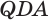


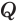
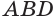
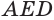




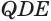

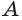
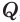





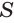

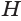



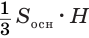
Пусть теперь есть произвольная пирамида 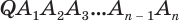
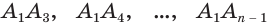
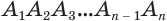
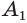
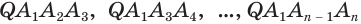

Пример:
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 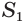
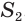

Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 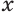
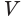
Чтобы найти высоту 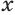
Решим это уравнение, учитывая, что 

Таким образом, объем 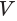


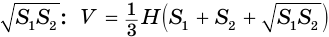
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
- Докажите что плоскости проходящие через точки ad1b1 и c1bd куба abcda1b1c1d1 параллельны
- Докажите что плоскость перпендикулярная к прямой по которой пересекаются две данные плоскости