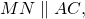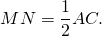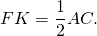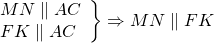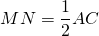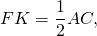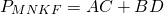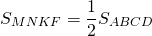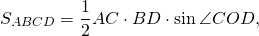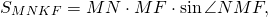Докажите что середины сторон пространственного четырехугольника
Теорема Вариньона
В школьном курсе теорема Вариньона часто фигурирует в качестве обычной задачи, в которой требуется доказать, что середины сторон четырёхугольника являются вершинами параллелограмма.
Её доказательство основано на свойствах средней линии треугольника.
Середины сторон четырёхугольника являются вершинами параллелограмма.

M, N, K, F — середины его сторон.
Доказать : MNKF — параллелограмм.

2) Рассмотрим треугольник ABC.
Так как точки M и N — середины сторон AB и BC, отрезок MN — средняя линия треугольника ABC.
3) Аналогично, FK — средняя линия треугольника ADC и
4) По признаку параллельности прямых, две прямые, параллельные третьей прямой, параллельны между собой:
5) В четырёхугольнике MKNF противоположные стороны параллельны и равны. Следовательно, MKNF — параллелограмм (по признаку).
Что и требовалось доказать.
Поскольку в школьном курсе геометрии рассматриваются только выпуклые четырёхугольники, доказательство приведено только для этого случая. Но и для невыпуклых четырёхугольников (в том числе, и для самопересекающихся), теорема также верна (доказывается аналогично).
Параллелограмм, образованный серединами сторон четырёхугольника, называется параллелограммом Вариньона (вариньоновским, вариньоновым).
Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма:
(так как стороны MNKF равны половине диагонали AC или BD).
Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма:
углы COD и NMF равны (как внутренние накрест лежащие при параллельных прямых AC и MN и секущей BD),
Презентация была опубликована 8 лет назад пользователемНина Толстоброва
Похожие презентации
Презентация на тему: » Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма. А В СFS LND.» — Транскрипт:
2 Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма. А В СFS LND
3 Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Определение М a b a b
4 IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.
6 Найдите на рисунке параллельные прямые. Назовите параллельные прямые и плоскости. Найдите скрещивающиеся прямые.
8 а II b а II b Три случая взаимного расположения двух прямых в пространстве а b а bМa b a b a b
10 А D С В B1B1 С1С1 D1D1 А1А1 Каково взаимное положение прямых 1) AD 1 и МN; 2) AD 1 и ВС 1 ; 3) МN и DC? N M
11 А D С В B1B1 С1С1 D1D1 А1А1 Докажите, что прямые 1) AD и C 1 D 1 ; 2) A 1 D и D 1 C; 3) AB 1 и D 1 C скрещивающиеся. N M
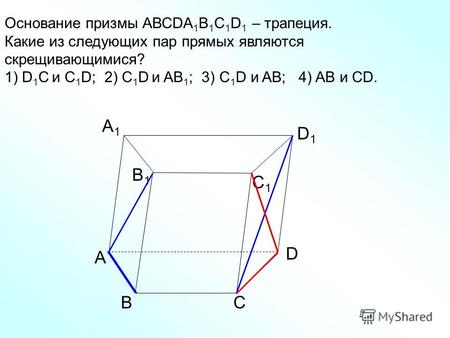
12 А D СВ B1B1 С1С1 D1D1 А1А1 Основание призмы АВСDA 1 B 1 C 1 D 1 – трапеция. Какие из следующих пар прямых являются скрещивающимися? 1) D 1 C и C 1 D; 2) C 1 D и AB 1 ; 3) C 1 D и AB; 4) AB и CD.
13 Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теорема о скрещивающихся прямых D С B E A
14 полуплоскость граница Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. а
15 Углы с сонаправленными сторонами A О О1О1О1О1 О2О2О2О2 A1A1A1A1 В2В2В2В2 A2A2A2A2 О3О3О3О3 A3A3A3A3
16 Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами О О1О1О1О1 A1A1A1A1 A B1B1B1B1 B
18 a b 30 0 n m Угол между прямыми m и n Угол между прямыми а и b 30 0.
19 Угол между скрещивающимися прямыми а b а ba bb М Через произвольную точку М 1 проведем прямые m и n, соответственно параллельные прямым a и b. Угол между скрещивающимися прямыми a и b равен mn
20 Угол между скрещивающимися прямыми а b а ba b М Точку М можно выбрать произвольным образом. m В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.
23 т Прямая m параллельна диагонали ВD ромба АВСD и не лежит в плоскости ромба. Докажите, что а) m и АС – скрещивающиеся прямые – и найдите угол между ними; б) m и AD – скрещивающиеся прямые – и найдите угол между ними, если АВС = А В D С 128 0
24 АD С А1А1 B1B1 С1С1 D1D1 В На рисунке АВСD – параллелограмм, АВС = 130 0, АА 1 II BB 1 II CC 1 II DD 1 и АА 1 = BB 1 =CC 1 =DD 1. Найдите угол между прямыми АВ и А 1 D 1. Рассмотрите различные способы.
25 АD С А1А1 B1B1 С1С1 D1D1 В На рисунке АВСD – параллелограмм, ВСC 1 = 120 0, АА 1 II BB 1 II CC 1 II DD 1 и АА 1 = BB 1 =CC 1 =DD 1. Найдите угол между прямыми ВВ 1 и АD.
Докажите что середины сторон пространственного четырехугольника
Нужно решить первое и четвертое
Задача (11) (решена в учебнике Погорелова). Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма (вершины пространственного четырехугольника не лежат в одной плоскости).
Пусть ABCD — данный пространственный четырехугольник (рис. 326). Пусть А1, В1, С1, D1 — середины его сторон. Тогда A1B1 — средняя линия треугольника АBС, параллельная стороне АС, C1D1—средняя линия треугольника ACD, тоже параллельная стороне АС.
По теореме 16.2 прямые A1B1 и C1D1 параллельны, а значит, лежат в одной плоскости. Точно так же доказывается параллельность прямых A1D1 и B1C1.
Итак, четырехугольник A1B1C1D1 лежит в одной плоскости и его противолежащие стороны параллельны. Следовательно, он параллелограмм.
Условие задачи: 4. Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и CD, АС и BD, AD и BC, пересекаются в одной точке.
Пусть точки M, N, K, L, P, Q — середины отрезков AB, BC, CD, AD, BD, AC соответственно.
Из задачи №11 получаем, что отрезки МК и NL являются диагоналями параллелограмма MNKL с вершинами в серединах сторон четырехугольника ABCD. Значит, МК и NL пересекаются в некоторой точке O и делятся этой точкой пополам. Также отрезки PQ и NL являются диагоналями параллелограмма PNQL с вершинами в серединах сторон четырехугольника ABCD, образованного этими сторонами. Значит, PQ и NL пересекаются и в точке пересечения делятся пополам, а так как O — середина NL, то, значит, O — середина PQ. И PQ и NL пересекаются в точке O. Так что искомые прямые MK, NL и PQ, соединяющие середины отрезков AB и CD, BC и AD, AC и BD соответственно пересекаются в одной точке O, что и требовалось доказать.