Докажите что существует булева функция которую нельзя выразить формулой со связками и
Представление булевой функции формулой логики высказываний
Булевы функции.
DEF. Булевой функцией f( 

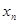
Таким образом, все аргументы булевой функции (Б.ф.) принимают значения из множества <0;1>и сама функция принимает значения из этого же множества.
Всякую булеву функцию можно задать таблицей. Если f зависит от n переменных в таблице будет 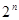
Например, для случая n=2 булеву функцию можно задать таблицей:
Пример: Если f(x), то n=1. Тогда 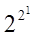
| x | f1 | f2 | f3 | f4 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| Б.ф. | 0 | 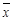 | 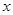 | 1 |
Очевидно, что каждой формуле логики высказываний можно поставить в соответствие булеву функцию, причем если формуле 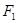
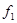
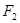
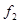
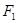
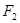
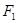
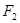
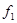
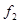
Докажем, что формулы алгебры логики дают все булевы функции. Для этого сформулируем:
DEF. 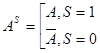
(т.е. при 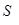
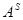
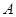
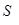
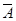
При этом с каждым набором переменных будем ассоциировать элементарную конъюнкцию 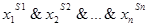
Действительно, возможны два случая:
1) если 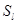
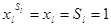
2) если 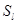
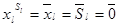
Здесь также возможны два случая:
1) 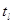
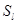
2) 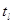
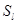
В первом случае: 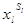
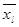
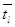
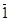
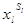
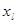
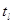
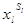
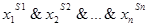
Th: Пусть f( 

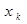


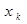
Существование
Пусть функция f( 

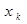
1) f ( 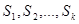
2) f ( 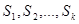
1) Пусть на некотором наборе функция f равна 1, тогда в таблице соответствующая строка находится среди выбранных, а значит, элементарная конъюнкция 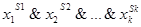
Единственность
Предположим противное: Пусть 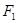
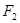
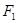
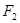
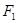
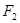
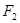
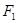
Таким образом, предположение о существовании двух формул неверно – единственность доказана.
 |  | 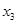 | f | |
| 1 | 1 | 1 | 1 | × |
| 1 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | × |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | × |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 |
F = ( 

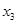

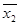
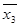
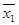

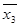
Замечания к теореме:
1. Из доказанной теоремы следует утверждение: для любой не тождественно ложной формулы А существует равносильная ей формула F, находящаяся в совершенной дизъюнктивной нормальной форме. Это утверждение было ранее доказано (формулу F получали с помощью равносильных преобразований). Таким образом, данная теорема дает второй способ получения совершенной дизъюнктивной нормальной формы.
2. Из доказанной теоремы следует утверждение об единственности совершенной дизъюнктивной нормальной формы для любой формулы А: если формула А выражает булеву функцию f, то и любая совершенная дизъюнктивная нормальная форма должна выражать собой ту же функцию, поэтому все совершенные дизъюнктивные нормальные формы должны совпадать с точностью до порядка элементарных конъюнкций.
Аналогично совершенной дизъюнктивной нормальной форме можно рассмотреть совершенную конъюнктивную нормальную форму и для нее справедлива следующая теорема:
Th: Пусть f( 

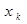


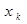
Доказывается аналогично теореме о совершенной дизъюнктивной нормальной форме.
 |  | 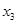 | f | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | × |
| 1 | 0 | 1 | 0 | × |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 0 | × |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | × |
| 0 | 0 | 0 | 0 | × |
Рассмотри все булевы функции от двух переменных.
Если n = 2,то 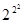
 |  | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 |
| Булева функция |  & &  |  & & 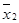 | 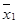 & &  | 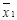 & & 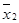 |  |  |  Û Û  | 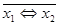 |
 |  | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
| Булева функция | 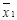 | 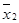 |  Ú Ú  |  Ú Ú 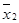 | 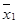 Ú Ú  | 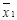 Ú Ú 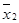 |
Дата добавления: 2016-05-16 ; просмотров: 1279 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Конспект на тему «Булевы функции. Выражение булевых функций через дизъюнкцию, конъюнкцию и отрицание. Теорема Поста»
Содержимое разработки
Предмет: Элементы математической логики.
Тема 47-48. Булевы функции. Выражение булевых функций через дизъюнкцию, конъюнкцию и отрицание. Теорема Поста
Булева функция (или логическая функция, или функция алгебры логики) от n аргументов – в дискретной математике – отображение Bn → B, где B = <0,1>— булево множество. Элементы булева множества <1, 0>обычно интерпретируют как логические значения «истинно» и «ложно».
Выражение булевых функций через конъюнкцию, дизъюнкцию и отрицание Существуют такие булевы функции, через которые выражаются все (вообще все, от любого числа аргументов!) булевы функции. Этим замечательным свойством обладают взятые вместе конъюнкция, дизъюнкция и отрицание. Прежде чем сформулировать и доказать основную теорему этого пункта, обратимся к следующей важной лемме. 
Итак, функции из обеих частей равенства принимают одинаковые значения при одинаковых значениях их аргументов. Следовательно, эти функции равны и доказываемая формула справедлива.
Совершенно аналогично доказывается вторая формула.
Заметим, что подобным образом могут быть записаны формулы разложения булевой функции по любой ее переменной. Запишите, например, такие разложения по последней переменной.
В предыдущем параграфе были рассмотрены некоторые классы булевых функций. В каждый класс попадают функции, обладающие определённым свойством. Для удобства введём следующие обозначения:
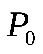

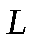
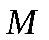
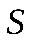
Все перечисленные классы функционально замкнуты.
Теперь докажем критерий полноты.
Теорема 1: (теорема Поста). Для полноты системы функций 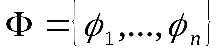
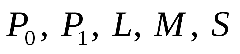
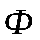
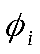
Необходимость условия теоремы следует из того, что если некоторая система функций принадлежит любому функционально замкнутому классу, то и все суперпозиции этих функций принадлежат этому классу.
Докажем достаточность. Сначала, отождествляя переменные, упростим функции из 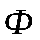
Действительно, возьмем из системы функций 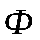
Пусть, например, 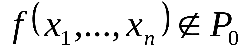
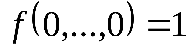
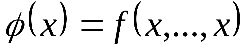
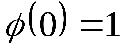
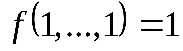
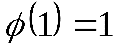
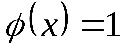
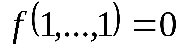
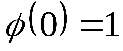
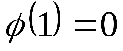
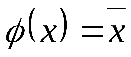
Таким образом, если функция не принадлежит классу 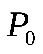

Пусть мы получим константы. Можно показать, что отрицание можно представить в виде суперпозиции. Это следует из теоремы 6 предыдущего параграфа.
При проверке, выполняются ли для некоторой системы функций 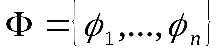
В клетках таблицы Поста ставится плюс или минус, в зависимости от того, входит функция, стоящая в данной строке, в класс, стоящий в данном столбце, или не входит. Для полноты системы функции необходимо и достаточно (в силу теоремы Поста), чтобы в каждом столбце присутствовал хотя бы один минус. Это будет означать, что для каждого из классов 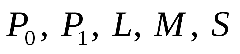
Данная система функций является полной, т. к. выполнены условия теоремы Поста. Кроме того, видно, что если убрать одну строку (например, последнюю), то получим неполную систему (знак плюс стоит в каждой строке в столбцах).
Определение 1: Функционально замкнутые классы, отличные от пустого класса и от совокупности всех функций алгебры логики, называются собственными функционально замкнутыми классами.
Определение 2: Собственный функционально замкнутый класс называется предполным, если он не содержится ни в каком функционально замкнутом классе, отличном от самого себя и от класса всех функций алгебры логики.
2. Ни один из классов не содержится в другом.
3. Действительно, если бы какой-либо класс содержался в другом, то в формулировке теоремы Поста этот класс можно было бы отбросить.
Рассмотрим таблицы Поста для следующих систем функций
Все рассмотренные здесь системы функций не полны, т.к. для каждой из них в таблице имеется столбец, состоящий сплошь из плюсов. Причем для каждой системы имеется ровно по одному такому столбцу, причем для разных систем эти столбцы разные. Отсюда следует, что в условии теоремы Поста нельзя отбросить ни одного из пяти классов. Действительно, для каждого из классов можно указать систему, содержащихся в нем функций (а значит, не полную), в которой для каждого из остальных четырех классов имеется функция, ему не принадлежащая.
Всякий собственный функционально замкнутый класс содержится в одном из классов.
Действительно, если некоторый функционально замкнутый класс не содержится ни в одном из пяти указанных классов, то для каждого из них в классе найдется функция, ему не принадлежащая. Но тогда по теореме Поста класс содержит все функции алгебры логики.
Теорема 2: Функционально замкнутые классы являются предполными и других предполных классов нет.
Доказательство: Из следствия 3 теоремы Поста следует, что других предполных классов нет, а из следствия 2 следует, что каждый из пяти перечисленных классов является предполным.
Замечание: Теорема Поста позволяет выяснить вопрос о том, является ли полная система базисом. Это удобно делать опять-таки с помощью таблиц Поста. Причем нетрудно видеть, что всякий базис не может содержать более пяти функций.
На самом деле имеет место более точный результат.
Теорема 3: Всякий базис полной системы функций не может содержать более четырех функций.
Доказательство: Заметим сначала, что если монотонная функция не сохраняет нуль, то она тождественно равна единице. Действительно, т. к. нулевой набор меньше любого другого, то из равенства на нем монотонной функции единице следует ее тождественное равенство единице (на остальных наборах значение функции не может быть меньше, чем на нулевом наборе). Аналогично, если монотонная функция не сохраняет единицу, то она тождественно равна нулю.
Возьмем теперь функцию, не сохраняющую нуль. В силу сделанного замечания, она или является немонотонной или является тождественной единице, т. е. несамодвойственной функцией. Итак, в полной системе обязательно найдется функция, не принадлежащая сразу двум предполным классам. Тогда к этой функции можно присоединить не более трех функций из рассматриваемой системы так, чтобы удовлетворялись условия теоремы Поста. Значит, в базисе не может быть более четырех функций. Что и требовалось доказать.
Замечание об общей теории функционально замкнутых классов.
Общая теория функционально замкнутых классов построена известным американским математиком Э. Постом (результат оформлен в виде монографии в 1941г.). Основным результатом этой работы является построение всех подалгебр (т.е. функционально замкнутых систем) алгебры логики.
Мы выяснили, что вопрос о полноте системы функций алгебры логики приводит к рассмотрению предполных функционально замкнутых классов. Оказывается, что целый ряд вопросов сводится к изучению других функционально замкнутых классов, не обязательно предполных. Можно ожидать, что число различных функционально замкнутых классов бесконечно и даже что их множество имеет мощность континуум. Действительно, классы естественно задавать какими-либо системами функций, их порождающими. Поскольку множество функции алгебры логики счётно, множество различных систем функций имеет мощность континуум. Конечно, различные системы функций часто порождают один и тот же класс. Но нет оснований заранее считать это отождествление настолько сильно, что число различных классов будет конечно или счётно. На самом деле оказывается, что множество классов счётно.

