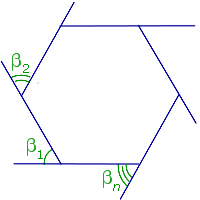
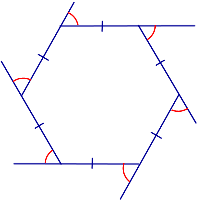
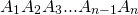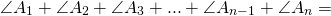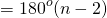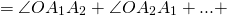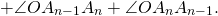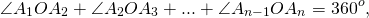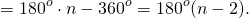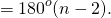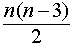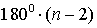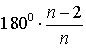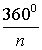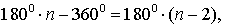Докажите что угол правильного n угольника равен n 2 n 180
Сумма углов многоугольника
(о сумме углов выпуклого многоугольника)
Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).
(n — количество сторон многоугольника).
Другой вариант формулировки этой теоремы:
Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

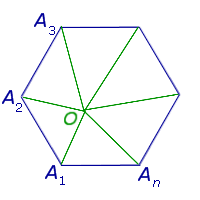
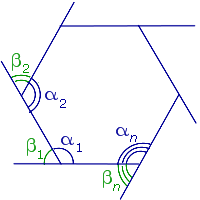
Обозначим внутри многоугольника произвольную точку O.
Соединим точку O с вершинами многоугольника.
Получили n треугольников.
Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.
Так как сумма углов при вершине O составляет 360º
то сумма углов многоугольника равна сумме углов n треугольников минус 360º.
Таким образом, искомая сумма углов n угольника равна

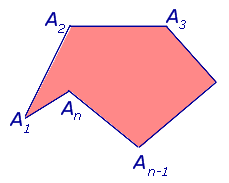
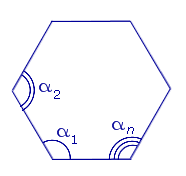
Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.
Сумма всех углов этих треугольников равна сумме углов многоугольника.
Сумма углов углов каждого из треугольников равна 180º.
Следовательно, сумма углов многоугольника
Что и требовалось доказать.
4 Comments
Нужно либо поменять название статьи, либо добавить в текст информацию о невыпуклых многоугольниках.
А так сайт оказался полезным, спасибо!
Ольга, спасибо. Подкорректирую в июне.
Очень хороший сайт! Давно им пользуюсь. Спасибо за Ваш труд!
Многоугольники
 Определение многоугольника Определение многоугольника |
 Диагонали n – угольника Диагонали n – угольника |
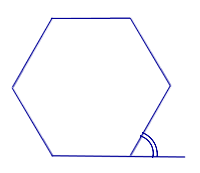
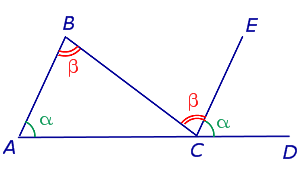
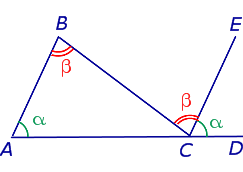
 Внешний угол многоугольника Внешний угол многоугольника |
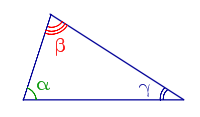
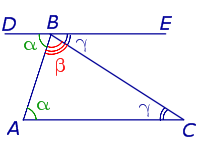
 Свойства углов треугольника Свойства углов треугольника |
 Свойства углов многоугольника Свойства углов многоугольника |
 Свойства углов правильного n – угольника Свойства углов правильного n – угольника |
 Доказательства теорем о свойствах углов многоугольника Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
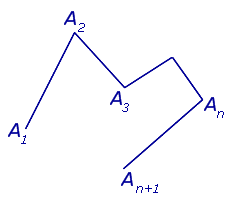
Рассмотрим n отрезков
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
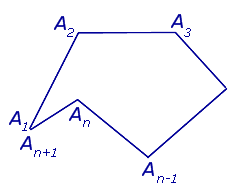
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
| Фигура | Рисунок | Описание | |||||||||||||||||
| Диагональ многоугольника | 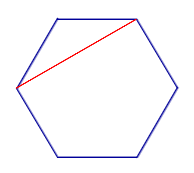 | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника | |||||||||||||||||
| Диагонали n – угольника, выходящие из одной вершины | 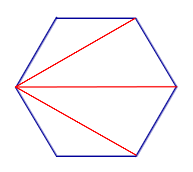 | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |||||||||||||||||
| Все диагонали n – угольника | 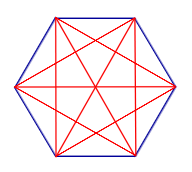 | ||||||||||||||||||
| Диагонали n – угольника, выходящие из одной вершины | |||||||||||||||||||
 Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |||||||||||||||||||
| Все диагонали n – угольника | |||||||||||||||||||
 Число диагоналей n – угольника равно Внешний угол многоугольникаСвойства углов треугольника
|