Единица измерения дбм что это
О насущном вопросе: как перевести из дБм в дБ? (часть 2)
На многих форумах люди задают вопрос: как перевести из дБ в дБм?
Как было показано выше, преимущество логарифмической шкалы очевидно в случае, когда мы исследуем во сколько раз значение одной величины больше или меньше другой.
Например, потери на элементе ВОЛС (в сплиттере, в ОВ или механическом соединителе) определяются соотношением:
где P1 и P2 – мощности сигнала соответственно на входе и выходе элемента, выраженные в Вт, мВт (mВт, милливатт) или мкВт (μВт, микроватт).
Помимо дБ, существует еще одна похожая логарифмическая единица измерения – дБм. В отличие от дБ, которые характеризуют потери (во сколько раз уменьшается мощность оптического сигнала) или усиление (во сколько раз увеличивается мощность оптического сигнала), дБм показывают уровень мощности сигнала, относительно опорной мощности равной 1 мВт.
Перевод мощности сигнала из мВт в логарифмическую шкалу – дБм, производится измерителем оптического излучения по формуле
где P0=1 мВт – абсолютный нулевой уровень, рекомендованный МСЭ-Т (международным союзом электросвязи, сектором стандартизации). Буква «м», добавленная после дБ, означает, что в качестве опорного уровня мощности взят 1 мВт. Если качестве опорного уровня мощности взять 1 мкВт, то обозначение будет иметь вид дБмк. В англоязычной литературе часто dBm обозначают dBmW, (переводя на рус. – дБмВт), акцентируя внимание на то, что дБ взят по мощности, а не по напряжению или току. Для сокращения записи обычно Вт опускают, и остается просто дБм.
Может возникнуть вопрос, зачем мощность сигнала переводить в дБм? Ответ очевиден – чтобы можно было при расчетах оперировать с дБ и в результате возникающих в линии связи (проводной или беспроводной) потерь и усилений сигнала вычислить его уровень на входе приемника.
Хорошо, почему тогда в качестве опорного уровня принят 1 мВт, не проще было бы взять P0=1 Вт и уровень сигнала отображать также в дБ? Согласно ОСТ 45.159-2000, децибел – это логарифмическая единица уровней, затуханий и усилений. Поэтому уровень сигнала также можно выражать в дБ, только в этом случае, по-видимому, чтобы не путать уровень сигнала с потерями используют обозначение дБВт (англ. dBW)
Обратное преобразование из дБВт в Вт осуществляется по следующей формуле:
Почему в качестве опорного уровня принят 1 мВт? Честно говоря, ответ на этот вопрос нигде не встречается. На наш взгляд это значение используется в силу следующих обстоятельств.
В связи с этим, если бы мы для отображения уровня сигнала использовали дБВт, то нам пришлось бы работать с отрицательными величинами: 1 мВт соответствует минус 30 дБВт, 50 мВт соответствует минус 13 дБВт. Очевидно, это вызывает некоторую путаницу – большая мощность соответствует меньшему уровню сигнала. Таким образом, выражение уровня мощности в дБм в системах телекоммуникаций в большинстве случаев является более удобным, нежели дБВт.
Возможно также, что выбор опорной мощности в 1 мВт появился в результате следующих обстоятельств. Исторически сложилось в качестве действующего значения опорного напряжения в канале передачи брать 0.775 В (из ранних телефонных стандартов), а в качестве нагрузки 600 Ом (сопротивление катушек приемного электромагнита у аппарата Морзе). В этом случае рассеиваемая мощность на нагрузке будет составлять 1 мВт.
Познавательные факты
Довольно часто, наравне с децибелами применяются неперы. Непер – логарифмическая величина (натуральный логарифм безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную). Своё название данная единица получила в честь математика, «изобретателя логарифмов» Джона Непера.
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
При некотором навыке операции с децибелами вполне реально выполнять в уме. Для этого полезно помнить следующие взаимосвязи:
1 дБ – в 1.25 раза,
3 дБ – в 2 раза,
10 дБ – в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
6 дБ = 3 дБ + 3 дБ – в 2·2 = в 4 раза,
12 дБ = 4 · (3 дБ) – в 24 = в 16 раз
13 дБ = 10 дБ + 3 дБ – в 10·2 = в 20 раз,
20 дБ = 10 дБ + 10 дБ – в 10·10 = в 100 раз,
О децибелах для радиоинженеров
Узнайте о децибелах и их вариациях в контексте радиочастотного проектирования и тестирования.
Радиотехника, как и все научные дисциплины и подразделы, включает в себя довольно много специализированной терминологии. Одним из наиболее важных слов, которые вам понадобятся при работе в мире радиочастот, является «дБ» (и некоторые его варианты). Если вы глубоко закрепились в проектировании радиочастотных систем, то можете обнаружить, что слово «дБ» становится вам таким же знакомым, как и ваше собственное имя.
Как вы, наверное, знаете, дБ означает децибел. Это логарифмическая единица, которая обеспечивает удобный способ работы с отношениями, такими как отношение между амплитудами входного и выходного сигналов.
Мы не будем описывать общую информацию о децибелах, потому что она уже доступна на этой странице учебника «Основы электроники и схемотехники». Вместо этого мы сосредоточимся на практических аспектах децибелов в конкретном контексте радиочастотных систем.
Относительный, не абсолютный
Легко забыть, что дБ является относительной единицей. Вы не можете сказать: «Выходная мощность составляет 10 дБ».
Напряжение является абсолютной величиной, потому что мы всегда говорим о разности потенциалов между двумя точками; обычно мы имеем в виду потенциал одного узла относительно узла земли 0 В. Ток также является абсолютной величиной, поскольку единица измерения (ампер) включает в себя определенное количество заряда в течение определенного количества времени. Децибел, напротив, это единица измерения, которая включает в себя логарифм отношения между двумя числами. Ярким примером является коэффициент усиления усилителя: если мощность входного сигнала равна 1 Вт, а мощность выходного сигнала равна 5 Вт, мы имеем коэффициент 5:
\[10 \log_ <10>\left( < P_<вых>\over P_ <вх>> \right) = 10 \log_ <10>(5) \approx 7 дБ\]
Таким образом, этот усилитель обеспечивает усиление по мощности 7 дБ, то есть соотношение между мощностью выходного сигнала и мощностью входного сигнала может быть выражено как 7 дБ.
Почему дБ?
Конечно, можно было бы проектировать и тестировать радиочастотные системы без использования дБ, но на практике дБ используются везде. Одно из преимуществ заключается в том, что шкала дБ позволяет выражать очень большие отношения без использования очень больших чисел: усиление по мощности в 1 000 000 раз составляет всего 60 дБ. Кроме того, при использовании дБ легко вычисляется общий коэффициент усиления или потерь в цепи прохождения сигнала, поскольку отдельные значения в дБ просто складываются (тогда как, если бы мы работали с обычными отношениями, нам потребовалось бы умножение).
Еще одно преимущество – это то, что мы знаем из нашего опыта работы с фильтрами. Радиочастотные системы вращаются вокруг частот и различных способов генерации, управления или воздействия на эти частоты с помощью компонентов и паразитных элементов схемы. Шкала в дБ в подобном контексте удобна, потому что графики частотных характеристик интуитивно понятны и визуально информативны, когда ось частот использует логарифмический масштаб, а ось амплитуды использует шкалу в дБ.
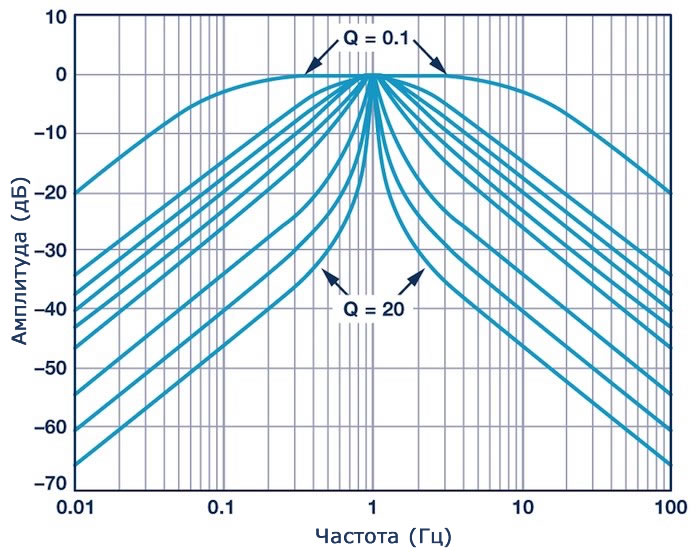
Когда дБ абсолютны?
Мы установили, что дБ является отношением и, следовательно, не может описывать абсолютные значения мощности и амплитуды сигнала. Однако было бы неудобно постоянно переключаться между значениями в дБ и не в дБ, и, возможно, именно поэтому радиоинженеры ввели единицу измерения дБм (dBm).
Мы можем избежать проблемы «только отношение», просто создав новую единицу измерения, которая всегда будет содержать опорное значение. В случае дБм опорное значение равно 1 мВт. Таким образом, если у нас есть сигнал 5 мВт, и мы хотим оставаться в области дБ, мы можем выразить мощность этого сигнала как 7дБм:
\[10 \log_ <10>\left( < 5 мВт \over 1 мВт >\right) = 10 \log_ <10>(5) \approx 7 дБм\]
Вы определенно хотите ознакомиться с концепцией дБм. Это стандартная единица, используемая в реальной разработке радиочастотных систем, и она очень удобна, когда вы, например, вычисляете энергетический баланс линии связи, поскольку усиления и потери, выраженные в дБ, могут просто складываться и вычитаться из выходной мощности, выраженной в дБм.
Существует также единица дБВт (dBW); в качестве опорного значения она использует 1 Вт вместо 1 мВт. В настоящее время большинство радиоинженеров работает с относительно маломощными системами, и это, вероятно, объясняет, почему дБм встречается чаще.
Больше вариаций дБ
Две других единицы измерения, основанных на дБ, – это дБн (dBc) и дБи (dBi).
Вместо фиксированного значения, такого как 1 мВт, дБн (dBc) использует в качестве опорного сигнала уровень несущей сигнала. Например, фазовый шум (смотрите второй раздел данной главы) выражается в единицах дБн/Гц (dBc/Hz); первая часть этой единицы измерения указывает, что мощность фазового шума на определенной частоте измеряется относительно мощности несущей (в этом случае «несущая» относится к мощности сигнала на номинальной частоте).
Идеализированная точечная антенна принимает определенное количество энергии от схемы передатчика и равномерно излучает ее во всех направлениях. Считается, что эти «изотропные» антенны имеют нулевой коэффициент усиления и нулевые потери.
Однако, другие антенны могут быть сконструированы таким образом, чтобы концентрировать излучаемую энергию в определенных направлениях, и в этом смысле антенна может иметь «усиление». Антенна на самом деле не добавляет мощности к сигналу, но эффективно увеличивает переданную мощность путем концентрации электромагнитного излучения в соответствии с направлением системы связи (очевидно, что более практично, когда разработчик антенны знает пространственную взаимосвязь между передатчиком и приемником).
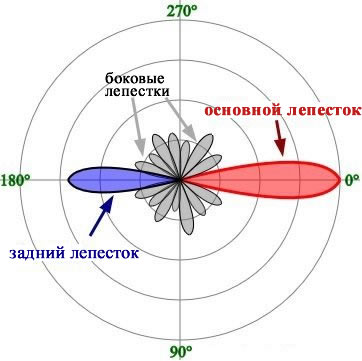
Единица измерения дБи (dBi) позволяет производителям антенн указывать «коэффициент усиления», который использует популярную шкалу дБ. Как всегда, когда мы работаем с дБ, нам необходимо отношение, а в случае с дБи (dBi) коэффициент усиления антенны выражается через опорное усиление изотропной антенны.
Некоторые антенны (например, те, которые сопровождаются параболическим зеркалом, «тарелкой») имеют значительный коэффициент усиления, и поэтому они могут внести нетривиальный вклад в расстояние и производительность радиочастотной системы.
Как определять и различать дБ, дБм и дБи?
«Что такое дБ, дБи, дБм и дБВт в теории усиления антенны? В чем разница между дБ, дБи, дБм и дБВт? Следующее содержание является основной теорией об антенне, это может помочь вам ее ваше признание технологии RF. —— FMUSER «
Если вам это нравится, поделитесь!
Контент (Нажмите, чтобы увидеть! )
5 C широко используется Децибелы (Нажмите, чтобы посетить)

1. Что такое прибыль?
Когда мощность, выходящая из оборудования, превышает мощность, поступающую в оборудование, считается, что мощность увеличивается. Когда вы добавляете усилитель сигнала в свой дом или офис, устройство принимает существующий сигнал и усиливает или увеличивает мощность, что делает возможным более сильный интернет-сигнал или соединение. Измерение коэффициента усиления позволяет выбрать идеальное устройство для ваших нужд. Величина усиления измеряется в децибелах.
2. Что такое дБ ( Децибел ) ?
1) Определение децибел
● По амплитуде
Амплитуда, представленная в шкале дБ (децибел), используется для измерения и индикации ее силы или давления. Проще говоря, если он будет с большей амплитудой, звук может быть как можно громче. Для этого звук называется давлением 0.0002 микробар, что соответствует стандарту для порога слышимости.
● С точки зрения частоты
Частота, которая указывается в Гц (Герцах), используется для измерения и указания определенного количества звуковых колебаний в секунду.
Согласно своим характеристикам, децибелы или дБ широко используются в научных измерительных приложениях, таких как измерения в электротехнике (электроника, определение коэффициентов усиления, потери компонентов, например, аттенюаторы, фидеры, смесители и т. Д.), Измерения звука (акустика, коэффициент шума и т. Д.) отношение сигнал / шум и т. д.), теория управления (графики Боде и т. д.), сигналы и связь и т. д.
2) Когда и как обнаруживаются децибелы?
Термин бел, появившийся при измерении потерь передачи и мощности в телефонии в начале 20 века (1928) в системе Белла в Соединенных Штатах, на самом деле происходит от логарифмической единицы измерения, называемой бел, которая создается Bell Telephone Laboratories и названа в честь ее основателя Александра Грэма Белла.
По сравнению с редко используемым белом, децибел является предлагаемой рабочей единицей, потому что разница в громкости в один децибел между двумя звуками является наименьшей разницей, обнаруживаемой человеческим слухом, а децибел составляет лишь одну десятую бела, т.е. используется для самых разных измерений в науке и технике (как упоминалось выше).
Также есть дБ относительно уровней НАПРЯЖЕНИЯ, но я не буду вдаваться в них, поскольку в наших обсуждениях мы в основном озабочены уровнями МОЩНОСТИ. 3 дБ в два (или половину) раза больше, 6 дБ в четыре раза, 10 дБ в десять раз и так далее. Формула для расчета усиления или потерь в дБ: 10log P1 / P2. Он используется для указания усиления или потери одного устройства (P1) В ОТНОШЕНИИ другого (P2). Таким образом, я могу сказать, что усилитель имеет усиление 30 дБ, или у меня общие потери в фиде 6 дБ. Я НЕ МОГУ сказать, мой усилитель выдает 30 дБ, или у меня антенна на 24 дБ, так как вы должны указать, на что вы ссылаетесь, и именно здесь появляется нижний индекс. ДБ сам по себе не является абсолютным числом, но соотношение.
● Для усилителей
● Для антенн
Это может быть антенна 26.41 дБи (24 дБд) или 21.59 дБи (также 24 дБд!), В зависимости от того, какой у меня был исходный эталон. Разница составляет 4.81 дБ, значительное количество. Большинство производителей антенн отказались играть в эту игру, но референция будет отличаться в разных областях.
Коммерческие антенны, как правило, оценивается в дБи, как людей, покупающих их понимаю, и радиолюбителей антенны, как правило, дБд, как ветчины очень хорошо знакомы с диполей.
3. Что такое децибел-милливатт (дБм или дБмВт)?
(Децибелы при 1 милливатте) Измерение мощности с использованием одного милливатта в качестве контрольной точки (0 дБмВт). Например, сигнал мощностью 1 милливатта (100 микроватт) означает потерю 10 дБмВт. Радиостанция, передающая мощность 50,000 XNUMX Вт, может ослабнуть до пары милливатт к тому времени, когда она будет принята радиоприемником.
Советы: как преобразовать дБм в ватты?
Для систем с низким энергопотреблением, таких как те, которые используются в мобильной связи, шкала дБм (децибел-милливатт) является удобным эталонным уровнем мощности, в котором мощность относится к уровню 1 мВт:
P (дБм) = 10log (P (мВт) / 1 мВт)
Таким образом, если антенна имеет усиление 5 дБи в определенном направлении, это означает, что по сравнению с изотропной антенной (которая будет иметь усиление в этом направлении 0 дБ), эта антенна имеет усиление 5 дБ.
Вы даже можете рассматривать дБи как измерение, которое сравнивает усиление антенны с изотропным излучателем (теоретическая антенна, которая излучает энергию равномерно по сферической диаграмме).
Для вас важно знать, что усилитель сигнала поставляется с антенной со значением дБи.
5. Что такое децибел-ватт (дБВт) ?
Децибел ватт (дБВт) означает децибел относительно 1 ватта, это единица измерения силы сигнала, выраженная в децибелах относительно одного ватта. Мощность в дБВт равна десятикратному логарифму мощности в ваттах по основанию 10. Это очень полезно, так как может выражать большой диапазон значений в коротком диапазоне чисел.
Для мощных систем, таких как те, которые используются в спутниковой связи, обычно используется шкала дБВт (децибел-ватт), в которой мощность относится к 1 Вт:
P (дБВт) = 10log (P (Вт) / 1 Вт)
В чем разница разница между дБ и дБм?
● Децибел (дБ) и дБ относительно милливатта (дБм) представляют собой две разные, но взаимосвязанные концепции.
единица дБм обозначает абсолютный уровень мощности, измеренный в децибел и отнесено к 1 милливатт (мВт). Чтобы преобразовать абсолютную мощность «P» (в ваттах) в дБм, используйте формулу dBm = 10 * log (P / 1 мВт). Это уравнение выглядит почти так же, как и для дБ. Тем не менее, теперь уровень мощности «P» был привязан к 1 мВт. Оказывается, в практическом мире радиосвязи 1 мВт является удобной точкой отсчета для измерения мощности.
Используйте дБ, когда выраж эссинга соотношение между двумя значениями мощности. Используйте дБм при выражении абсолютного значения мощности.
Во многих описаний о FM продуктов, мы продолжаем видеть, как люди используют термины «БД», «дБм», и «дБи» как синонимы, когда они на самом деле означает совершенно разные вещи. Итак, вот небольшой фон от правильного использования терминов.
В чем разница между дБ и дБи?
● Представьте себе антенну, которая излучает энергию одинаково во всех направлениях, как наше Солнце. На научном жаргоне это называется «изотропным излучателем», потому что он не предпочитает излучение в любом направлении… другими словами, у него нет «направленности».
● Этот тип изотропной антенны называется «без усиления». «Нет усиления» может быть выражено в линейных терминах, таких как x1 (раз 1). Это просто означает, что все направления имеют одинаковую энергию излучения и все равны средней энергии излучения. Инженеры-антенны любят логарифмические термины, и мы говорим, что эта ситуация без усиления равна 0 дБи (произносится как «ноль ди глаз»). Представьте себе гигантское зеркало звездного размера рядом с нашим солнцем. Представьте, как это изменило бы это распределение энергии и дало бы солнечную направленность. Работы С Нами В таком воображаемом зеркале одна половина нашей солнечной системы будет темной (за зеркалом).
● Другая половина будет в два раза ярче (если смотреть на прямое солнце и его отражение). Зеркала или линзы имеют вид усиления энергии в некоторых предпочтительных направлениях путем кражи и перенаправления ее в неблагоприятных направлениях. Антенны делают то же самое.
● Зеркала не создают свет, они только отклоняют, направляют или концентрируют его в каком-то направлении. Антенны не создают радиоэнергию, они только отклоняют, направляют или концентрируют ее в каком-то направлении. Эта характеристика направленности называется усилением. Пожалуйста, помните, никакой новой энергии не создается, она просто перенаправляется или задается направленностью (направленностью). Величина усиления в предпочтительном направлении определяется количественно как усиление. Таким образом, зеркало может перенаправить половину энергии солнца (или свечи) и сделать его в два раза ярче (например, две свечи). Говорят иметь е увеличение в 2 раза (умноженное на два) или удвоение.
-10 дБи
Одна десятая, 1/10 или «10%» (убыток, а не прибыль)
-6 дБи
Одна четверть, 1/4 или «25%» (убыток, а не прибыль)
-3 дБи
Половина, 1/2 или «50%» (убыток, а не прибыль)
0 дБи
Без прироста, «то же самое», 100% (без прироста, без потерь)
+1 дБи
На 12% больше, раз 1.12, или 112%
+2 дБи
На 58% больше, раз 1.58, или 158%
+3 дБи
На 100% выше, умноженное на 2, «вдвое» или на 200%
+6 дБи
300% выше, раз 4
+9 дБи
Времена 8 (% масштаб не полезен для больших кратных)
+10 дБи
Времена 10 (% масштаб не полезен для больших кратных)
+13 дБи
Времена 20 (% масштаб не полезен для больших кратных)
+20 дБи
Времена 100 (% масштаб не полезен для больших кратных)
Вас также могут заинтересовать:
Если вам это нравится, поделитесь!
О насущном вопросе: как перевести из дБм в дБ? (часть 1)
Наверное, каждый связист хоть раз в жизни встречался с такой единицей измерения как «дБм» (произносится как набор отдельных букв алфавита в соответствии с транскрипцией [дэ]-[бэ]-[эм]). Например, специалисты в области волоконно-оптических линий связи (ВОЛС) с данной единицей измерения сталкиваются при выборе источника излучения и фотоприемника – в дБм указан максимально возможный уровень сигнала на выходе источника и минимально допустимый уровень сигнала на входе приемника. Далее эта информация используется при проектировании линии связи, когда производится расчет энергетического бюджета системы и строится диаграмма уровней сигнала. Стоит отметить, что расчет энергетического бюджета системы является одной из самых главных частей проекта ВОЛС и неважно, проектируете вы абонентскую сеть по технологии PON или транспортную сеть по технологии DWDM. Поэтому чтобы произвести этот расчет правильно необходимо полностью понимать смысл всех производимых операций, в том числе конечно и физический смысл единиц измерения рассчитываемых величин. Кроме того, с дБм приходится иметь дело при выполнении входного контроля волоконно-оптического кабеля с помощью тестера при измерении общих потерь в оптическом волокне (ОВ) – на экране измерителя оптического излучения вы будете видеть значение уровня сигнала в дБм.
Таким образом, единица измерения дБм фигурирует довольно часто как при описании характеристик телекоммуникационного оборудования, так и при расчетах и измерениях параметров сети. Однако мало кто понимает смысл данной величины, ее отличие и совместимость с привычными всем децибелами (дБ). На различных форумах часто задают вопросы: как осуществляется перевод величины из дБ в дБм и обратно? Прочитав данную статью, вы поймете, что данный вопрос на самом деле является бессмысленным.
Целью статьи является рассмотрение и разъяснение понятия «дБм», его отличия от единицы измерения «дБ», рассмотрение практических примеров использования данных величин с пояснением используемых формул и последующих рекомендаций по их применению.
Однако прежде чем перейти к рассуждению о единице дБм необходимо, чтобы читатель хорошо понимал смысл дБ. Поэтому сначала рассмотрим истоки появления такой величины как дБ и ее преимущества в сравнении с абсолютными величинами.
Изложенный материал является базовым, однако как показывает практика понимаемый далеко не всеми. Может быть даже тот, кто хорошо разбирается в данном вопросе, откроет для себя какие-то новые факты или примеры.
Если мощность сигнала измеряется в ватах, зачем тогда нужны децибелы?
Всем известно, что в 1876 г. Александр Грэхем Белл изобрел телефон (хотя 11 июня 2002 года Конгресс США в резолюции № 269 признал, что, первенство в этом изобретении принадлежит итальянскому ученому Антонио Меуччи (итал. Antonio Meucci, 13 апреля 1808 – 18 октября 1889), который подал заявку на соответствующий патент в 1871 г.). В связи с этим, по-видимому с целью оценки качества телефонной связи за единицу измерения уровня интенсивности звука приняли 1 Б (Белл).
Согласно определению из ГОСТ 8.4172002: Белл – логарифм безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную: уровень звукового давления; усиление, ослабление и т.п. То есть 1 Белл соответствует такой интенсивности звука, которая превышает пороговую интенсивность в 10 раз:
где A – уровень интенсивности звука; Y– интенсивность звука (отношение падающей на поверхности звуковой мощности к площади этой поверхности, измеряется в [Вт/м2]); Y0 – пороговая интенсивность. Для тех, кто плохо разбирается в математике, поясним, что обозначение lg (x) по общепринятым правилам соответствует десятичному логарифму x (или, другими словами, логарифм x по основанию 10), lg(x)=log10(x).. Пороговая интенсивность Y0 – это минимальная интенсивность звука, воспринимаемая человеком.
Силу звука издавна измеряют в дБ, например, шелест листьев производит шум силой 30 дБ, оркестр – 80 децибел, а реактивный двигатель – от 120 до 140 децибел. Водопад Ниагара производит шум, сравнимый с шумом фабричного цеха (90-100 децибел). В Книге Рекордов Гиннеса зафиксирован случай: 14-летняя шотландская школьница, перекричала взлетающий самолет «Боинг» [3].
Здесь возникает разумный вопрос: зачем перешли от абсолютных единиц измерения интенсивности звука Вт/м2 к относительным – децибелам?
Диапазон величин интенсивности звука, которые способен слышать человек является довольно широким. Человек способен слышать звуки, различающиеся по уровню в 100000 раз и если отобразить этот диапазон значений на одной координатной оси, масштаб окажется весьма неудачным. То есть пользоваться линейной зависимостью для выявления того, во сколько раз одна величина больше другой довольно неудобно.
Кроме того, чувствительность слуха не линейна и изменяется по логарифмическому закону. Допустим, на выходе усилителя имеется звуковой сигнал с напряжением 1 В. Для увеличения громкости в 1.1 раза надо увеличить напряжение всего на 0.1 В. Однако если на выходе усилителя было 100 В, то для увеличения громкости в 1.1 раза нужно добавить 10 В (данные значения конечно абстрактные). В обоих случаях человеку будет казаться, что приращение громкости было одинаковым.
Несмотря на то, что децибел первоначально использовался для выражения уровня звукового сигнала, в настоящее время в виду его полезных свойств он широко применяется в самых различных областях. Особенно в случае измерения величин, меняющихся в широком диапазоне: в радиотехнике, например при построении диаграммы направленности антенны, в системах передачи информации, в оптике, в автомобильной акустике и др.
Рассмотрим полезные свойства децибелов, рассматривая примеры из области связи. На рис. 1 изображена амплитудная характеристика оптического фильтра, используемого в WDM-системах спектрального уплотнения, реализованного на 7 мм волоконной Брэгговской решетке. Ниже на рис. 2 изображена передаточная функция электрического цифрового фильтра, реализующего сглаживание сигнала по 15-ти точечной формуле Спенсера. Данный фильтр используется в цифровой обработке сигналов для подавления шума.
б)
Рис. 1 Амплитудная характеристика оптического фильтра, используемого в WDM-системах, реализованного на 7 мм волоконной Брэгговской решетке: а) в логарифмическом масштабе; б) в линейном масштабе.
б)
Рис. 2 Передаточная функция цифрового фильтра: а) в логарифмическом масштабе; б) в линейном масштабе.
Как видно из рис. 1,2 при использовании логарифмической шкалы информативность амплитудной характеристики оптического фильтра и передаточной функции цифрового фильтра значительно повышается. Логарифмическая шкала как бы придает больший масштаб маленьким единицам и меньший масштаб большим.
Данное свойство исходит из характера изменения логарифмической функции. На рис. 3 приведен график функции y=lg(x). Как видно из рисунка, приращение по x в области относительно малых величин дает некоторое приращение dy. Например, если в качестве dx взять изменение отношения мощностей сигнала (в ватах) с 10 до 20 раз, то приращение dy – значение в дБ, поменяется с 10 до 13, т.е. на 3 дБ. Чтобы получить такое же приращение dy в области относительно больших величин, приращение по x нужно брать уже в разы больше. Та же разность в 3 дБ, будет соответствовать изменению отношения мощностей сигнала с 20000 до 39811 раз.
Рис. 3 График логарифмической функции
Например, если мы скажем, что при распространении сигнала в ОВ G.652 CORNING Inc. SMF-28e+ длиной 1 км на длине волны 1550 нм его мощность уменьшилась с 10 мВт до 9.506 мВт, а в ОВ G.655 LEAF на той же длине волны мощность уменьшилась с 4.2 мВт до 3.99 мВт, в этом случае сложно сказать одинаковое затухание вносят данные ОВ или нет. Если мы скажем, что на каждом километре оптических волокон G.652 и G.655, мощность сигнала уменьшается в 1.052 раз, то информация приобретает более интересный характер. В этом случае можно уже сказать, что они имеют равное затухание. Однако данный критерий все еще неидеален. Например, если мы захотим узнать, во сколько уменьшается мощность сигнала в этих волокнах длиной 6 км, потребуется 1.052 умножить само на себя 6 раз. Думаю, вряд ли кто-нибудь с ходу сможет сказать результат. Если же данное отношение выразить в логарифмических единицах, то можно сказать, что на 1 км уровень мощности сигнала уменьшается на 0.22 дБ, на 6 км – на 6*0.22=1.32 дБ. Как видно, с использованием логарифмических единиц расчеты стали значительно проще.
Таким образом, децибел является естественной единицей измерения многих физических и биологических процессов (в том числе чувствительность слуха), изменяющихся по логарифмическому закону. Логарифмическая шкала обеспечивает удобство отображения и анализа величины, изменяющейся в очень широком диапазоне. Расчеты с использованием логарифмических единиц становятся значительно проще.














