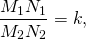какие фигуры в пространстве называются подобными

Подобие фигур

Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.

Содержание:

Понятие подобия фигур

В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.

Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.

Для обозначения подобия фигур употребляется знак . На рисунке 2.434 изображены подобные фигуры . Запись читается: фигура подобна фигуре

Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.

Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.

Определение. Масштаб — это коэффициент подобия соответствующих фигур.

Подобие треугольников

На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны: Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.

Подобие треугольников записывается так: Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников будет число 2. Если же взять отношения , коэффициент подобия будет равен .

Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.

Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.

Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.

Для выявления подобия треугольников существуют признаки подобия треугольников.

Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Следствия из этой теоремы.

1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.

Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Подобие многоугольников

Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.

Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).

Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).

Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Презентация по геометрии «подобие пространственных фигур»

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Презентация по геометрии на тему: «Подобие пространственных фигур»

Преобразование подобия Если при преобразовании фигуры F в фигуру F` расстояние между точками изменяется в одно и тоже число раз, то такое преобразование называется преобразованием подобия. Т.е. произвольные точки AB фигуры F переходят в точки A`B` фигуры F`, так что A`B` =k*AB. Число k – это коэффициент подобия.

Свойства преобразования подобия Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки. Преобразование подобия сохраняет углы между полупрямыми. Точки, лежащие на прямой при преобразовании подобия переходят в точки, лежащие на прямой, а также сохраняется порядок их взаиморасположения.

Подобные фигуры Фигуры, полученные при преобразовании подобия, называются подобными фигурами

Свойства подобных фигур Если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигура F1 подобна фигуре F3. У подобных фигур соответствующие углы равны. Соответствующие отрезки у подобных фигур пропорциональны, т.е. изменены в одно и то число раз.

Гомотетия с центром O и коэффициентом k — это преобразование, в котором каждая точка P отображается такой точкой P1,что OP1=k⋅OP,гдеk≠0

Чтобы гомотетия была определена, должен быть задан центр гомотетии и коэффициент. Это можно записать так: гомотетия (O;k).

На рисунке из фигуры F можно получить фигуру F1 гомотетией (O;2).

Если фигуры находятся на противоположных направлениях от центра гомотетии, то коэффициент отрицательный. На рисунке из фигуры F можно получить фигуру F1 гомотетией (O;−2).

Центр гомотетии может находиться и внутри фигуры. Серый треугольник из зелёного треугольника ABC получен гомотетией (O; 1/2).

Гомотетия (O;−1) — это центральная симметрия или поворот на 180 градусов, в данном случае фигуры одинаковые.

Формулы гомотетии с центром в начале координат и коэффициентом k Х’=kx Y’=ky Z’=kz

Cвойства гомотетии 1)При гомотетии величина плоского и двухгранного угла сохраняется. 2)При гомотетии с коэффициентом k расстояние между точками изменяется в lkl раз 3)Отношение площадей гомотетических фигур равно квадрату коэффициента гомотетии. 4)Отношение объемов гомотетических фигур равно модулю куба коэффициента гомотетии. 5)Гомотетия с положительным коэффициентом не меняет ориентации пространства, а с отрицательным меняет.

6) Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя, при k=1)

Проверь себя: 1. Подобные фигуры это фигуры, полученные при преобразовании подобия. 2. Если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигура F1 не подобна фигуре F3. Преобразование подобия переводит прямые в полупрямые, а отрезки в отрезки. При гомотетии величина плоского угла остается та же, а величина двухгранного угла меняется. Отношение объемов гомотетических фигур равно модулю квадрата коэффициента гомотетии

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДБ-070117

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Прослушивание музыки снижает усталость мозга

Время чтения: 1 минута

В Ульяновской области продлили школьные каникулы

Время чтения: 1 минута

Технопарк универсальных педагогических компетенций откроют в Чечне

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

Мишустин поручил проводить международную олимпиаду по философии

Время чтения: 0 минут

Кабмин утвердил список вузов, в которых можно получить второе высшее образование бесплатно

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Подобие фигур

Подобие — это понятие, характеризующее наличие одинаковой, не зависящей от размеров, формы у геометрических фигур.

Подобные фигуры — это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.

Например, то, что фигуры F1 м F2 подобны означает, что для любых двух точек M1 и N1 фигуры F1 и сопоставленных им точек M2 и N2 фигуры F2 выполняется соответствие

где k — одно и тоже число для всех точек (k>0).

Число k называется коэффициентом подобия.

Преобразование фигуры F1 в фигуру F2, при котором расстояния между точками изменяется в одно и то же число раз, называется преобразованием подобия.

При k=1 преобразование подобия является движением.

Свойства преобразования подобия

1) Преобразование подобия переводит прямые в прямые, полупрямые — в полупрямые,отрезки — в отрезки.

2) Преобразование подобия сохраняет углы между полупрямыми.

Свойства подобных фигур

1) Если фигура F1 подобна фигуре F2, а фигура F2 — фигуре F3, то фигуры F1 и F3 подобны.

2) У подобных фигур соответствующие углы равны, а соответствующие стороны пропорциональны.

Подобие фигур в геометрии чаще всего связано с подобием треугольников.

Источник

Подобные фигуры

Содержание

Примеры

Связанные определения

Свойства

Обобщения

Аналогично определяется подобие (с сохранением указанных выше свойств) в 3-мерном евклидовом пространстве, а также в n-мерном евклидовом и псевдоевклидовом пространствах.

См. также

Полезное

Смотреть что такое «Подобные фигуры» в других словарях:

ПОДОБНЫЕ ФИГУРЫ — фигуры, у которых соответственные линейные элементы пропорциональны, а углы между ними равны, т. е. при одинаковой форме имеют разные размеры … Большая политехническая энциклопедия

Гомотетические фигуры — две гомологические фигуры называются Г., если расстояния соответствующих точек до центра пропорциональны. Отсюда видно, что Г. фигуры суть фигуры подобные и подобно расположенные, или же подобные и обратно расположенные. Центр гомологии в этом… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Пифагора теорема — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 Формулировки 2 Доказательства … Википедия

Щитодержатель — Щит Тинктуры Щитодержатель Щитодержатель (девиз) … Википедия

Шила-на-гиг — Известная Шила на гиг из церкви в Килпеке, Англия Шила на гиг (англ. Sheela na Gig) скульптурные изображения обнажённых женщин, обычно с увеличенной в … Википедия

ПОНЯТИЕ — общее имя с относительно ясным содержанием и сравнительно четко очерченным объемом. П. являются, напр., «химический элемент», «закон», «сила тяготения», «астрономия», «поэзия» и т.п. Отчетливой границы между теми именами, которые можно назвать П … Философская энциклопедия

Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

Планиметрия. Страница 9

1.Преобразование подобия и его свойства

Преобразованием подобия называется преобразование фигуры G в фигуру G’, у которой расстояние между точками изменяется в одно и тоже число раз. Т.е. ОA’ = k OA. Это означает, что для любых двух точек геометрической фигуры выполняется равенство A’B’ = k AB. (Рис.1) Число k называется коэффициентом подобия.

Если взять произвольную точку, например точку О. И отложить отрезок OB’ = k OB, то такое преобразование фигуры G в фигуру G’ называется гомотетией. А число k называется коэффициентом гомотетии. Таким образом, гомотетия есть преобразование подобия.

Свойства преобразования подобия

Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки и при этом углы между прямыми сохраняются.

6.Пример 1

Докажите, что фигура подобная окружности, есть окружность.

Доказательство:

Зададим на плоскости систему координат с осями Оx и Oy таким образом, чтобы центр первой окружности F совпал с началом координат. Параллельным переносом переместим вторую окружность F’ так, чтобы ее центр также совпал с началом координат. На окружности F возьмем две произвольные точки А и В. И проведем между ними хорду. Также проведем к этим точкам радиусы ОА и ОВ, которые продлим до окружности F’, т.е. ОA’ и OB’. Оси Оx и Оy повернем так, чтобы ось Oy пересекала хорду под прямым углом (Рис.7). Тогда k OA = OA’.

Теперь рассмотрим треугольник ОАС.

Рис.7 Задача. Докажите, что фигура подобная окружности, есть окружность.

Таким образом, мы пришли к выводу, что A’B’ = k AB. А это означает, что расстояние между любыми двумя точками окружности F’ в k раз больше, чем расстояние между подобными точками в окружности F, т.е фигуру F’ можно получить преобразованием подобия или гомотетией относительно точки О. А это значит, что окружности F и F’ подобны.

Пример 2

У треугольников АВС и А₁В₁С₁ ∠A = ∠A₁, ∠B = ∠B₁. AB = 6, AC = 9, A₁B₁ = 10, B₁C₁ = 10. Найдите остальные стороны треугольников.

Решение:

Пусть даны два треугольника АВС и А₁В₁С₁ ∠A = ∠A₁, ∠B = ∠B₁ (Рис.8). Данные треугольники подобны по двум углам: ∠A = ∠A₁ и ∠В = ∠B₁. Отсюда следует, что все стороны второго треугольника отличаются от сторон первого треугольника в k число раз, т.е. коэффициент подобия. Найдем число k:

k = AB / А₁В₁ = 6 / 10 = 3 / 5

Отсюда следует, что

ВС = k * В₁С₁ = (3 / 5) * 10 = 6 см

А₁С₁ = АС / k = 9 / (3 / 5) = 15 см

Рис.8 Задача. У треугольников АВС и А₁В₁С₁.

Пример 3

В трапеции ABCD основание АD = 32 см, а основание ВС = 8 см. Угол между диагональю АС и стороной СD равен углу ∠АВС, т.е. ∠АВС = ∠АСD. Найдите диагональ АС.

Решение:

В трапеции два основания лежат на параллельных прямых (Рис.9). Отсюда следует, что угол ∠CAD = ∠BCA, как внутренние накрест лежащие углы. Следовательно, треугольники АВС и АСD подобны по двум углам: ∠AВС = ∠АCD по условию задачи, ∠CAD = ∠BCA, как внутренние накрест лежащие углы.

Тогда можно составить следующие соотношение:

Рис.9 Задача. В трапеции ABCD основание АD = 32 см.

Пример 4

В остроугольном треугольнике АВС проведены высоты AD, BE, CF. Найдите углы треугольника DEF, если в треугольнике АВС ∠А = α, ∠В = β, ∠С = γ.

Решение:

Рассмотрим два прямоугольных треугольника AFC и ABE. Они подобны по одному острому углу, так как угол при вершине А у них общий. Следовательно, угол ∠FCE = ∠ABE. Обозначим его как ϕ₃. Аналогичным образом обозначим:

Рассмотрим два прямоугольных треугольника AFO и DOC. Они подобны по одному острому углу: углы при вершине О равны как вертикальные (Рис.10). Отсюда следует, что треугольники FOD и AOC также подобны по двум пропорциональным сторонам и углу между ними.

Так как OD / OF = OC / AO

Следовательно, OD / OС = OF / AO

Отсюда следует равенство углов:

Треугольники BFO и EOC подобны. У них углы при вершине О равны как вертикальные, а углы при вершинах F и E прямые. Отсюда следует подобие треугольников FOE и BOC. Следовательно,

Рис.10 Задача. В остроугольном треугольнике АВС.

Так как ϕ₁ + ϕ₂ + ϕ₃ = 90° (из прямоугольного треугольника BFC), то в треугольнике FDE угол при вершине F равен:

Аналогичным образом выводится, что:

Пример 5

В треугольник ABC вписан ромб ADEF, таким образом, что угол А у них общий, а вершина Е находится на стороне ВС. АВ = 12 см, АС = 4 см. Найдите сторону ромба.

Решение:

Так как у ромба противоположные стороны параллельны, то треугольники АВС и DBE подобны по двум углам: ∠А = ∠D, ∠C = ∠E как соответственные (Рис.11).

Тогда можно составить следующие соотношение:

Рис.11 Задача. В треугольник ABC вписан ромб ADEF.

Источник

• ← какие фигуры в городках есть
• какие фигуры в пространстве называются равными →

Главная > Учебные материалы > Математика: Планиметрия. Страница 9
Рис.1 Преобразование подобия и его свойства. 2.Подобие фигур. Подобие треугольников по двум углам Две фигуры называются подобными, если преобразованием подобия они переходят друг в друга. (Рис.2) Если две фигуры подобны третьей, то они подобны друг другу. Из свойств преобразования подобия следует, что у подобных фигур, соответсвующие стороны пропорциональны и соответствующие углы равны. Рис.2 Подобие фигур. Подобие треугольников по двум углам Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (Рис.3) Докажем это утверждение. Пусть даны два треугольника ABC и A’B’C’. Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. Полученный треугольник A»B»C» равен треугольнику ABC по стороне и прилегающим к ней углам. Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. А т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’. Рис.3 Подобие треугольников по двум углам. 3.Подобие треугольников по двум сторонам и углу между ними Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны. Докажем это утверждение. (Доказательство аналогично доказательству подобия по двум углам) Пусть даны два треугольника ABC и A’B’C’. Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. Полученный треугольник A»B»C» равен треугольнику ABC по двум сторонам и углу между ними со сторонами kA’B’=A»B» и kA’C’=A»C». Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. А т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’, т.е. kA’B’=AB, kB’C’=BC и kA’C’=AC.	Рис.3 Подобие треугольников. 4.Подобие треугольников по трем сторонам Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. Доказательство. (Доказательство аналогично доказательству подобия по двум углам) Пусть даны два треугольника ABC и A’B’C’. Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. В результате получим треугольник A»B»C», который равен треугольнику ABC по трем сторонам kA’B’=A»B», kВ’C’=В»C» и kA’C’=A»C». Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. И т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’.	Рис.4 Подобие треугольников по трем сторонам. 5.Подобие прямоугольных треугольников Если два прямоугольных треугольника имеют по одному равному острому углу, то такие треугольники подобны. Пусть дан прямоугольный треугольник ABC. Проведем высоту CD. Треугольники ABC и ADC подобны, т.к. угол А у них общий. Так же как и треугольники ADC и BDC. Следовательно: Т.е. катет прямоугольного треугольника равен средней геометрической гипотенузы и проекции этого катета на гипотенузу. А высота в прямоугольном треугольнике равна средней геометрической между проекциями катетов на гипотенузу. Отсюда можно сделать вывод, что в любом треугольнике биссектриса делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. (Свойство биссектрисы треугольника).	Рис.5 Подобие прямоугольных треугольников. Т.е. отрезки AD и DC пропорциональны сторонам AB и BC.	Рис.6 Подобие прямоугольных треугольников.