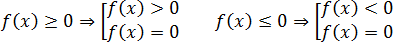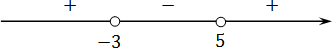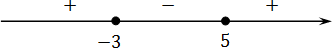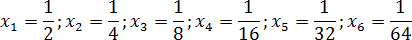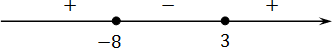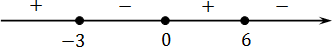какие скобки ставить при решении неравенств

Метод интервалов: случай нестрогих неравенств

Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:

— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:

В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.

Отрезки и интервалы: в чем разница?

Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:

Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:

На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.

Метод интервалов для нестрогих неравенств

К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:

Задача. Решите строгое неравенство:

Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:

( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

Отмечаем полученные корни на координатной оси:

Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:

Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:

Задача. Решите нестрогое неравенство:

Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:

( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

Отмечаем полученные корни на координатной оси:

В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:

Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:

Итак, основное отличие строгих и нестрогих неравенств:

Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.

Почему бесконечности всегда стоят в круглых скобках

У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем

Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.

— это гипотетическое число, которое больше любого другого числа, участвующего в решении.

Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.

Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.

Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:

Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:

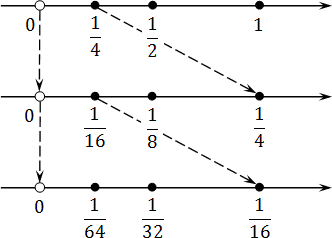
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:

Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.

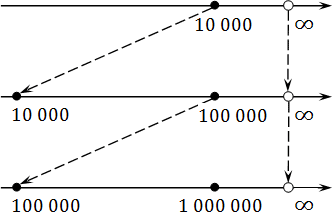
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:

Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.

Примеры решения неравенств

В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.

Как обычно, приравниваем все к нулю:

( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.

Теперь рассматриваем функцию, которая находится в левой части неравенства:

Подставим в эту функцию бесконечность — получим выражение вида:

Чертим координатную ось, отмечаем корни и расставляем знаки:

Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:

x (12 − 2 x )(3 x + 9) ≥ 0

x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.

x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].

Источник

Как записать ответ неравенства

Впрочем, мы рекомендуем освоить запись ответа неравенства в математических обозначениях сразу, так как в любом случае в старшей школе и затем в университете будут требовать именно такую запись ответа.

Перед разбором, как записывать ответ неравенства математическими знаками, вспомним расшифровку и обозначение этих знаков.

Перейдем к непосредственной записи ответа неравенства. Рассмотрим и решим линейное неравенство.

Мы решили линейное неравенство, теперь запишем его ответ с помощью математических знаков.

Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.

Итак, мы изобразили ответ неравенства на числовой оси. После этого запишем слово «Ответ:» и за ним запишем « x ∈ ». Такая запись читается как «икс принадлежит».

Взглянув на рисунок ответа на числовой оси, мы видим, что область решений начинается с числа « 14 ». Число « 14 » не входит в область решений («пустая» точка на оси). Значит, используем круглую скобку.

Нам остается понять, где заканчивается область решений справа. Правильный ответ — справа область заканчивается в положительной бесконечности « + ∞ ».

На числовой оси на обоях краях слева и справа соответственно расположены «минус» и «плюс» бесконечности. Как правило, их не рисуют на числовой оси лишний раз, т.к. их наличие на оси подразумевается.

Запишем окончательный ответ.

Знаки « + ∞ » и « − ∞ » всегда записываются с круглыми скобками.

Разберем другой пример.

Также как и в предыдущем примере всегда начинаем записывать
ответ с записи « x ∈… ».

В ответе « x ≤ 8 » область решений начинается с « − ∞ » и заканчивается на « 8 », которое входит в ответ. Значит, « 8 » будет с квадратной скобкой. Так и запишем в ответе.

Запись ответа неравенства для квадратных неравенств

При решении квадратных неравенств часто может получаться несколько интервалов в ответе. Разберемся, как их записывать в ответ. Рассмотрим пример квадратного неравенства и его решение.

x 2 − 3x + 2 3 2 − 4 · 1 · 22 · 1

x_1;2 =

Рассмотрим другой пример квадратного неравенства и его решения.

x_1;2 =

x_1;2 =

В ответе неравенства мы получили два интервала в области решений
(x ≤ −1; x ≥ 3) и оба интервала нужно записать в ответ. Запись ответа неравенства всегда делается слева направо (как мы привыкли читать).

Начнем слева направо записывать интервалы в ответ. Первый интервал начинается с «минус» бесконечности и заканчивается на « −1 » (включительно). Так и запишем.

Второй интервал начинается с « 2 »(включительно) и заканчивается на «плюс» бесконечности. Для объединения интервалов используем знак « ∪ » («объединение»).

Источник

Метод интервалов, решение неравенств

Определение квадратного неравенства

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

Квадратное неравенство можно решить двумя способами:

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Неравенство примет вид:

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Алгебра. Урок 8. Неравенства, системы неравенств.

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x b a x ≤ b a x > b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Смысл жирной точки в том, что сама точка входит в ответ.

Таблица числовых промежутков

Алгоритм решения линейного неравенства

a x b a x ≤ b a x > b a x ≥ b

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

Квадратные неравенства

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№5. Решить неравенство x 2 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

3 ( x + 8 ) − 5 \ x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

x = − 37 5 = − 37 5 = − 7,4

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

Алгоритм решения системы неравенств

Примеры решений систем неравенств:

№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 4 на графике жирная, так как знак неравенства нестрогий.

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Графическая интерпретация решения:

№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения:

Графическая интерпретация решения:

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения первого неравенства:

Решаем методом интервалов.

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Источник

• ← какие скобки при нестрогом неравенстве
• какие скобки ставятся при строгом неравенстве →