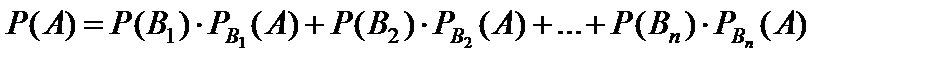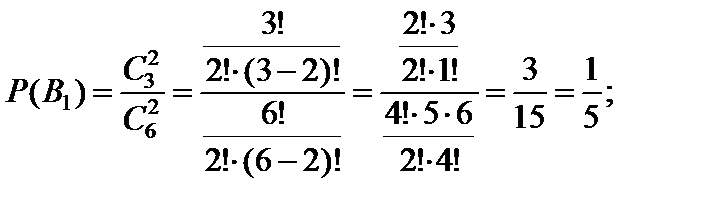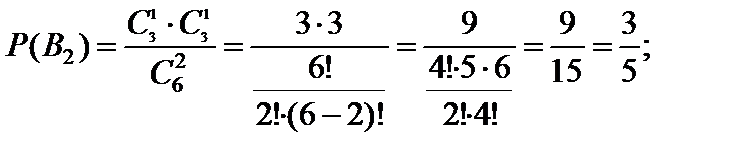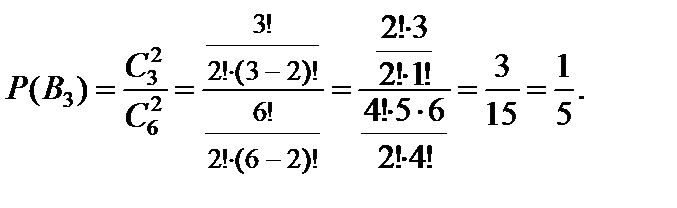какие события называются гипотезами

Формула полной вероятности. Формула Байеса

Пусть событие A может наступить при условии появления одного из несовместных событий B₁, B₂, …, B_n, образующих полную группу. Так как заранее не известно, какое из этих событий наступит, их называют гипотезами. Тогда вероятность события A вычисляется по формуле полной вероятности:

,

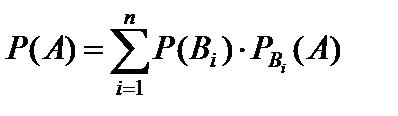
P_Bi(A) – условная вероятность события A при этой гипотезе.

Если до испытания вероятности гипотез были P(B₁), P(B₂), …, P(B_n), а в результате испытания появилось событие A, то с учетом этого события «новые», т. е. условные, вероятности гипотез вычисляются по формуле Байеса:

.

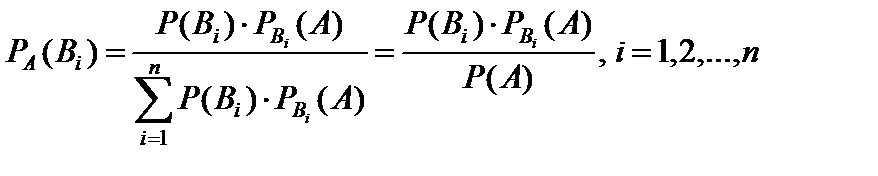
Формула Байеса дает возможность произвести переоценки вероятностей гипотез B₁, B₂, …, B_n после того, как стало известно, что событие 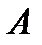наступило.

Тест 1.18. Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,04 и 0,13 – в период экономического кризиса. Предположим, что вероятность того, что начнется период экономического роста, равна 0,65. Количество гипотез события «случайно выбранный клиент банка не вернет полученный кредит», равно:

Обозначим через A событие, состоящее в том, что куплена стандартная лампа, B₁ – «лампа изготовлена на первом заводе», B₂ – «лампа изготовлена на втором заводе».

Из условия следует, что

; ;

; .

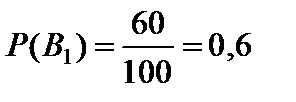
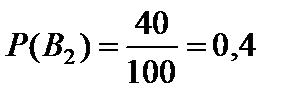
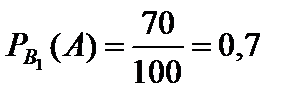
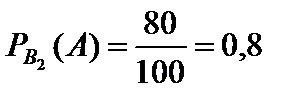
По формуле полной вероятности имеем:

.

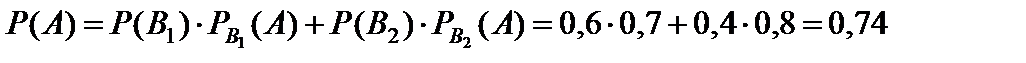
Тест 1.19. Издательство разослало рекламные материалы на новый учебник по бухгалтерскому учету, которые получили 80% профессоров, читающих этот курс в различных высших учебных заведениях. Отобрали эту книгу и приняли ее для преподавания 30% профессоров, получивших рекламные материалы и 10% не получивших их. Вероятность того, что случайно выбранный профессор вуза принял этот учебник для преподавания, равна:

2) ;

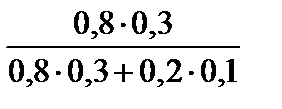
Пример 1.39. В студенческой группе 70% – юноши, 20% юношей и 40% девушек имеют сотовый телефон. После занятий в аудитории был найден кем-то забытый телефон. Какова вероятность того, что он принадлежал юноше?

Пусть событие A состоит в том, что после занятий в аудитории был найден кем-то забытый телефон. Тогда в качестве гипотез примем события B₁ – «найденный телефон принадлежал юноше» и B₂ – «найденный телефон принадлежал девушке». Из условия следует, что

; ;

; .

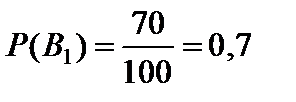
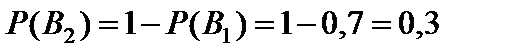
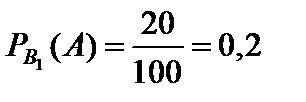
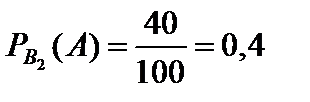
В соответствии с формулой Байеса находим искомую вероятность:

0,54.

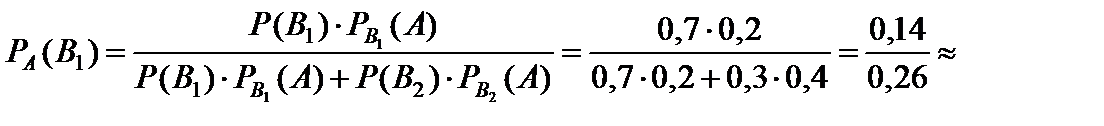
Ответ: 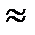0,54.

Тест 1.20. Медицинский тест на возможность вирусного заболевания дает следующие результаты:

1. Если проверяемый болен, то тест даст положительный результат с вероятностью 0,92.

2. Если проверяемый не болен, то тест может дать положительный результат с вероятностью 0,04.

Поскольку заболевание редкое, то ему подвержены только 0,1% населения. Предположим, что некоторому случайно выбранному человеку сделан анализ и получен положительный результат. Вероятность того, что человек действительно болен, равна:

1) ;

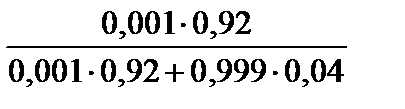
2) ;

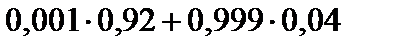
4) ;

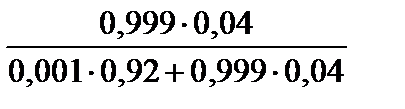
5) .

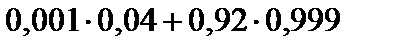
Пример 1.40. В коробке 3 новых и 3 уже использованных теннисных мяча. Для первой игры наудачу берут из коробки 2 мяча и затем их возвращают в коробку. Какова вероятность для второй игры из этой коробки наудачу вынуть два новых мяча?

События B₁, B₂, B₃ образуют полную группу несовместных событий, при этом:

Для контроля можно найти сумму вероятностей гипотез, она должна равняться единице: .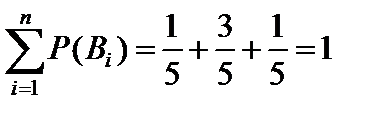

Далее имеем: ; ; .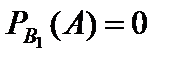

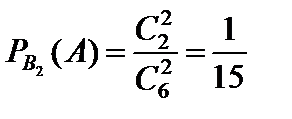
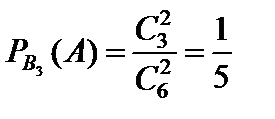
Теперь, используя формулу полной вероятности, найдем:

Тест 1.21. На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0,95. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0,02. Реальная вероятность аварийной ситуации равна 0,004. Предположим, что звуковой сигнал сработал. Вероятность реальной аварийной ситуации находится с помощью формулы:

1) полной вероятности;

Вопросы для самоконтроля

1. Что называют испытанием?

2. Что называют событием?

3. Какое событие называют достоверным в данном испытании?

4. Какое событие называют невозможным в данном испытании?

5. Какое событие называют случайным в данном испытании?

6. Что называют элементарным событием?

7. Какие события называют совместными в данном испытании?

8. Какие события называют несовместными в данном испытании?

9. Какие события образуют полную группу событий?

10. Какие события считают равновозможными?

11. Какие события называют противоположными?

12. Что называют суммой двух событий?

13. Что называют произведением двух событий?

14. Что называют перестановками?

15. По какой формуле вычисляют число перестановок из n различных элементов?

16. Что называют размещениями?

17. По какой формуле вычисляют число размещений из n различных элементов по m элементов?

18. Что называют сочетаниями?

19. По какой формуле вычисляют число сочетаний из n элементов по m элементов?

20. Что называют вероятностью события?

21. Чему равна вероятность достоверного события?

22. Чему равна вероятность невозможного события?

23. В каких пределах заключена вероятность любого события?

24. Что такое частота события?

25. Какое определение вероятности называют статистическим?

26. Какими свойствами обладает статистическая вероятность?

27. Как определяется геометрическая вероятность в общем случае?

28. Чему равна вероятность суммы двух совместных событий?

29. Чему равна вероятность суммы двух несовместных событий?

30. как формируется теорема о вероятности суммы n несовместных событий.

31. Чему равна вероятность произведения двух независимых событий?

32. Чему равна вероятность произведения двух зависимых событий?

33. Что такое условная вероятность?

34. Как найти вероятность появления хотя бы одного из n независимых событий, имеющих одинаковые вероятности?

35. Какие события называются гипотезами?

36. Какие события образуют полную группу событий?

37. При каких условиях применяется формула полной вероятности?

38. Как изменяются вероятности гипотез, если известно, что событие произошло?

Источник

Тест с ответами по теории вероятности

1.Указать верное определение.Суммой двух событий называется:

а ) Новое событие, состоящее в том, что происходят оба события одновменно;

б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;+

в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.

а ) Новое событие, состоящее в том, что происходят оба события одновременно;+

б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;

в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.

а ) Произведение числа исходов, благоприятствующих появлению события на общее число исходов;

б ) Сумма числа исходов, благоприятствующих появлению события и общего числа исходов;

в ) Отношение числа исходов, благоприятствующих появлению события к общему числу исходов;+

а ) больше нуля и меньше единицы;

а ) больше нуля и меньше единицы;

а ) больше нуля и меньше единицы;+

а ) Вероятность суммы событий равна сумме вероятностей этих событий;

б ) Вероятность суммы независимых событий равна сумме вероятностей этих событий;

в ) Вероятность суммы несовместных событий равна сумме вероятностей этих событий;+

а ) Вероятность произведения событий равна произведению вероятностей этих событий;

б ) Вероятность произведения независимых событий равна произведению вероятностей этих событий;+

в ) Вероятность произведения несовместных событий равна произведению вероятностей этих событий;

а ) Элементарный исход;

б ) Пространство элементарных исходов;

в ) Подмножество множества элементарных исходов.+

а ) любые попарно несовместные события;

б ) попарно несовместные события, объединение которых образует достоверное событие;+

в ) пространство элементарных событий.

а ) априорную вероятность гипотезы,

б ) апостериорную вероятность гипотезы,

в ) вероятность гипотезы.+

а) невозрастающей; б) неубывающей; +в) произвольного вида.

а) независимых+; б) зависимых; в) всех.

а) независимых;+ б) зависимых; в) всех.

а) отсутствует функциональная зависимость между Х и Y;

б) величины Х и Y независимы;+

в) отсутствует линейная корреляция между Х и Y;

а) указывая её вероятности;

б) указывая её закон распределения;+

в) поставив каждому элементарному исходу в соответствие

а) начальный момент первого порядка;+

б) центральный момент первого порядка;

в) произвольный момент первого порядка.

а) начальный момент второго порядка;

б) центральный момент второго порядка;+

в) произвольный момент второго порядка.

а) значение случайной величины при котором вероятность равняется 0,5;

б) значение случайной величины при котором либо вероятность, либо функция плотности достигают максимального значения ;+

в) значение случайной величины при котором вероятность равняется 0.

а) если все варианты увеличить в одно и тоже число раз, то и дисперсия увеличится в такое же число раз.

б) дисперсия постоянной равняется нулю.

в) если все варианты увеличить на одно и тоже число, то выборочная дисперсия не изменится.+

а) Представление наблюдений в качестве независимых случайных величин имеющих один и тот же закон распределения.

б) совокупность результатов наблюдений;

в) всякую функцию результатов наблюдения.+

а) Метод максимального правдоподобия используется для получения оценок;

б) Выборочная дисперсия является смещенной оценкой для дисперсии;

в) В качестве статистических оценок параметров используются несмещённые, несостоятельные, эффективные оценки.+

а) По многомерной функции распределения всегда можно найти одномерные (маргинальные) распределения отдельных компонент.

б) По одномерным (маргинальным) распределениям отдельных компонент всегда можно найти многомерную функцию распределения.

в) По многомерной функции плотности всегда можно найти одномерные (маргинальные) плотности распределения отдельных компонент.

а) Закон распределения случайной величины X не зависит от того, какое значение приняла случайная величина Y.

в) коэффициент корреляции между случайными величинами X и Y равен нулю.

а) аналогом формулы Байеса для непрерывных случайных величин;

б) аналогом формулы полной вероятности для непрерывных случайных величин;+

в) аналогом формулы произведения вероятностей независимых событий для непрерывных случайных величин.

а) выборка и группировка статистических данных, полученных в результате эксперимента;

б) определение параметров распределения, вид которого заранее известен;+

в) получение оценки вероятности изучаемого события.

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличное онлайн обучение по математике для учеников с 1 по 11 классы, записывайся на пробное занятие!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник