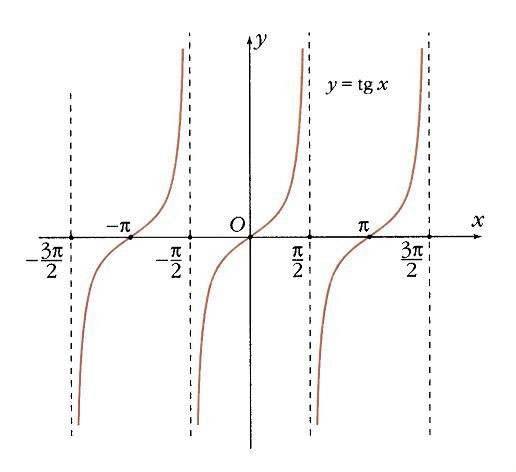
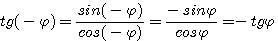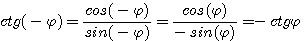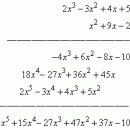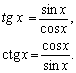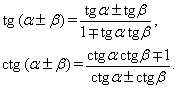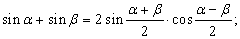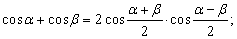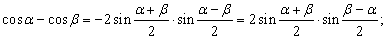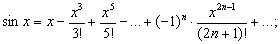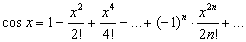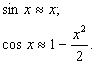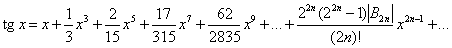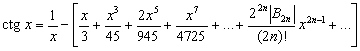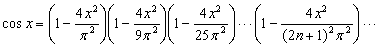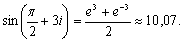какие тригонометрические функции являются нечетными функциями
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №2 Чётность и нечётность тригонометрических функций. Периодичность.
Перечень вопросов, рассматриваемых в теме
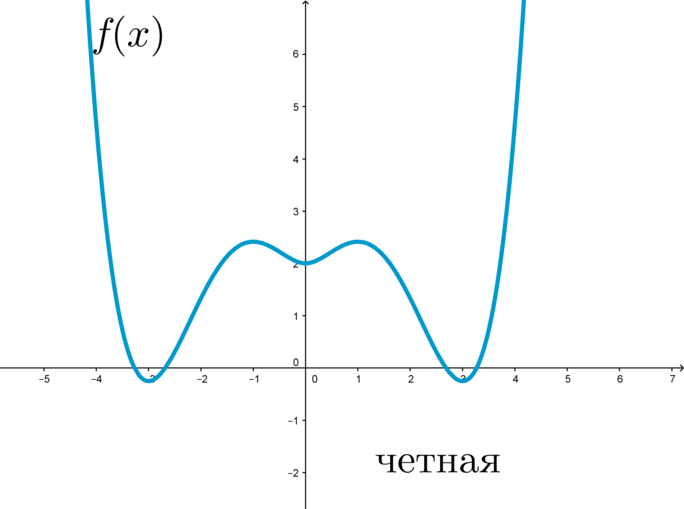
Функцию y=f(x), x∈X называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x).
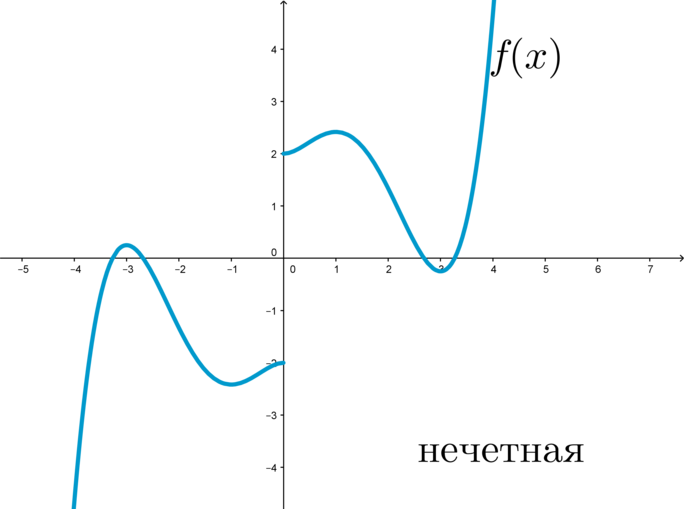
Функцию y=f(x), x∈X называют нечётной, если для любого значения x из множества X выполняется равенство f(−x)=−f(x).
Период функций, представляющих собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |ОА| к длине гипотенузы |ОВ|.
Область. определения функции (D) — множество R всех действительных чисел
Множество значений функции (E) — отрезок [-1; 1], т.е. косинус функция —ограниченная.
Для того, чтобы определить чётность функции косинус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, cos(60°) = ½ = cos(–60°)–это значит, что : cos(−x)=cos x для всех x∈R и у=сosx–чётная
Сиинус(sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |АВ| к длине гипотенузы |ОВ|.
Область определения функции (D) — множество R всех действительных чисел.
Множество значений функции (E) — отрезок [-1; 1], т.е. синус функция —ограниченная.
Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, sin(30°) = ½ sin(–30°) = –½ –это значит, что : sin(−x)=–sin (x) для всех x∈R и y=sinx–нечётная


Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Выясним, является ли функция
чётной или нечётной?
Пример 2. Доказать, что число 2π является наименьшим положительным периодом функции y=cos x
Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2π
Доклад «Четность, нечетность, периодичность тригонометрических функций»
Ищем педагогов в команду «Инфоурок»
Четность, нечетность, периодичность тригонометрических функций
Четная функция – это Функция y = f ( x ) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство f (- x ) = f ( x ) Свойства: симметричен относительно оси координат.
Практическое задание: как определить четная функция или не четная?
Рассмотрим следующий рисунок (рис. 1):
Периодичность тригонометрических функций
Практическое задание: как узнать является ли функция периодичной?
Рассмотрим рисунок (2)
Примеры задач на использование четности, нечетности и периодичности тригонометрических функций
Является ли функция y =2+ sin ^2 x
y(-x) =2+sin^2(-x) =2+(-sin x) ^2 = 2+sin^2 x=y(x)>
Доказать, что f(x) = Sin 3x – периодическая функция с периодом (2 π) /3.
Данная функция определена для всех x є R, поэтому достаточно показать, что для любого x верно равенство f (x + T) = f(x).
f(x + (2 π )/3) = Sin 3(x + (2 π )/3) = Sin (3x + 2 π ) = Sin 3x = f(x)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-1517110
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Приамурье начнут пускать на занятия только привитых студентов
Время чтения: 0 минут
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
МГПУ вводит QR-коды для посещения очных занятий
Время чтения: 1 минута
Студенты Хабаровского края перейдут на дистанционное обучение
Время чтения: 1 минута
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
Рособрнадзор оставил за регионами решение о дополнительных школьных каникулах
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Четные и нечетные функции
График четной функции симметричен относительно оси \(y\) :
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
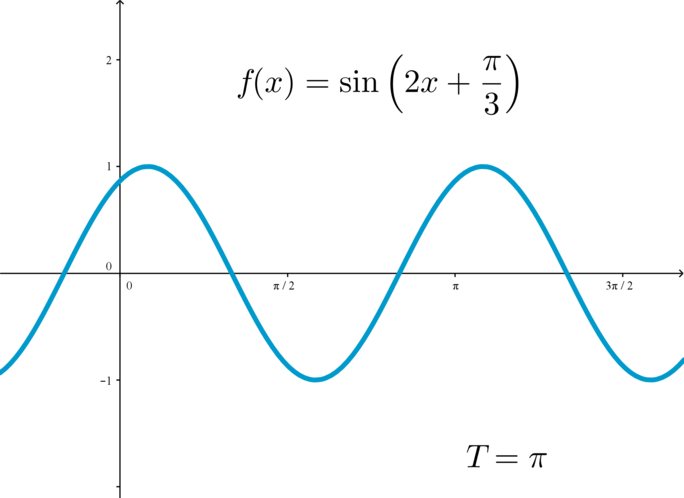
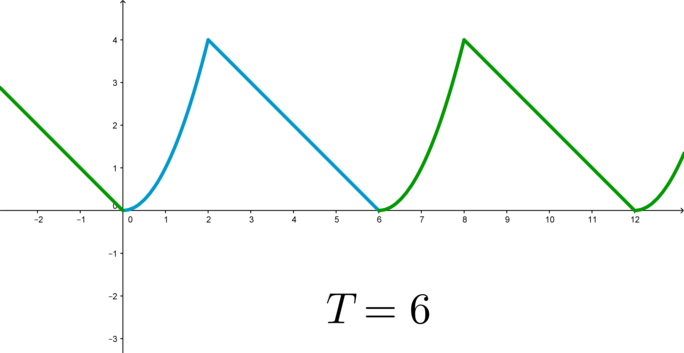
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Какие тригонометрические функции являются нечетными функциями
ЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
Четность тригонометрических функций.
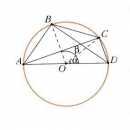
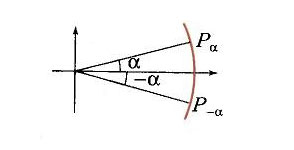
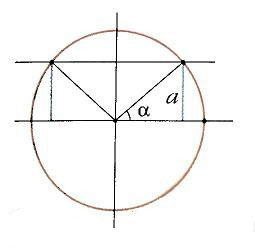
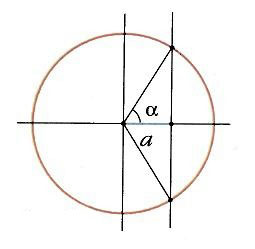
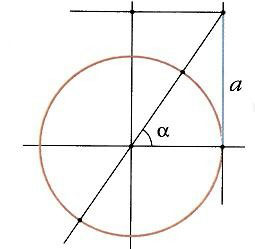
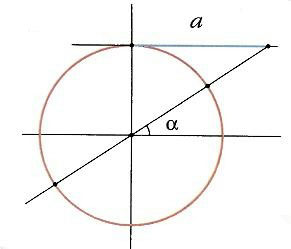
Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки).
Поэтому конечные стороны OA 1 и ОА 2 этих углов симметричны относительно оси абсцисс.
Следовательно, синус является нечетной, а косинус — четной функцией угла.
Поэтому тангенс и котангенс являются нечетными функциями угла.
Выяснить, какие из данных функций являются четными и какие нечетными:
1) у = sin (—х); 4) у = sin x cos х; 7) у = sin 2 x;
2) у = cos (—х); 5) у = sec x; 8) у = cos 2 x;
3) у = tg (2х); 6) у = cosec x; 9) у = sin x + tg x.
Периодичность функций sin φ и cos φ
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ.
Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся.
Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°.
Пусть f(х) есть некоторое выражение, зависящее от переменной величины х.
(Например, f(х) = x 2 , f(х) = sin x и т. д.)
Определяет у как функцию аргумента х.
Если при любых допустимых значениях аргумента х
где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом.
Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°.
При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ.
Таким образом, cos φ = cos (φ + 360°n),
sin φ = sin (φ + 360°n), (1)
где n — любое целое число (положительное, отрицательное или нуль).
Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов.
Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции.
Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ
В частности, при φ = 0 получаем: sinТ = sin 0° = 0.
Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = 90° мы получили бы
Аналогично можно доказать, что периодом функции cos φ также является угол в 360° Предлагаем учащимся убедиться в этом самостоятельно.
1. Доказать следующие соотношения:
а) sin 740° = sin 20°; в) cos 54° = cos (—1026°);
б) sin (—1000°) = sin 80°; г) cos (—1750°) = cos 50°.
2. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 360°:
a) sin 820°; б) cos (—7363°); в) sin (—600°).
3. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 180°:
a) cos 729°; б) sin 1268°; в) sin (— 535°); г) cos (— 1001°).
4. Доказать, что угол в 540° является одним из периодов функции у = cos2х.
5. Доказать, что угол и 360° является одним из периодов функции у = tgx.
6. Докажите, что любой период Т функции у = cos х является корнем уравнения
Верно ли обратное утверждение?
Периодичность функций tg φ и ctg φ
Следовательно, при любом φ
Это означает, что функция tg φ является периодической с периодом 180°. Но будет ли угол в 180° наименьшим жительным периодом этой функции?
Предположим, что наименьший положительный период функции tg φ равен Т. Тогда для всех допустимых значений φ должно быть
В частности, при φ = 0° получаем:
Но тангенс положительного угла равен нулю лишь тогда, когда синус этого угла равен нулю, то есть при Т = 180°, 360°, 540° и т, д. Следовательно, никакой положительный угол, меньший 180°, не может быть периодом функции tg φ. Остается признать, чтб периодом (то есть наименьшим положительным периодом) функции tg φ является угол в 180°.
Аналогично можно доказать, что периодом функции сtg φ также является угол в 180°. Предлагаем учащимся убедиться в этом самостоятельно.
1. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 180°:
a) tg 205°; б) tg (—185°); в) ctg 300°; г) ctg (—210°).
2. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 90°:
3. Доказать, что угол в 120° является одним из периодов функции у = ctg 3х.
4. Доказать, что любой период Т функции у = ctg х является корнем уравнения
Верно ли обратное утверждение?
О периодических функциях.
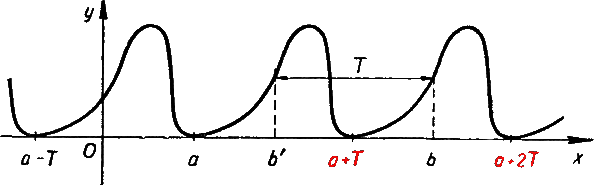
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой.
Действительно, пусть периодическая функция f(x) задана в интервале (а, а + Т), где Т — период этой функции.
Покажем, как можно определить значения этой функции в интервале ( а + Т, а + 2 T ).
Для любой точки b из этого интервала можно указать точку b‘ из интервала (а, а + T ), отстоящую от b на расстоянии T.
В силу периодичности функции f(x)
Таким образом, по заданным значениям функции f
Итак, задание периодической с периодом Т функции f(x) на любом интервале длины Т дает возможность полностью охарактеризовать ее на всей числовой прямой. Поэтому для исследования функции f(x), периодической с периодом Т, достаточно изучить ее поведение лишь на каком-нибудь интервале длины Т. Например, для исследования функций у = sin φ и у = cos φ достаточно рассмотреть их лишь при 0° <φ <360°. Для исследования функции у = tg φ можно было бы ограничиться интервалом 0° <φ <180°. Но при φ = 90° tg φ не определен. Поэтому в данном случае целесообразнее выбрать какой-нибудь другой интервал, в каждой точке которою функция у = tg φ была бы определена. Мы отдадим предпочтение интервалу —90° < φ < 90°. Однако в принципе можно было бы выбрать, конечно, и интервал 0° <φ <180°. Для изучения функции сtg φ целесообразно выбрать интервал 0° < φ < 180°.
2. Может ли периодическая с периодом Т функция f(x) удовлетворить условию
Если может, то в каком случае? Ответ пояснить примерами.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ – один из классов элементарных функций.
Функция у = cos х.
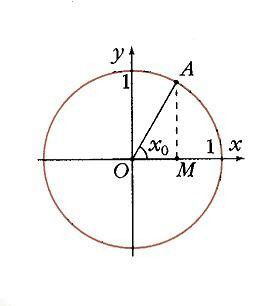
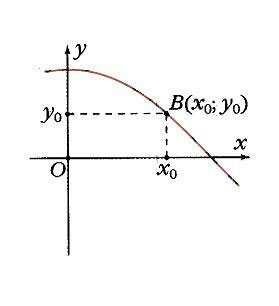
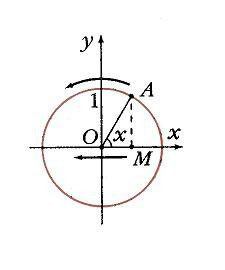
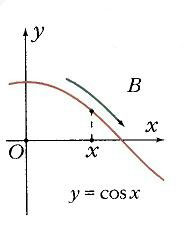
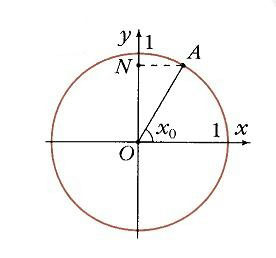
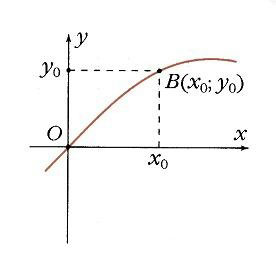
Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента x0 и отсчитать от оси Ox угол x0, то этому углу на единичной окружности соответствует некоторая точка A (рис. 1) а ее проекцией на ось Ох будет точка М. Длина отрезка ОМ равна абсолютной величине абсциссы точки A. Данному значению аргумента x0 сопоставлено значение функции y = cos x0 как абсциссы точки А. Соответственно точка В (x0; у0) принадлежит графику функции у = cos х (рис. 2). Если точка А находится правее оси Оу, то косинус будет положителен, если же левее – отрицателен. Но в любом случае точка А не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:
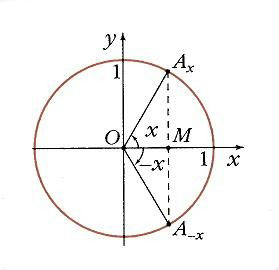
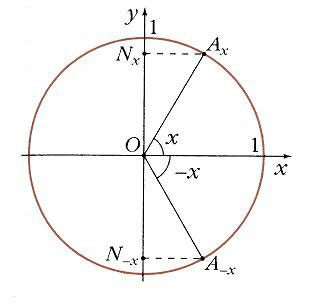
Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x и –x, найти на окружности соответствующие точки Ax и А-x. Как видно на рис. 3 их проекцией на ось Ох является одна и та же точка М. Поэтому
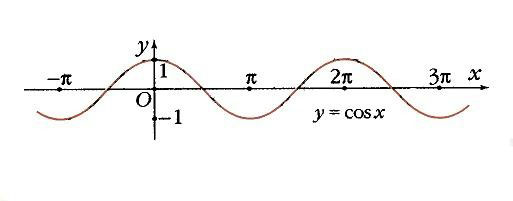
Значит, можно исследовать свойства функции y = cos х на отрезке [0, p ], а затем учесть ее четность и периодичность.
Функция y = sin х.
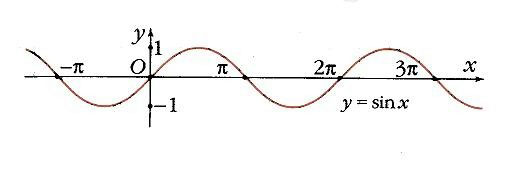
На единичной окружности углу x0 соответствует точка А (рис. 7), а ее проекцией на ось Оу будет точка N. Значение функции у0 = sin x0 определяется как ордината точки А. Точка В (угол x0, у0) принадлежит графику функции y = sin x (рис. 8). Ясно, что функция y = sin x периодическая, ее период равен 2 p :
т.е. синус – функция нечетная, f(–x) = –f(x) (рис. 9).
Если точку A повернуть относительно точки О на угол p /2 против часовой стрелки (другими словами, если угол х увеличить на p /2), то ее ордината в новом положении будет равна абсциссе в старом. А значит,
Иначе, синус – это косинус, «запоздавший» на p /2, поскольку любое значение косинуса «повторится» в синусе, когда аргумент возрастет на p /2. И чтобы построить график синуса, достаточно сдвинуть график косинуса на p /2 вправо (рис. 10). Чрезвычайно важное свойство синуса выражается равенством
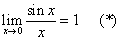
Геометрический смысл равенства виден из рис. 11. Здесь х – это половина дуги АВ, а sin х – половина соответствующей хорды. Очевидно, что по мере сближения точек А и В длина хорды все точнее приближается к длине дуги. Из того же рисунка несложно извлечь неравенство
Функции у = tg х, у = ctg х. Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:
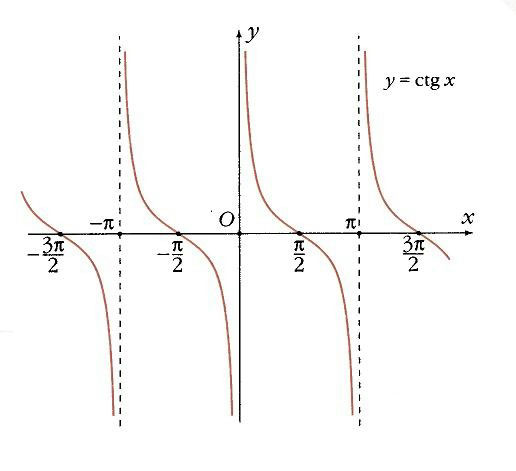
Котангенс не определен там, где синус равен 0 (когда х = k p ). В остальных точках он монотонно убывает, а прямые х = k p – его вертикальные асимптоты. В точках х = p /2 + k p котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).
Четность и периодичность.
Функция называется четной, если f(–x) = f(x). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:
| sin (–α) = – sin α | tg (–α) = – tg α |
| cos (–α) = cos α | ctg (–α) = – ctg α |
| sec (–α) = sec α | cosec (–α) = – cosec α |
| sin (α + 2kπ) = sin α | cos (α + 2kπ) = cos α |
| tg (α + kπ) = tg α | ctg (α + kπ) = ctg α |
| sec (α + 2kπ) = sec α | cosec (α + 2kπ) = cosec α |
Периодичность синуса и косинуса следует из того, что все точки P a + 2k p , где k = 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки P a + k p поочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.
Основные свойства тригонометрических функций могут быть сведены в таблицу:
Формулы приведения.
 – a
– a + a
+ a + a
+ a + a
+ a1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
Формулы сложения.
sin ( a 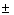
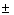
cos ( a 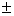
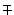
Формулы кратных углов.
Эти формулы выводятся прямо из формул сложения:
sin 2 a = 2 sin a cos a ;
cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a ;
sin 3 a = 3 sin a – 4 sin 3 a ;
cos 3 a = 4 cos 3 a – 3 cos a ;
Если в формулах двойного аргумента заменить a на a /2, их можно преобразовать в формулы половинных углов:
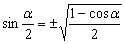
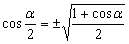
Формулы универсальной подстановки.
Используя эти формулы, выражение, включающее разные тригонометрические функции от одного и того же аргумента, можно переписать как рациональное выражение от одной функции tg ( a /2), это бывает полезно при решении некоторых уравнений:
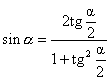 | 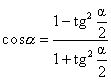 |
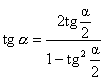 | 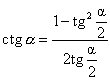 |
Формулы преобразования сумм в произведения и произведений в суммы.
До появления компьютеров эти формулы использовались для упрощения вычислений. Расчеты производились с помощью логарифмических таблиц, а позже – логарифмической линейки, т.к. логарифмы лучше всего приспособлены для умножения чисел, поэтому все исходные выражения приводили к виду, удобному для логарифмирования, т.е. к произведениям, например:
2 sin a sin b = cos ( a – b ) – cos ( a + b );
2 cos a cos b = cos ( a – b ) + cos ( a + b );
2 sin a cos b = sin ( a – b ) + sin ( a + b ).
Формулы для функций тангенса и котангенса можно получить из вышеприведенных.
Формулы понижения степени.
Из формул кратного аргумента выводятся формулы:
| sin 2 a = (1 – cos 2 a )/2; | cos 2 a = (1 + cos 2 a )/2; |
| sin 3 a = (3 sin a – sin 3 a )/4; | cos 3 a = (3 cos a + cos 3 a )/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
(tg x)` = 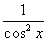 ; ; | (ctg x)` = – 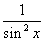 ; ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.
Представление тригонометрических функций в виде степенных рядов и бесконечных произведений.
Все тригонометрические функции допускают разложение в степенные ряды. При этом функции sin x b cos x представляются рядами. сходящимися для всех значений x:
Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях x:
Функции sin x и cos x могут быть представлены в виде бесконечных произведений:
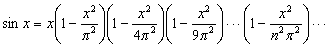
Тригонометрические функции комплексного аргумента
определяются как аналитические продолжения соответствующих тригонометрических функций действительного аргумента в комплексную плоскость. Так, sin z и cos z могут быть определены с помощью рядов для sin x и cos x, если вместо x поставить z:
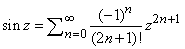
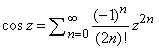
Эти ряды сходятся по всей плоскости, поэтому sin z и cos z – целые функции.
Тангенс и котангенс определяются формулами:
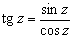
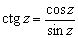
Функции tg z и ctg z – мероморфные функции. Полюсы tg z и sec z – простые (1-го порядка) и находятся в точках z = p /2 + p n, полюсы ctg z и cosec z – также простые и находятся в точках z = p n, n = 0, ±1, ±2,…
Все формулы, справедливые для тригонометрических функций действительного аргумента, справедливы и для комплексного. В частности,
т.е. четность и нечетность сохраняются. Сохраняются и формулы
т.е. периодичность также сохраняется, причем периоды такие же, как и для функций действительного аргумента.
Тригонометрические функции могут быть выражены через показательную функцию от чисто мнимого аргумента:
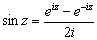
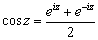
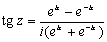
Обратно, e iz выражается через cos z и sin z по формуле:
Эти формулы носят название формул Эйлера. Леонард Эйлер вывел их в 1743.
Тригонометрические функции также можно выразить через гиперболические функции:
z = –i sh iz, cos z = ch iz, z = –i th iz.
где sh, ch и th – гиперболические синус, косинус и тангенс.
Тригонометрические функции комплексного аргумента z = x + iy, где x и y – действительные числа, можно выразить через тригонометрические и гиперболические функции действительных аргументов, например:
Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:
Если неизвестный угол входит в уравнение как аргумент тригонометрических функций, то уравнение называется тригонометрическим. Такие уравнения настолько часто встречаются, что методы их решения очень подробно и тщательно разработаны. С помощью различных приемов и формул тригонометрические уравнения сводят к уравнениям вида f(x) = a, где f – какая-либо из простейших тригонометрических функций: синус, косинус, тангенс или котангенс. Затем выражают аргумент x этой функции через ее известное значение а.
Поскольку тригонометрические функции периодичны, одному и тому же а из области значений отвечает бесконечно много значений аргумента, и решения уравнения нельзя записать в виде одной функции от а. Поэтому в области определения каждой из основных тригонометрических функций выделяют участок, на котором она принимает все свои значения, причем каждое только один раз, и находят функцию, обратную ей на этом участке. Такие функции обозначают, приписывая приставку агс (дуга) к названию исходной функции, и называют обратными тригонометрическими функциями или просто аркфункциями.
Обратные тригонометрические функции.
Для sin х, cos х, tg х и ctg х можно определить обратные функции. Они обозначаются соответственно arcsin х (читается «арксинус x»), arcos x, arctg x и arcctg x. По определению, arcsin х есть такое число у, что
Аналогично и для других обратных тригонометрических функций. Но такое определение страдает некоторой неточностью.
Если отразить sin х, cos х, tg х и ctg х относительно биссектрисы первого и третьего квадрантов координатной плоскости, то функции из-за их периодичности становятся неоднозначными: одному и тому же синусу (косинусу, тангенсу, котангенсу) соответствует бесконечное количество углов.
Так же решаются другие простейшие тригонометрические уравнения:
где п = 0, ±1, ±2. (рис. 16);
где п = 0, ±1, ±2. (рис. 17);
где п = 0, ±1, ±2. (рис. 18).
Основные свойства обратных тригонометрических функций:
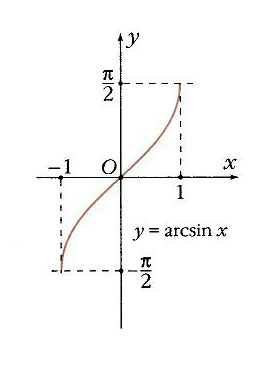
arcsin х (рис. 19): область определения – отрезок [–1, 1]; область значений – [– p /2, p /2], монотонно возрастающая функция;
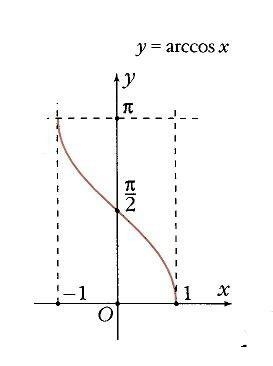
arccos х (рис. 20): область определения – отрезок [–1, 1]; область значений – [0, p ]; монотонно убывающая функция;
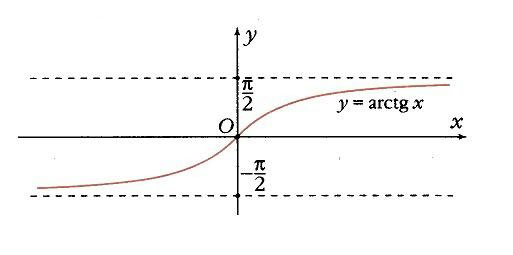
arctg х (рис. 21): область определения – все действительные числа; область значений – интервал (– p /2, p /2); монотонно возрастающая функция; прямые у = – p /2 и у = p /2 – горизонтальные асимптоты;
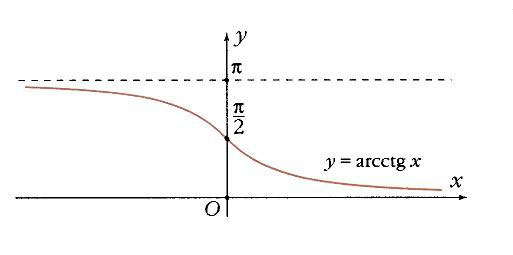
arcctg х (рис. 22): область определения – все действительные числа; область значений – интервал (0, p ); монотонно убывающая функция; прямые y = 0 и у = p – горизонтальные асимптоты.
Т.к. тригонометрические функции комплексного аргумента sin z и cos z (в отличие от функций действительного аргумента) принимают все комплексные значения, то и уравнения sin z = a и cos z = a имеют решения для любого комплексного a:
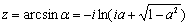
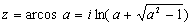
Функции tg z и ctg z принимают все комплексные значения, кроме ±i: уравнения tg z = a, ctg z = a имеют решения для любого комплексного числа a № ± i:
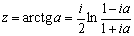
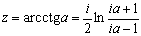
Для любого z = x + iy, где x и y – действительные числа, имеют место неравенства
из которых при y ® Ґ вытекают асимптотические формулы (равномерно относительно x)
Кочетков Е.С., Кочеткова Е. С. Алгебра и элементарные функции, ч. 1–2, М., 1966
Шабат Б.В. Введение в комплексный анализ. М., 1969