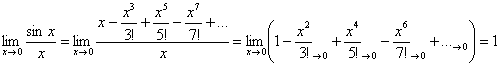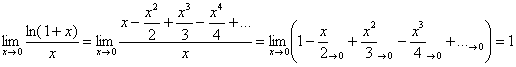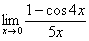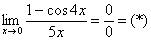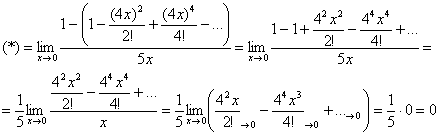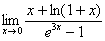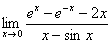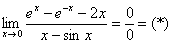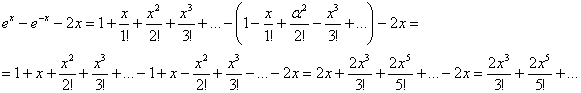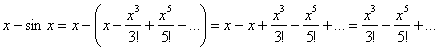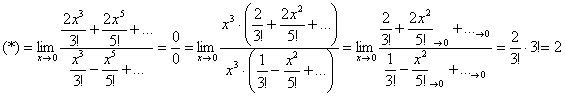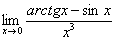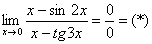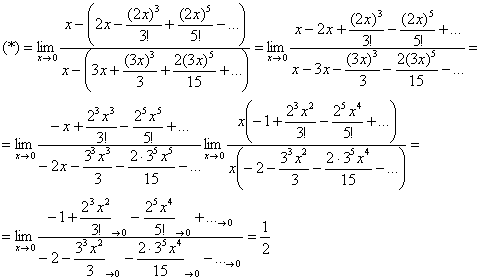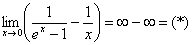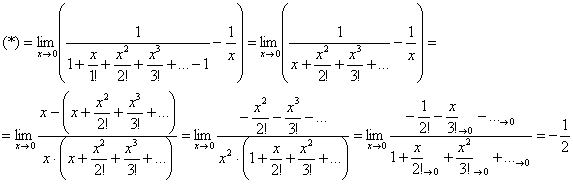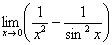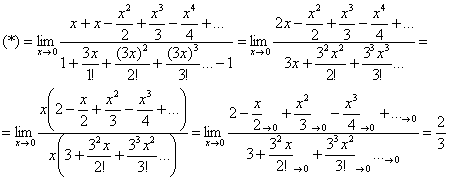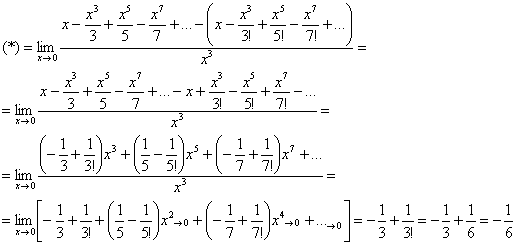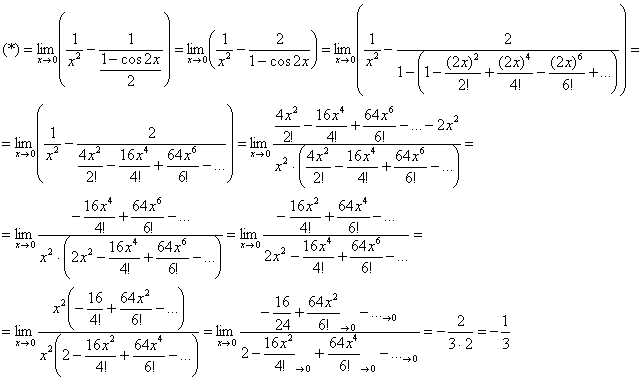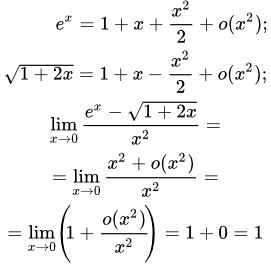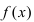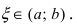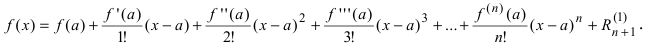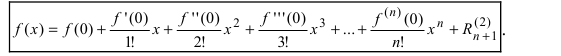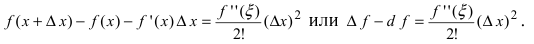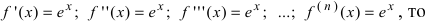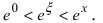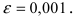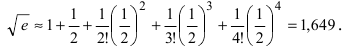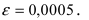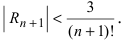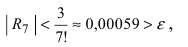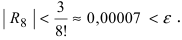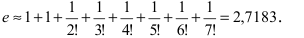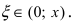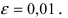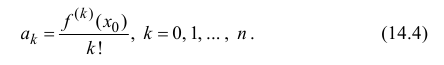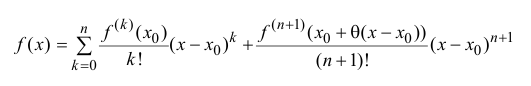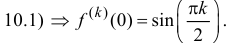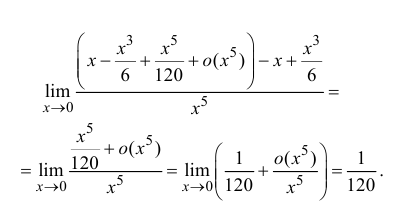Ряд тейлора как решать

Как вычислить предел функции с помощью ряда?

Этот коротенький урок посвящён ещё одному приложению степенных рядов, название которого вы видите в заголовке. Для решения примеров нам опять потребуется таблица разложений (откройте на соседней вкладке или распечатайте), и я предлагаю вам улучшить своё настроение! Потому что задание будет простое, приятное и его краткая суть такова: в некоторых пределах для устранения неопределённости оказывается эффективной замена функции(й) степенными рядами. Когда слова излишни:

И сразу обратите внимание на одну важную особенность: многие приложения степенных рядов посвящены приближённым вычислениям, однако в данном случае мы имеем дело с точным методом – поскольку меняем функцию на ВЕСЬ ряд. Если вам всё же не понятна суть этого действия, то, пожалуйста, обратитесь к статье о разложении функций.

Аналогичным способом можно доказать некоторые другие замечательные пределы:

Задание: используя таблицу разложений, проверьте, что 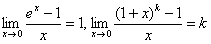. Задание, в общем-то, устное.

Очевидно, что предельное значение «икс» должно обязательно лежать в интервале сходимости ряда, и теоретически это может быть любое число данного интервала. Но практически оно, как правило, равно нулю, что избавляет нас от проблем с «хвостом» ряда.

Вычислить предел с помощью разложения функции в ряд

Это предел из Примера 4 статьи Замечательный пределы.

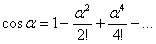
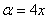
Используем разложение – много членов записывать не нужно, обычно хватает трёх-четырёх. В данном случае :

Не забываем проставлять троеточия и указывать, что остаток ряда стремится к нулю!

Вычислить предел с помощью степенных рядов

Краткое решение в конце урока. Сверьтесь с Примером 6 урока Правила Лопиталя.

И особо интересный предел (см. Пример 4 того же урока), в котором мы использовали правило Лопиталя дважды:

Вычислить предел с помощью степенных рядов

Вполне возможно, кому-то такое решение придётся больше по вкусу:

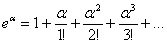
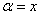
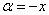
Используем разложение для и , и чтобы не запутаться, сразу упростим числитель:

Со знаменателем всё проще:

Рассматриваемый способ решения не является какой-то «проформой» и бывает действительно выгоден – когда в «начинке» предела находятся «разношёрстные» функции, особенно их суммы или разности:

Пользуясь известными разложениями функций в ряд Маклорена, вычислить следующий предел:

И даже в такой коротенькой статье не могу не порадовать вас новым и познавательным материалом!

Разложение тангенса в ряд Маклорена

, где – так называемые числа Бернулли. Данный ряд сходится при .

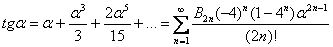
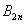
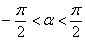
Вы спросите, почему разложения тангенса нет в таблице? Почти не требуется. ПризнАюсь, что данная «таблица» – это вообще не какая-то стандартная справка, а конспект, составленный на основе своего личного опыта. Так, например, во многих аналогичных «таблицах» вы не встретите разложения арктангенса и арксинуса (они выводятся – см. урок о сумме степенного ряда). Я же счёл нужным добавить их в pdf-ку, чтобы «далеко не ходить» – часто нужны на практике

Но вернёмся к теме:

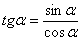
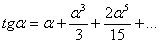
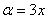
Да, конечно, здесь можно воспользоваться тригонометрической формулой , избавиться от трёхэтажности дроби и разобраться с двумя синусами и косинусом. Но к чему такие трудности? – если есть прямое разложение для :

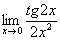
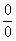
Ради шутки можете вычислить предел из Примера 3 урока Замечательные пределы. А кроме шуток, разложение функций в ряд используется для устранения не только неопределённости (как можно было бы подумать):

Вычислить предел с помощью степенного ряда

И при такой формулировке задания правила хорошего тона предписывают разложить экспоненту в ряд как можно скорее – ещё в знаменателе. Далее алгоритм работает стандартно: приводим выражение к общему знаменателю, после чего что-нибудь должно сократиться:

И заключительный предел для самостоятельного решения:

Вычислить предел, разложив функции в ряд Маклорена

Не знаете, что делать с квадратом синуса? Ай-яй-яй =)

Пример 2: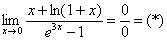
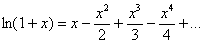
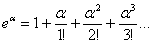
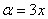
Используем ряд и разложение для :

Пример 4: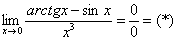
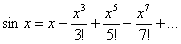
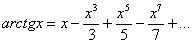
Используем разложения и :

Пример 7: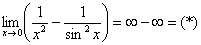
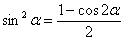
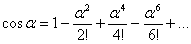
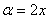
Используем тригонометрическую формулу и разложение для :

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

Решение пределов, используя ряд Тейлора

Метод решения

Этот метод применим, если после выполнения пункта 1), функции в числителе и знаменателе можно разложить в степенной ряд.

Применяемые свойства о малого

Определение и доказательство свойств о малого приводится на странице: «О большое и о малое. Сравнение функций». Здесь мы приводим свойства, используемые при решении пределов разложением в ряд Маклорена (то есть при ).

Разложение элементарных функций в ряд Тейлора (Маклорена)

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов с помощью ряда Тейлора.
⇓, ⇓, ⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Вычислить предел последовательности, используя разложение в ряд Тейлора.
.

Пример 2

Все примеры ⇑ Показать, что значение второго замечательного предела можно получить, используя разложение в ряд Тейлора.

Вычисляем предел в показателе, используя следующее разложение в ряд Тейлора:
.
.

Поскольку экспонента является непрерывной функцией для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 3

Все примеры ⇑ Вычислить предел, используя разложение в ряд Тейлора.
.

Раскладываем с точностью до квадратичных членов:
;
.
Делим числитель и знаменатель на и находим предел:
.

Пример 4

Все примеры ⇑ Решить предел с помощью ряда Тейлора.
.

Подставляем в исходную функцию.

.
Находим предел.
.

Пример 5

Все примеры ⇑ Найти предел с помощью ряда Тейлора.
.

Будем проводить разложение числителя и знаменателя в ряд Маклорена до четвертой степени включительно.

Подставляем разложение числителя и знаменателя и находим предел.
;
.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Источник

Формула Тейлора и ее применение с примерами решения

Содержание:

Формула Тейлора и ее применение

Формула Тейлора

Теорема: Если функция

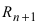
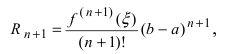
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора называется остаточным членом, вид которого установил Лагранж: величина

В этой формуле неизвестной является только величина 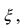причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид:

При a = 0 формула Тейлора переходит в формулу Маклoрена:

Пример:

Представить по формуле Маклорена функцию 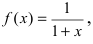ограничившись n=2.

Решение:

Вычислим три первых производных заданной функции:

При х = 0 получим Остаточный член имеет вид Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид: Отметим, что полученное выражение справедливо при Решим найденное равенство относительно величины Отсюда получаем Следовательно, Так как выражение под радикалом 4-ой степени должно быть неотрицательным и Таким образом, из двух корней теореме Тейлора удовлетворяет только корень который действительно лежит между нулем и х.

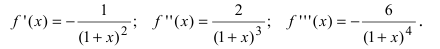
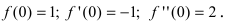
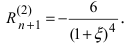
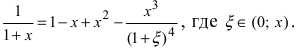
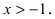
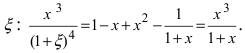
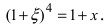
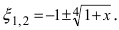
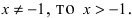
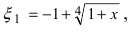
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:

(см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем Если положить то получим формулу

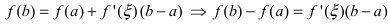
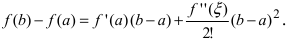
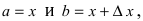
Применение формулы Тейлора

Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 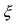в остаточном члене в форме Лагранжа лежит в пределах от а до х.

Пример:

Представить функцию 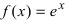по формуле Маклорена.

Решение:

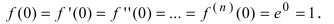
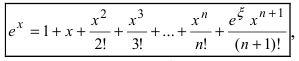
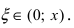
Так как Следовательно, где Отсюда следует,

Пример:

Вычислить 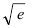с точностью

Решение:

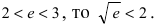
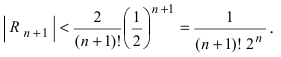
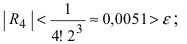
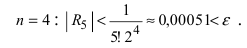
Так как основание Следовательно, при х = 1/2 остаточный член равен При n = 3: остаточный член Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что

Пример:

Вычислить число е с точностью

Решение:

Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа

При n = 6 имеем

при n = 7 получаем

Итак,

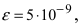
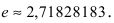
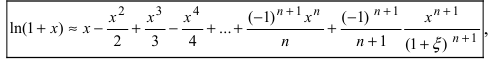
Если вычислять значение числа е с точностью то потребуется взять 13 первых слагаемых, при этом Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций. Например, для вычисления натуральных логарифмов используется формула:причем

Пример:

Вычислить 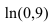с точностью

Решение:

Формула тейлора

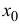
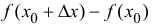
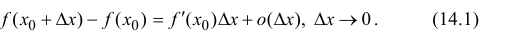
Пусть функция y=f(x) дифференцируема в точке . Тогда (см. формулу (9.5)) ее приращение

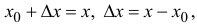
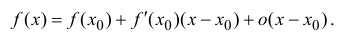
Пусть тогда (14.1) перепишется в виде
Рассмотрим многочлен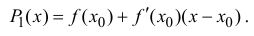
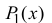
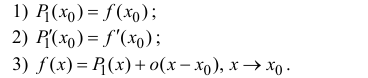
Многочлен обладает следующими свойствами:

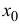
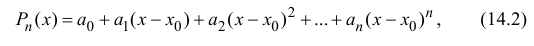
Пусть функция y=f(x) n раз дифференцируема в точке . Найдем многочлен

обладающий аналогичными свойствами: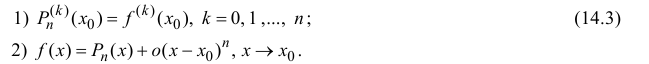

Из (14.2), (14.3) следует, что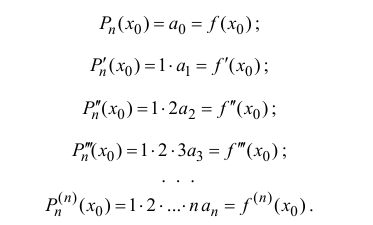

Поэтому коэффициенты 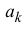многочлена (14.2) задаются формулой

Далее

Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 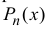задаются формулами (14.4)). Тем самым теорема доказана.
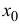
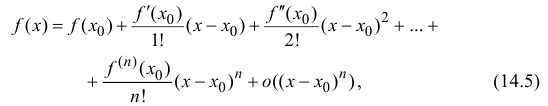
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке , тогда

где 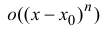– бесконечно малая функция более высокого порядка
малости, чем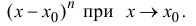
Формула (14.5) называется формулой Тейлора, многочлен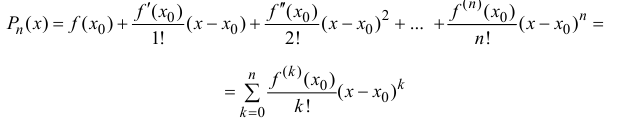

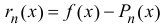
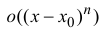
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности в виде – остаточным членом в форме Пеано.
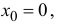
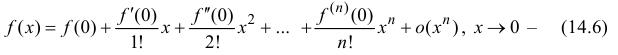
Если функция то (14.5) перепишется в виде

формула Маклорена.
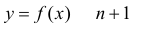
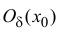
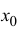
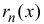
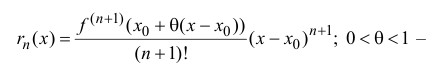
Если функция раз дифференцируема в некоторой окрестности
точки , то остаточный член можно представить в виде
остаточный член в форме Лагранжа и формула

называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.

Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений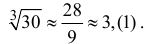
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа: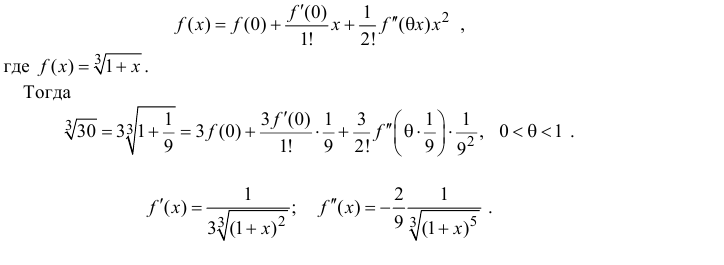

Поэтому

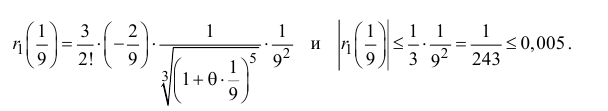
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.

Пример 14.2
Запишем формулу Маклорена n-го порядка для функции y=sin x: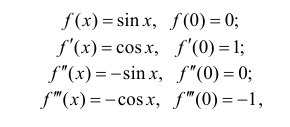

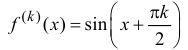
(см. упражнение 10.1)

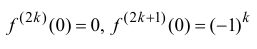
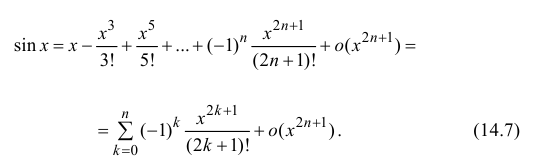
Таким образом, и по формуле (14.6)

Аналогично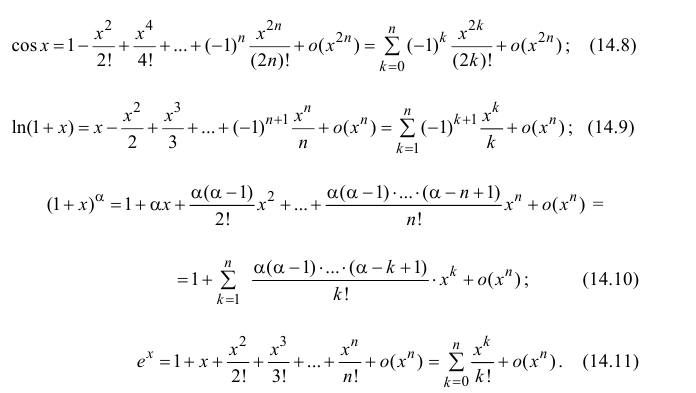

Формулы (14.7)–(14.11) называются основными разложениями.

Пример 14.3
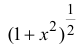
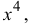
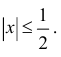
Разложить по формуле Маклорена до члена используя основные разложения. Оценить погрешность при
Решение
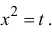
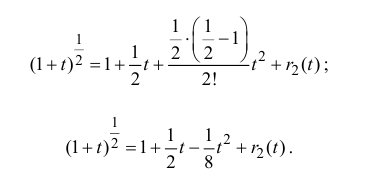
Пусть Тогда (см. формулу (14.10))

Остаточный член запишем в форме Лагранжа: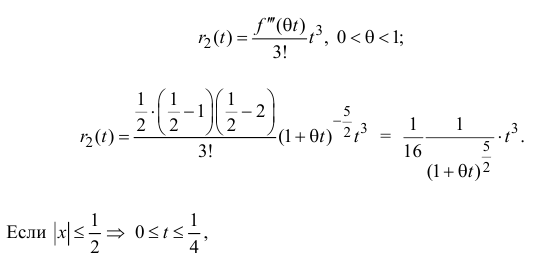

поэтому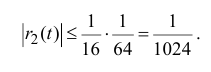
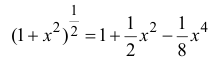
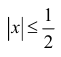
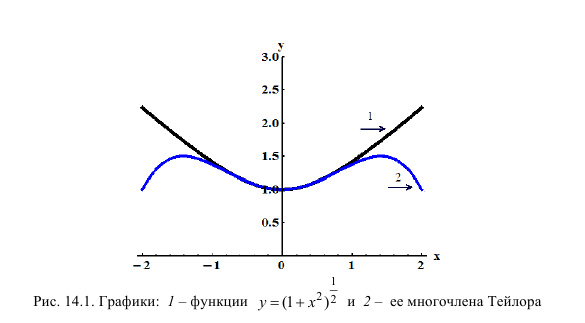
Таким образом, и погрешность при меньше чем

Пример 14.4
Найти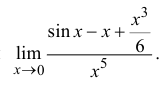
Решение
Воспользуемся разложением (14.7):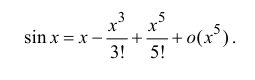

Тогда

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник