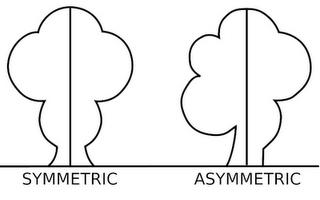
Симметричные фигуры это как

Что такое симметрия и асимметрия?

Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?

Что означает симметрия в разных науках?

Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.

Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.

Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.

Как определяют симметрию разные словари?

На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.

В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.

Когда говорят об асимметрии?

Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.

В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.

О центральной и осевой симметрии

В математике выделяют такие ее виды:

Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.

В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.

Какие фигуры являются симметричными?

Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.

Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.

Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.

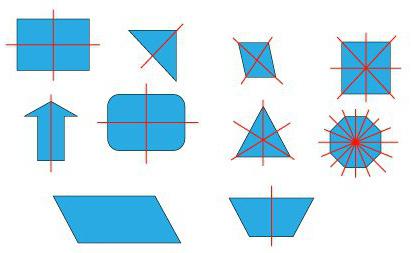
Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.

К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.

Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.

У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.

Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.

Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.

Источник

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

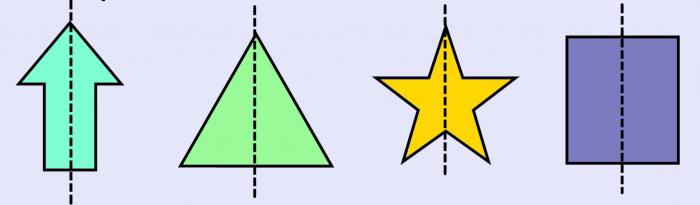
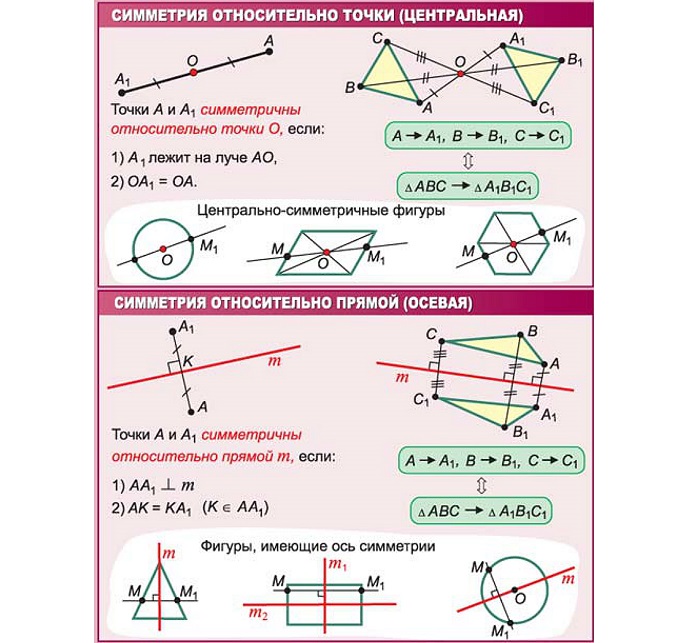
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

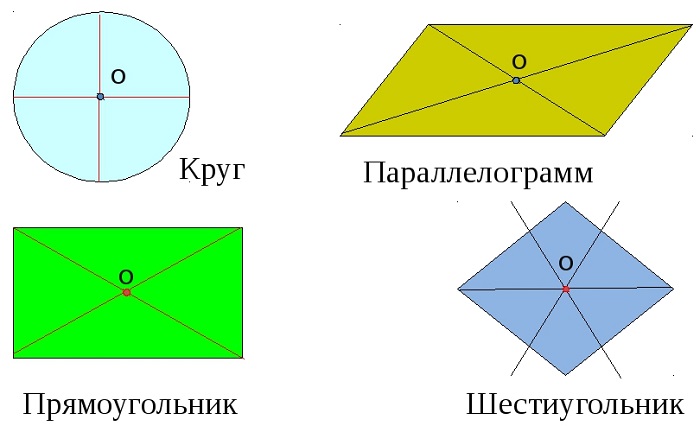
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Симметрия фигур в пространстве

Центральная симметрия

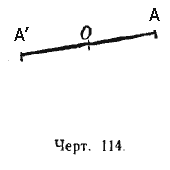
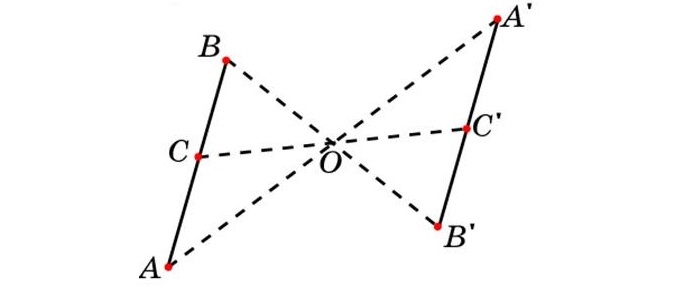
Две фигуры называются симметричными относительно какой-либо точки О пространства, если каждой точке А одной фигуры соответствует в другой фигуре точка А&#146, расположенная на прямой ОА по другую сторону от точки О, на расстоянии, равном расстоянию точки А от точки О (черт. 114). Точка О называется центром симметрии фигур.

Пример таких симметричных фигур в пространстве мы уже встречали (§ 53), когда, продолжая за вершину рёбра и грани многогранного угла, получали многогранный угол, симметричный данному. Соответственные отрезки и углы, входящие в состав двух симметричных фигур, равны между собой. Тем не менее фигуры в целом не могут быть названы равными: их нельзя совместить одну с другой вследствие того, что порядок расположения частей в одной фигуре иной, чем в другой, как это мы видели на примере симметричных многогранных углов.

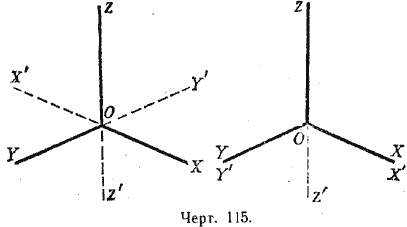
В отдельных случаях симметричные фигуры могут совмещаться, но при этом будут совпадать несоответственные их части. Например, возьмём прямой трёхгранный угол (черт. 115) с вершиной в точке О и рёбрами ОХ, OY, OZ.

Построим ему симметричный угол ОХ&#146Y&#146Z&#146. Угол OXYZ можно совместить с OX&#146Y&#146Z&#146 так, чтобы ребро ОХ совпало с OY&#146, а ребро OY c OX&#146. Если же совместить соответственные рёбра ОХ с ОХ&#146 и OY с OY&#146, то рёбра OZ и OZ&#146 окажутся направленными в противоположные стороны.

Правильный тетраэдр не имеет центра симметрии.

Симметрия относительно плоскости

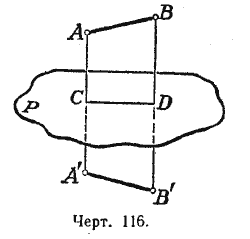
Две пространственные фигуры называются симметричными относительно плоскости Р, если каждой точке А в одной фигуре соответствует в другой точка А&#146, причём отрезок АА&#146 перпендикулярен к плоскости Р и в точке пересечения с этой плоскостью делится пополам.

Теорема. Всякие два соответственных отрезка в двух симметричных фигурах равны между собой.

Если какое-либо геометрическое тело можно разбить на две части, симметричные относительно некоторой плоскости, то эта плоскость называется плоскостью симметрии данного тела.

Геометрические тела, имеющие плоскость симметрии, чрезвычайно распространены в природе и в обыденной жизни. Тело человека и животного имеет плоскость симметрии, разделяющую его на правую и левую части.

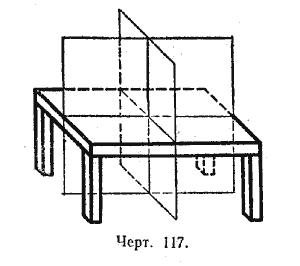
На этом примере особенно ясно видно, что симметричные фигуры нельзя совместить. Так, кисти правой и левой рук симметричны, но совместить их нельзя, что можно видеть хотя бы из того, что одна и та же перчатка не может подходить и к правой и к левой руке. Большое число предметов домашнего обихода имеет плоскость симметрии: стул, обеденный стол, книжный шкаф, диван и др. Некоторые, как например обеденный стол, имеют даже не одну, а две плоскости симметрии (черт. 117).

Обычно, рассматривая предмет, имеющий плоскость симметрии, мы стремимся занять по отношению к нему такое положение, чтобы плоскость симметрии нашего тела, или по крайней мере нашей головы, совпала с плоскостью симметрии самого предмета. В этом случае симметричная форма предмета становится особенно заметной.

Симметрия относительно оси. Ось симметрии второго порядка.

Из этого определения непосредственно следует, что если два геометрических тела, симметричных относительно какой-либо оси, пересечь плоскостью, перпендикулярной к этой оси, то в сечении получатся две плоские фигуры, симметричные относительно точки пересечения плоскости с осью симметрии тел.

Отсюда далее легко вывести, что два тела, симметричных относительно оси, можно совместить одно с другим, вращая одно из них на 180° вокруг оси симметрии. В самом деле, вообразим все возможные плоскости, перпендикулярные к оси симметрии.

Каждая такая плоскость, пересекающая оба тела, содержит фигуры, симметричные относительно точки встречи плоскости с осью симметрии тел. Если заставить скользить секущую плоскость саму по себе, вращая её вокруг оси симметрии тела на 180°, то первая фигура совпадает со второй.

Это справедливо для любой секущей плоскости. Вращение же всех сечений тела на 180° равносильно повороту всего тела на 180° вокруг оси симметрии. Отсюда и вытекает справедливость нашего утверждения.

Если после вращения пространственной фигуры вокруг некоторой прямой на 180° она совпадает сама с собой, то говорят, что фигура имеет эту прямую своею осью симметрии второго порядка.

Название «ось симметрии второго порядка » объясняется тем, что при полном обороте вокруг этой оси тело будет в процессе вращения дважды принимать положение, совпадающее с исходным (считая и исходное). Примерами геометрических тел, имеющих ось симметрии второго порядка, могут служить:

1) правильная пирамида с чётным числом боковых граней; осью её симметрии служит её высота;

2) прямоугольный параллелепипед; он имеет три оси симметрии: прямые, соединяющие центры его противоположных граней;

3) правильная призма с чётным числом боковых граней. Осью её симметрии служит каждая прямая, соединяющая центры любой пары её противоположных граней (боковых граней и двух оснований призмы). Если число боковых граней призмы 2k, то число таких осей симметрии будет k + 1. Кроме того, осью симметрии для такой призмы служит каждая прямая, соединяющая середины её противоположных боковых рёбер. Таких осей симметрии призма имеет А.

Таким образом, правильная 2k-гранная призма имеет 2k+1 осей, симметрии.

Зависимость между различными видами симметрии в пространстве.

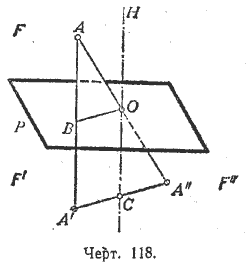
Теорема. Если фигура F симметрична с фигурой F&#146 относительно плоскости Р и в то же время симметрична с фигурой F» относительно точки О, лежащей в плоскости Р, то фигуры F&#146 и F» симметричны относительно оси, проходящей через точку О и перпендикулярной к плоскости Р.

Возьмём какую-нибудь точку А фигуры F (черт. 118). Ей соответствует точка А&#146 фигуры F&#146 и точка А» фигуры F» (сами фигуры F, F&#146 и F» на чертеже не изображены).

Оси симметрии высших порядков

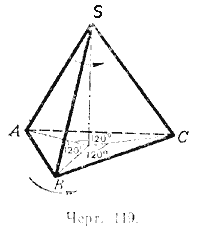
Фигура, имеющая ось симметрии, совмещается сама с собой после поворота вокруг оси симметрии на угол в 180°. Но возможны случаи, когда фигура приходит к совмещению с исходным положением после поворота вокруг некоторой оси на угол, меньший 180°. Таким образом, если тело сделает полный оборот вокруг этой оси, то в процессе вращения оно несколько раз совместится со своим первоначальным положением. Такая ось вращения называется осью симметрии высшего порядка, причём число положений тела, совпадающих с первоначальным, называется порядком оси симметрии. Эта ось может и не совпадать с осью симметрии второго порядка. Так, правильная треугольная пирамида не имеет оси симметрии второго порядка, но её высота служит для неё осью симметрии третьего порядка. В самом деле, после поворота этой пирамиды вокруг высоты на угол в 120° она совмещается сама с собой (черт. 119).

При вращении пирамиды вокруг высоты она может занимать три положения, совпадающие с исходным, считая и исходное. Легко заметить, что всякая ось симметрии чётного порядка есть в то же время ось симметрии второго порядка.

Примеры осей симметрии высших порядков:

1) Правильная n-угольная пирамида имеет ось симметрии n-го порядка. Этой осью служит высота пирамиды.

2) Правильная n-угольная призма имеет ось симметрии n-го порядка. Этой осью служит прямая, соединяющая центры оснований призмы.

Симметрия куба.

Куб имеет девять плоскостей симметрии: шесть диагональных плоскостей и три плоскости, проходящие через середины каждой четвёрки его параллельных рёбер.

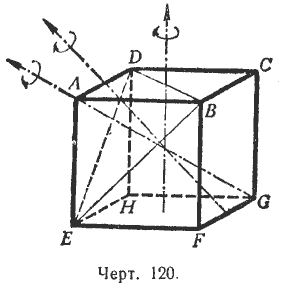
Куб имеет девять осей симметрии второго порядка: шесть прямых, соединяющих середины его противоположных рёбер, и три прямые, соединяющие центры противоположных граней (черт. 120).

Эти последние прямые являются осями симметрии четвёртого порядка. Кроме того, куб имеет четыре оси симметрии третьего порядка, которые являются его диагоналями. В самом деле, диагональ куба АG (черт. 120), очевидно, одинаково наклонена к рeбрам АВ, АD и АЕ, а эти рёбра одинаково наклонены одно к другому. Ecли соединить точки В, D и Е, то получим правильную треугольную пирамиду АDВЕ, для которой диагональ куба AG служит высотой. Когда при вращении вокруг высоты эта пирамида будет совмещаться сама с собой, весь куб будет совмещаться со своим исходным положением. Других осей симметрии, как нетрудно убедиться, куб не имеет. Посмотрим, сколькими различными способами куб может быть совмещён сам с собой. Вращение вокруг обыкновенной оси симметрии даёт одно положение куба, отличное от исходного, при котором куб в целом совмещается сам с собой.

Легко убедиться непосредственно, что все эти положения отличны одно от другого, а также и от исходного положения куба. Вместе с исходным положением они составляют 24 способа совмещения куба с самим собой.

Источник

СИММЕТРИЯ

Не все уравновешенные или сбалансированные фотографии симметричны – все симметричные композиции по умолчанию находятся в равновесии.

В фотографии наиболее часто используются три вида симметрии:

Фото: Hesham Alhumaid

Фото: Bildwerker Freidburg

Фото: Victor Mozqueda

Фото: Markus Studtmann

Фото: Hans Wolfgang Hawerkamp

Фото: Massimo Cuomo

АСИММЕТРИЯ

Асимметричное равновесие достигается тогда, когда элементы композиции, находящиеся по разные стороны от центра, имеют одинаковую визуальную массу. Достичь равновесия при помощи асимметрии сложнее, чем в симметричной композиции, так как между композиционными элементами более сложные пространственные отношения. Асимметричное равновесие более динамичное и интересное для привлечения внимания, чем симметричное.

Фото: Josef Sieberer

Фото: Uros Podlogar

Применяя знания на практике, вы можете совмещать симметрию с асимметрией и добиваться прекрасных результатов и привлекать больше внимания. Вот несколько примеров:

Фото: Stefan Neuweger

Фото: Karthi KN Raveendiran

Фото: Christian Muller

Фото: Jacqueline Hammer

Фото: Jacqueline Hammer

Фото: Knut Borge Strom

Сталкивая симметрию с асимметрией, необходимо помнить, что:

Симметрия и асимметрия окружают нас каждое мгновение в повседневной жизни, понятие данных терминов позволяет более осознанно и гармонично наблюдать за красотой окружающего мира и позволяет создавать неповторимые фотографии!

Читайте ещё о композиции в других наших статьях:

Источник

Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.

Что такое центральная симметрия

Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.

Свойства центральной симметрии

Основные свойства следующие:

1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.

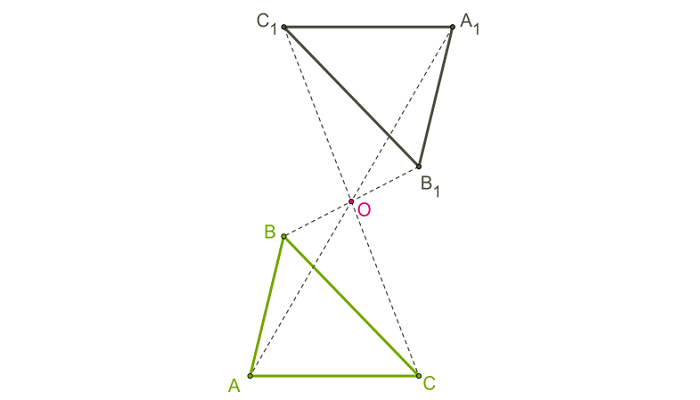
Посмотрим на рисунок. Треугольники АВС и А₁В₁С₁ симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А₁О, ВО=В₁О, СО=С₁О. Значит, картинка остаётся той же.

Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;

2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;

3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;

4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.

Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А₁В₁ относительно точки О_.

Далее соединяем симметричные точки и получаем отрезки АА₁ и ВВ₁. Далее легко заметить, что отрезки АО и А₁О будут равны. Соответственно равны и отрезки ВО и В₁О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.

Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А₁ и В,В_1. Значит они являются накрест лежащими при секущих АА₁ и ВВ₁. Задача решена, АВ и А₁В₁ параллельны;

5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.

Примеры фигур, обладающих центральной симметрией

Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:

различные правильные многоугольники.

Интересные факты о центральной симметрии

Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.

Ещё один очевидный пример – бабочка.

Великолепные узоры на её крылышках – четкая и яркая симметрия.

Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.

Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.

Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.

Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.

Источник