Склонение светила как определить

Экваториальная система небесных координат в навигации

Принципы экваториальной системы небесных координат и примеры навигационных расчетов.

В отличие от горизонтальной системы небесных координат, где за основную плоскость принят истинный горизонт небесной сферы, в экваториальной системе небесных координат основной плоскостью является плоскость небесного экватора, а полюсами являются полюсы мира. Положение светила в этой системе координат определяется склонением и часовым углом светила.

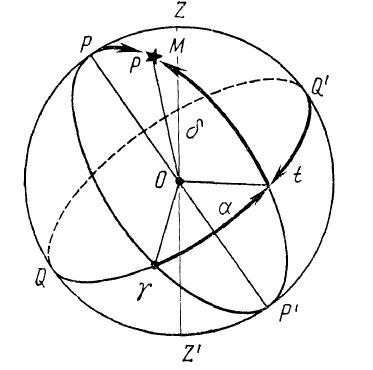
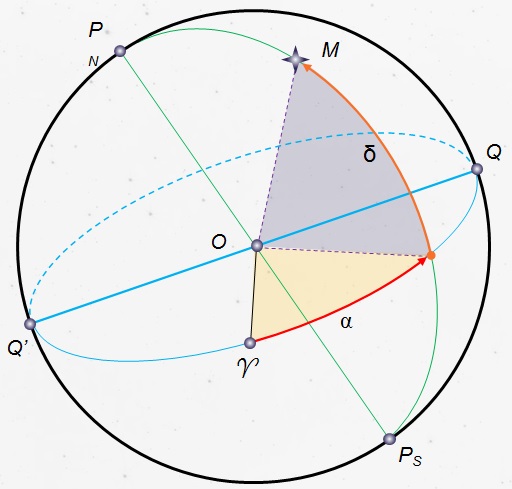
Общая схема принципа действия экваториальной системы небесных координат

Принцип экваториальной системы небесных координат

Склонением светила δ называется угол, заключенный между плоскостью небесного экватора и направлением на светило из центра небесной сферы. Склонение светила измеряется от 0 до ±90°.
Положительное склонение отсчитывается в направлении к Северному полюсу мира, а отрицательное — к Южному. Склонение Солнца, Луны и планет обычно берется из авиационного астрономического ежегодника для каждого часа гринвичского времени, а навигационных звезд — в таблице экваториальных координат звезд на начало каждого года ввиду изменения его за год на 1—2 градуса. Иногда вместо склонения светила пользуются другой координатой — полярным расстоянием.

Полярным расстоянием Р называется угол в плоскости круга склонения, заключенный между осью мира и направлением на светило из центра небесной сферы. Полярное расстояние отсчитывается от Северного полюса мира к Южному от 0 до 180°. Между полярным расстоянием и склонением светила имеется следующая зависимость:

Р + δ = 90°, откуда Р = 90° — δ; δ = 90° — Р

Светила, находящиеся на одной суточной параллели, имеют одинаковые склонения и одинаковые полярные расстояния. Склонение, или полярное расстояние, определяет положение светила на круге склонения. Положение же самого круга склонения на небесной сфере определяется часовым углом светила.

Часовым углом светила t называется двугранный угол в плоскости небесного экватора, заключенный между плоскостью небесного меридиана и плоскостью круга склонения светила.
Часовой угол отсчитывается от южного направления небесного меридиана по ходу часовой стрелки (к западу) до круга склонения светила от 0 до 360°. Важно знать, что отсчет часового угла светила ведется в направлении суточного вращения небесной сферы.

При решении некоторых задач для удобства часовые углы светил отсчитывают от 0 до 180° к западу и востоку и соответственно обозначают их t3 и tB. В Авиационном астрономическом ежегоднике даны западные часовые углы светил от 0 до 360°, а в расчетных таблицах для Солнца, Луны и планет — от 0 до 180°.

Важное значение имеет зависимость между часовым углом светила и долготой места наблюдателя. Выше указывалось, что часовой угол светила принято отсчитывать к западу от небесного меридиана. Так как плоскость небесного меридиана совпадает с географическим меридианом наблюдателя, то в один и тот же момент времени часовые углы одного и того же светила для наблюдателей, находящихся на разных меридианах, будут различны.
Очевидно, что в один и тот же момент времени разность местных часовых углов светила равна разности долгот наблюдателей t2-t1=λ2-λ1. Если принять в данном соотношении λ1=0, то t1 = tгр. Принимая λ1=λ и t2=t, получаем t=tгр+-λ b ₃.

Как видно из полученной формулы, местный часовой угол светила отличается от гринвичского на значение долготы наблюдателя. В практике часто вместо часового угла светила пользуются другой координатой — прямым восхождением светила.

Прямым восхождением светила α называется угол, заключенный между плоскостью круга склонения точки весеннего равноденствия (начального круга склонения) и плоскостью круга склонения светила.

Точкой весеннего равноденствия называется точка пересечения плоскости небесного экватора центром Солнца (21 марта) при его видимом годовом движении по небесной сфере. Эту точку принято обозначать символом созвездия Овен, в котором она находилась в эпоху зарождения астрономии.

Прямое восхождение светила отсчитывается в плоскости небесного экватора от точки весеннего равноденствия против хода часовой стрелки (к востоку) до круга склонения светила от 0 до 360°. Прямое восхождение светила и его часовой угол можно измерять не только углом, но и дугой небесного экватора, а склонение и полярное расстояние светила — дугой круга склонения.

Особенности экваториальной системы небесных координат

В авиационной астрономии экваториальная система небесных координат дополнительно подразделяется на две системы.

В первой экваториальной системе положение светила на небесной сфере определяется склонением и часовым углом, а во второй — прямым восхождением и склонением светила. Первая экваториальная система берется в основу при разработке и создании астрономических компасов, а также при составлении расчетных таблиц. Вторую экваториальную систему используют для составления звездных карт и таблиц экваториальных координат звезд.

Экваториальная система небесных координат является более практичной по сравнению с горизонтальной. Она имеет большое практическое значение в авиационной астрономии. С этой системой связано измерение времени и определение места самолета, т. е. решение главных вопросов практической авиационной астрономии.

Основным ее достоинством является то, что экваториальные координаты светил не зависят от места наблюдателя на земной поверхности, за исключением местного часового угла. Часовой угол светила зависит не только от долготы места наблюдателя, но и от времени наблюдения. Он непрерывно изменяется пропорционально времени, и это позволяет учитывать в астрокомпасах при помощи часового механизма его изменение за счет вращения Земли.

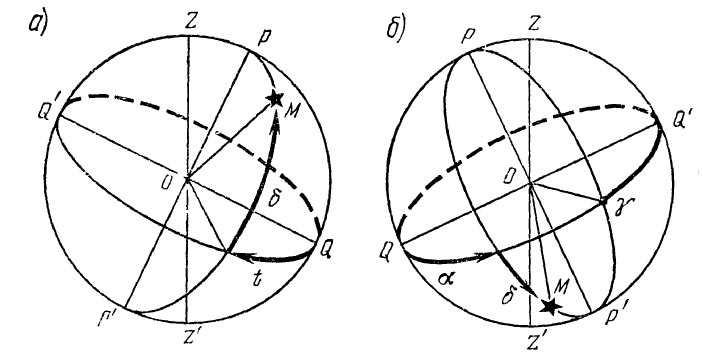
Ниже приведены примеры графического изображения положения светил на небесной сфере по заданным экваториальным координатам.

Иллюстрация принципа определения координат объекта с помощью экваториальной системы небесных координат (к примерам выше)

источник: по книге “Авиационная астрономия”

Источник

Склонение (астрономия)

Из Википедии — свободной энциклопедии

Склонение обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу от него, и находится в пределах от −90° до +90° включительно. У склонения принято указывать знак, даже если оно положительно.

Иногда склонение заменяется полярным расстоянием p = 90 ∘ − δ <\displaystyle p=90^<\circ >-\delta > , которое меняется в пределах от 0 до +180° и равно расстоянию до северного полюса мира.

Склонение связано с высотами верхней и нижней кульминации через широту φ (в этом случае южная широта считается отрицательной) [2] :

причём, если величина под модулем больше нуля — верхняя кульминация происходит к югу от зенита, а если меньше — к северу. Если широта места наблюдения равна склонению светила — высота равна 90 градусам и происходит в зените.

причём, если величина под модулем больше нуля — нижняя кульминация проходит к северу от надира, а если меньше — к югу. Если сумма широты и склонения равна нулю, то нижняя кульминация происходит в надире.

Тем не менее, восходящие и заходящие светила видно только в определённое для каждого из них время года: в зависимости от положения Солнца, оно может быть над горизонтом тогда же, когда и светило.

Источник

Практическая работа с подвижной картой звездного неба

Урок 10.

— Без данной программы можно выполнить работу с помощью подвижной карты звёздного неба: карта и накладной круг.

Практическая работа с подвижной картой
звездного неба.

Тема. Видимое движение Солнца

Учащиеся должны уметь:

1. Определять по карте экваториальные координаты светил и, наоборот, зная координаты находить светило и определять его название по таблице;

2. Зная экваториальные координаты Солнца, определять его положение на небесной сфере;

3. Определять время восхода и захода, а также время пребывания над горизонтом звезд и Солнца;

4. Вычислять высоту светила над горизонтом в верхней кульминации, зная географическую широту места наблюдения и определив его экваториальные координаты по карте; решать обратную задачу.

5. Определять склонения светил, которые не восходят или не заходят для данной широты места наблюдения.

Основные понятия. Экваториальная и горизонтальная система координат.

Демонстрационный материал. Подвижная карта звездного неба. Планетарий. Иллюстрации.

Самостоятельная деятельность учащихся. Выполнение заданий с помощью электронного планетария и подвижной карты звездного неба.

Мировоззренческий аспект урока. Формирование научного подхода к изучению мира.

Использование новых информационных технологий. Работа с интерактивным электронным планетарием.

1. На основе какой системы координат составляются звездные карты?

2. Назовите основную плоскость и точку отсчета в экваториальной системе координат. Найдите экватор и точку весеннего равноденствия на карте.

3. Где на карте находится северный полюс мира? (В центре).

4. Что называется склонением светила? Назовите единицы измерения.

5. Что показывает знак склонения?

6. Чему равно склонение точек, лежащих на экваторе?

Найдите на карте концентрические окружности, центр которых совпадает с северным полюсом мира. Эти окружности – параллели, т. е. геометрическое место точек, имеющих одинаковое склонение. Первая окружность от экватора имеет склонение 30°, вторая – 60°. Склонение отсчитывается от небесного экватора, если к северному полюсу, то δ > 0; если к югу от экватора, то δ

Источник

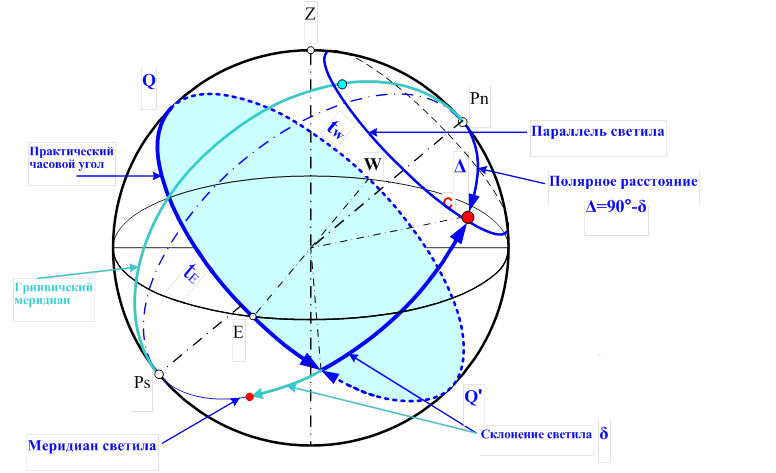
Первая экваториальная система координат

Первая экваториальная система координат светил ориентирована в пространстве относительно оси Мира (P_NOP_S).

В этой системе за основу берутся следующие плоскости:

Положение светила (С) на сфере относительно плоскости небесного меридиана наблюдателя и плоскости небесного экватора определяют две координаты:

Склонение светила, как и географическая широта, имеет северное (N) или южное (S) наименование.

Если светило расположено в южной (зюйдовой) половине сферы, то его склонению присваивается наименование южное (зюйдовое) и обозначается δ_S.

При решении задач, склонению светила одного наименования с широтой наблюдателя присваивается знак «плюс», а при противоположных наименованиях знак «минус».

На практике иногда пользуются не склонением светила, а его дополнением до 90°, т.е. дугой PnC, которое называется полярным расстоянием (Δ).

Полярное расстояние светилаΔ = 90° − δ измеряется дугой меридиана светила от повышенного полюса до видимого места светила в пределах от 0° до 180° и наименования не имеет.

Склонение светила (δ) показывает положение небесной параллели светила.

Если на одной небесной параллели одновременно находится несколько светил, то склонения этих светил будут иметь одинаковое значение.

Часовой угол светила (t) – это сферический угол при повышенном полюсе Мира между полуденной частью меридиана наблюдателя (принятого за начальный) и меридианом светила.

Часовой угол светила измеряется дугой небесного экватора от полуденной части меридиана наблюдателя (от т. Q) в сторону запада (т. W) до меридиана светила в пределах от 0° до 360°. Такая система счета часовых углов светил называется круговой (западной), а такой часовой угол светила называется обыкновенным или вестовым и обозначается t_W. Эта система соответствует суточному движению светил.

При решении ряда задач мореходной астрономии чаще всего используется практический часовой угол светила, который всегда меньше или равен 180° и измеряется дугой небесного экватора от полуденной части меридиана наблюдателя (начального) до меридиана светила в сторону запада (W) или востока (Е) в пределах от 0° до 180° (т.е. аналогично географической долготе). Практическому часовому углу светила присваивается наименование восточный (остовый) – t_E или западный (вестовый) – t_W в зависимости от того, в какую сторону он считается от полуденной части меридиана наблюдателя.

Если светило расположено на западной (вестовой) полусфере (t_W 180°) то остовый часовой угол светила рассчитывается по формуле: t_E =360° − t_W

В морском астрономическом ежегоднике (МАЕ) все часовые углы «вестовые» или «обыкновенные», хотя там их наименование и не указано.

Часовой угол, отсчитываемый от меридиана наблюдателя называется местным часовым углом светила t_M.

Часовой угол, отсчитываемый от Гринвичского (начального) меридиана, называется гринвичским часовым углом светила (t_ГР). Гринвичский и местный меридианы отстоят друг от друга на величину географической долготы λ, поэтому:

Часовой угол светила показывает положение небесного меридиана этого светила. Светила, расположенные одновременно на одной части небесного меридиана, имеют одинаковый часовой угол.

Часовой угол (t) и склонение (δ) светила не измеряются, а рассчитываются по МАЕ, для:

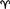
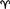
· точки Овна (только t_W т.к. δ = 0);

· Солнца;

· 4-х навигационных планет (Венера, Марс, Юпитер, Сатурн);

Источник

Как сказал.

Если вы студент, значит перед вами стоит тысяча возможностей. Найдите в себе силы, чтобы использовать хотя бы одну из них.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 04. Практическая работа № 1 «Изучение звёздного неба с помощью подвижной карты звёздного неба»

Практическая работа № 1

Тема: Изучение звёздного неба с помощью подвижной карты звёздного неба

Цель: познакомиться с подвижной картой звёздного неба,

научиться определять условия видимости созвездий

научиться определять координаты звезд по карте

Ход работы:

Теория.

Вид звёздного неба изменяется из-за суточного вращения Земли. Изменение вида звёздного неба в зависимости от времени года происходит вследствие обращения Земли вокруг Солнца. Работа посвящена знакомству со звёздным небом, решению задач на условия видимости созвездий и определении их координат.

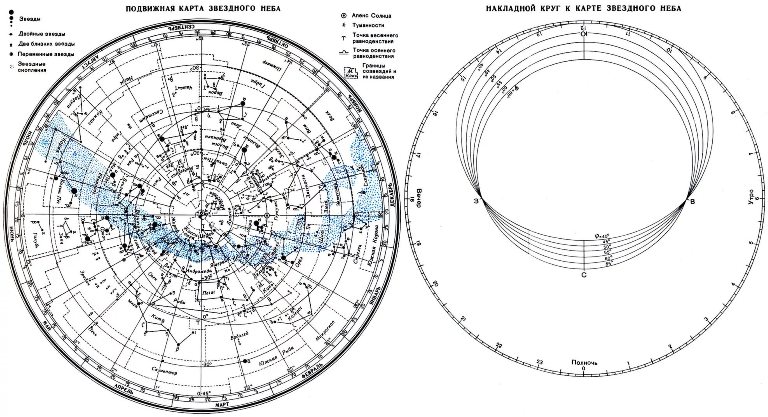
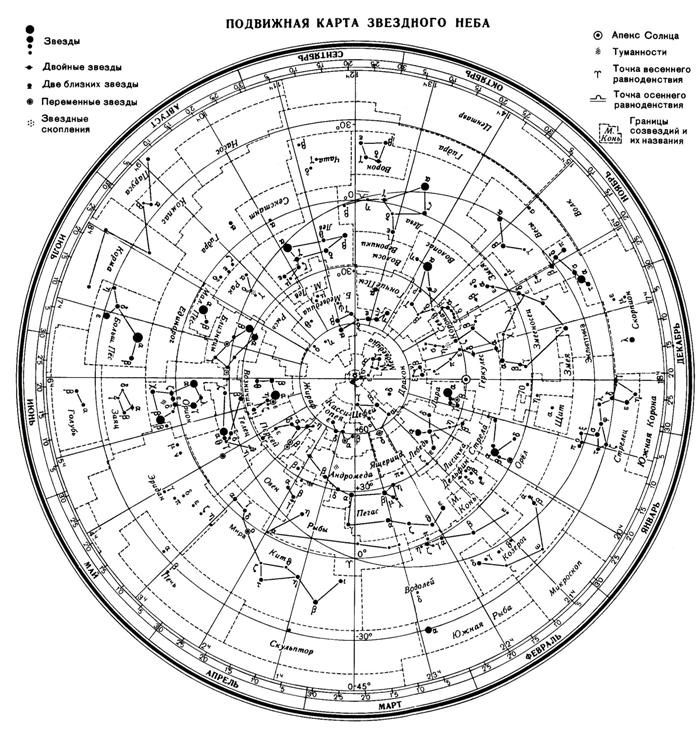
Подвижная карта звёздного неба изображена на рисунке.

Перед началом работы распечатать подвижную карту звездного неба, овал накладного круга вырезать по линии, соответствующей географической широте места наблюдения. Линия выреза накладного круга будет изображать линию горизонта. Звёздную карту и накладной круг наклеить на картон. От юга к северу накладного круга натянуть нить, которая покажет направление небесного меридиана.

Для определения местоположения небесного светила необходимо месяц, число, указанное на звёздной карте, совместить с часом наблюдения на накладном круге.

Небесный экватор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и совпадает с плоскостью земного экватора. Небесный экватор делит небесную сферу на два полушария: северное полушарие, с вершиной в северном полюсе мира, и южное полушарие, с вершиной в южном полюсе мира. Созвездия, через которые проходит небесный экватор, называют экваториальными. Различают созвездия южные и северные.

Созвездия Северного полушария: Большая и Малая Медведицы, Кассиопея, Цефей, Дракон, Лебедь, Лира, Волопас и др.

К южным относятся Южный Крест, Центавр, Муха, Жертвенник, Южный Треугольник.

Полюс мира — точка на небесной сфере, вокруг которой происходит видимое суточное движение звёзд из-за вращения Земли вокруг своей оси. Направление на Северный полюс мира совпадает с направлением на географический север, а на Южный полюс мира — с направлением на географический юг. Северный полюс мира находится в созвездии Малой Медведицы с поляриссимой (видимая яркая звезда, находящаяся на оси вращения Земли) — Полярной звездой, южный — в созвездии Октант.

Туманность — участок межзвёздной среды, выделяющийся своим излучением или поглощением излучения на общем фоне неба. Ранее туманностями называли всякий неподвижный на небе протяжённый объект. В 1920-е годы выяснилось, что среди туманностей много галактик (например, Туманность Андромеды). После этого термин «туманность» стал пониматься более узко, в указанном выше смысле. Туманности состоят из пыли, газа и плазмы.

Эклиптика — большой круг небесной сферы, по которому происходит видимое годичное движение Солнца. Плоскость эклиптики — плоскость обращения Земли вокруг Солнца (земной орбиты).

В зависимости от места наблюдателя на Земле меняется вид звездного неба и характер суточного движения звезд. Cуточные пути светил на небесной сфере — это окружности, плоскости которых параллельны небесному экватору.

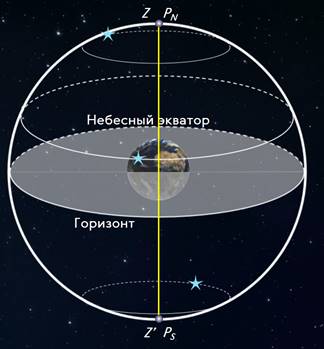
Рассмотрим, как изменяется вид звездного неба на полюсах Земли. Полюс — это такое место на земном шаре, где ось мира совпадает с отвесной линией, а небесный экватор — с горизонтом.

Для наблюдателя, находящегося на Северном полюсе Земли, Полярная звезда будет располагаться в зените, звёзды будут двигаться по кругам, параллельным математическому горизонту, который совпадает с небесным экватором. При этом над горизонтом будут видны все звёзды, склонение которых положительно (на Южном полюсе, наоборот, будут видны все звезды, склонение которых отрицательно), а их высота в течение суток не будет изменяться.

Переместимся в привычные для нас средние широты. Здесь уже ось мира и небесный экватор наклонены к горизонту. Поэтому и суточные пути звёзд также будут наклонены к горизонту. Следовательно, на средних широтах наблюдатель сможет наблюдать восходящие и заходящие звёзды.

Под восходом понимается явление пересечения светилом восточной части истинного горизонта, а под заходом — западной части этого горизонта.

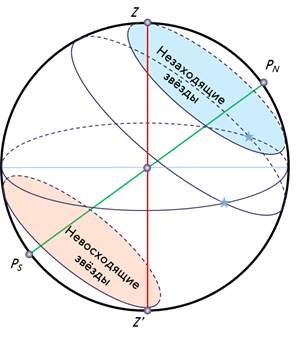
Помимо этого, часть звёзд, располагающихся в северных околополярных созвездиях, никогда не будут опускаться за горизонт. Такие звёзды принято называть незаходящими.

А звёзды, расположенные около Южного полюса мира для наблюдателя на средних широтах будут являться невосходящими.

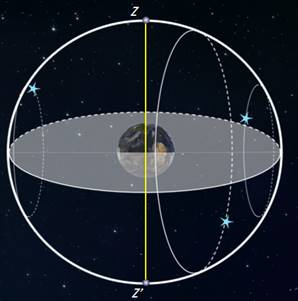
Отправимся дальше — на экватор, географическая широта которого равна нулю. Здесь ось мира совпадает с полуденной линией (то есть располагается в плоскости горизонта), а небесный экватор проходит через зенит.

Суточные пути всех, без исключения, звёзд перпендикулярны горизонту. Поэтому находясь на экваторе, наблюдатель сможет увидеть все звёзды, которые в течение суток восходят и заходят.

Вообще, для того, чтобы светило восходило и заходило, его склонение по абсолютной величине должно быть меньше, чем .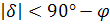

Если 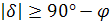, то в Северном полушарии она будет являться незаходящей (для Южного — невосходящей).

Тогда очевидно, что те светила, склонение которых 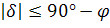, являются невосходящими для Северного полушария (или незаходящими для Южного).

Экваториальная система координат — это система небесных координат, основной плоскостью в которой является плоскость небесного экватора.

Экваториальные небесные координаты:

1. Склонение (δ) — угловое расстояние светила М от небесного экватора, измеренное вдоль круга склонения. Обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу от него. Объект на небесном экваторе имеет склонение 0°. Склонение северного полюса небесной сферы равно +90° Склонение южного полюса равно −90°.

2. Прямое восхождение светила (α) — угловое расстояние, измеренное вдоль небесного экватора, от точки весеннего равноденствия до точки пересечения небесного экватора с кругом склонения светила.

Последовательность выполнения практической работы:

Задачи практической работы:

Задача 1. Определите экваториальные координаты Альтаира (α Орла), Сириуса (α Большого Пса) и Веги (α Лиры).

Задача 2. Используя карту звёздного неба, найдите звезду по её координатам: δ = +35о; α = 1ч 6м.

Задача 3. Определите, какой является звезда δ Стрельца, для наблюдателя, находящего на широте 55о 15ʹ. Определить, восходящей или невосходящей является звезда двумя способами: с использованием накладного круга подвижной карты звездного неба и с использованием формул условия видимости звезд.

Практический способ. Располагаем подвижный круг на звездной карте и при его вращении определяем, является звезда восходящей или невосходящей.

Теоретичекий способ.

Используем формулы условия видимости звезд:

Если 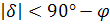, то звезда является восходящей и заходящей.

Если 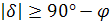, то звезда в Северном полушарии является незаходящей

Если 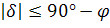, то звезда в Северном полушарии является невосходящей.

Задача 4. Установить подвижную карту звёздного неба на день и час наблюдения и назвать созвездия, расположенные в южной части неба от горизонта до полюса мира; на востоке – от горизонта до полюса мира.

Задача 5. Найти созвездия, расположенные между точками запада и севера, 10 октября в 21 час. Проверить правильность определения визуальным наблюдением звёздного неба.

Задача 6. Найти на звёздной карте созвездия с обозначенными в них туманностями и проверить, можно ли их наблюдать невооруженным глазом глазом на день и час выполнения лабораторной работы.

Задача 7. Определить, будут ли видны созвездия Девы, Рака. Весов в полночь 15 сентября? Какое созвездие в это же время будет находиться вблизи горизонта на севере?

Задача 9. На карте звёздного неба найти пять любых перечисленных созвездий: Большая Медведица, Малая Медведица, Кассиопея, Андромеда, Пегас, Лебедь, Лира, Геркулес, Северная корона – и определить приближённо небесные координаты (склонение, и прямое восхождение) a-звёзд этих созвездий.

Задача 10. Определить, какие созвездия будут находиться вблизи горизонта на Севере, Юге, Западе и Востоке 5 мая в полночь.

Контрольные вопросы для закрепления теоретического материала к практическому занятию:

3. Сколько на сегодняшний день созвездий? (Сегодня есть 88 созвездий. Созвездия различны по занимаемой площади на небесной сфере и количеству звезд в них.)

5. Что такое карта неба? ( Это изображение звёздного неба или его части на плоскости. Карту неба астрономы разделили на 2 части: южную и северную (по аналогии с полушариями Земли.)

6. Что такое небесный экватор? (Большой круг небесной сферы, плоскость которого перпендикулярна оси мира и совпадает с плоскостью земного экватора.)

По окончанию практической работы студент должен представить отчет.

Отчёт должен включать ответы на все указанные пункты порядка выполнения работы и ответы на контрольные вопросы.

Список литературы

1. Воронцов-Вельяминов Б. А., Страут Е. К. «Астрономия. 11 класс». Учебник с электронным приложением — М.: Дрофа, 2017

2. Р. А. Дондукова «Изучение звёздного неба с помощью подвижной карты» Руководство по проведению лабораторных работ М.: «Высшая школа» 2000

Источник