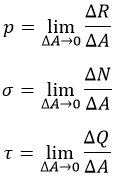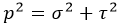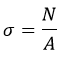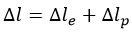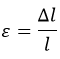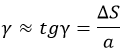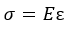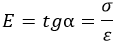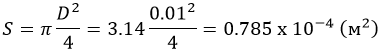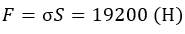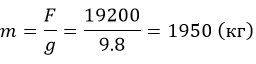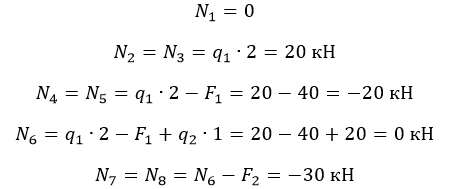Сопромат как решать задачи

21.09.202328.09.2023 admin 0 Comments

iSopromat.ru

Задачи с решениями по сопромату и технической механике с необходимыми пояснениями, графическими построениями и видеоуроками.

Задачи по условию

Наш короткий видеоурок по расчету реакций опор балки:

Примеры решения задач по расчету стержней, балок и валов на прочность.
Подбор сечений, проверка на прочность и определение грузоподъемности.

Примеры построения эпюр внутренних усилий, напряжений и перемещений при растяжении-сжатии, кручении, изгибе и других видах деформации.

Примеры расчетов нормальных, касательных и главных напряжений при различных видах деформации. Рассмотрены аналитические и графический способ (круг Мора) определения напряжений.

Примеры расчетов деформации бруса при различных видах нагружения.

Задачи по видам нагружения

Примеры решения задач и расчетно-графических работ по теме растяжение-сжатие стержней и стержневых систем.

Примеры решения задач и РГР на тему кручение валов.

Примеры решения задач и РГР по теме плоский поперечный изгиб балок.

Другие примеры решения задач по сопротивлению материалов представлены в нашей подборке:

Олимпиадные задачи

Примеры решения задач для олимпиад по сопротивлению материалов.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Техническая механика

Решение задач по сопромату

Примеры решения задач по сопротивлению материалов

Решение задачи на растяжение и сжатие

Построить эпюру напряжений в ступенчатом круглом брусе, нагруженном продольными силами и указать на наиболее напряженный участок.
Весом бруса пренебречь.

Решение задачи с использованием закона Гука

Определить величину растягивающей силы F , если известно, что под ее действием брус удлинился на величину ΔL .

Удлинение бруса ΔL = 0,005 мм;
Модуль продольной упругости балки Е = 2,0×10 5 МПа;
Площадь сечения бруса A = 0,01 м 2 ;
Размеры бруса и точка приложения силы F приведены на схеме.

Решить задачу можно, используя известную зависимость между линейными удлинениями и нагрузками (закон Гука).
Согласно закону Гука, представленному в расширенном виде:

Поскольку сила F приложена не к крайнему сечению бруса, а к его середине, то удлинился лишь участок между жесткой заделкой и сечением, к которому приложена растягивающая сила, имеющий длину L₁ = 2 м.
Учитывая это, определяем силу, вызвавшую удлинение бруса (не забываем привести все величины к единицам системы СИ):

Решение задачи на срез и смятие

Венец зубчатого колеса прикреплен к ступице болтовыми соединениями из шести болтов с гайками, размещенными равномерно по окружности диаметром D .
Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.

Номинальный крутящий момент на валу шестерни: Мкр = 10 Нм;
Диаметр окружности, на которой размещены болтовые соединения D = 0,4 м;
Диаметр стержня болта d = 10 мм.

Для решения задачи воспользуемся зависимостью между напряжением среза, внешней нагрузкой и площадью сечения по плоскости среза:

Решение задачи на срез и смятие шпонки

Произвести проверочный расчет призматической шпонки на смятие.

Вращающий момент на валу Т = 120 Нм;
Радиус сечения вала r = 30 мм;
Высота шпонки h = 6 мм;
Рабочая длина шпонки l_р = 30 мм;
Допускаемое напряжение на смятие [σ]_см = 200 МПа

Полученное напряжение сравниваем с допускаемым напряжением смятия [σ_см] = 200 МПа, и делаем вывод, что шпонка выдержит нагрузку.

Решение задачи на кручение

Построить эпюру вращающих моментов для круглого однородного бруса, представленного на схеме. Указать наиболее нагруженный участок бруса и определить напряжение в его сечениях.

Вращающие моменты:
Т₁ = 150 Нм;
Т₂ = 400 Нм;
Т₃ = 50 Нм;
Диаметр бруса d = 0,05 м.

Из эпюры очевидно, что максимальный крутящий момент возникает в сечениях участка I: Мкр = 500 Нм. Для определения напряжения (при кручении возникает касательное напряжение), воспользуемся зависимостью, полученной ранее:

τ_max ≈ М_кр / 0,2d 3 ≈ 500/0,2×0,05 3 ≈ 200 000 000 Па (или 200 МПа).

С правилами и примерами построения эпюр при деформации кручения можно ознакомиться здесь.

Решение задачи на изгиб

Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F .
Вес бруса не учитывать.

Исходные данные:

Поперечная сила F = 1000 Н;
Длина бруса L = 5 м;
Диаметр бруса d = 0,1 м.

Максимальные нормальные напряжения в этом сечении можно определить по формуле:

Решение задачи на изгиб с построением эпюр

Построить эпюру поперечных сил и изгибающих моментов, действующих на защемленный одним концом брус (см. схему).

Поперечная сила F = 50 Н;
Распределенная нагрузка q = 10 Н/м;
Длина бруса L = 12 м;
Вес бруса не учитывать.

Далее, используя метод сечений, строим эпюру поперечных сил, учитывая знаки. Очевидно, что на первом участке поперечная сила будет постоянной во всех сечениях, и эпюра представляет собой горизонтальную линию, отстоящую от оси эпюры на величину -F (сила отрицательная).

Источник

Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».

На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.

Что такое сопромат

Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.

Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.

Основные задачи по сопротивлению материалов

Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.

Требования

Перечислены далеко не все, но для статики и базовой программы хватит:

Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.

Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.

Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.

Материал и силы

Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:

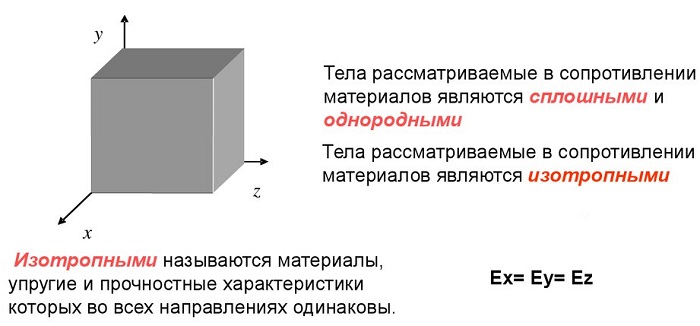
материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;

свойства не зависят от направления;

образец восстанавливает начальные параметры при снятии нагрузки;

поперечные сечения не меняются при деформации;

в удаленных от места нагрузки местах усилие распределяется равно по сечению;

результат воздействия нагрузок равен сумме последствий от каждой;

деформации не влияют на точки приложения сил;

отсутствуют изначальные внутренние напряжения.

Схемы

Служат для создания возможности расчета реальных конструкций:

тело – объект с практически одинаковыми «длина х ширина х высота»;

брус (балка, стержень, вал) – характеризуется значительной длиной.

На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):

Рис. 1. Опоры с воспринимаемыми реакциями:

в) жесткая заделка (защемление).

Силы в сопромате

Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».

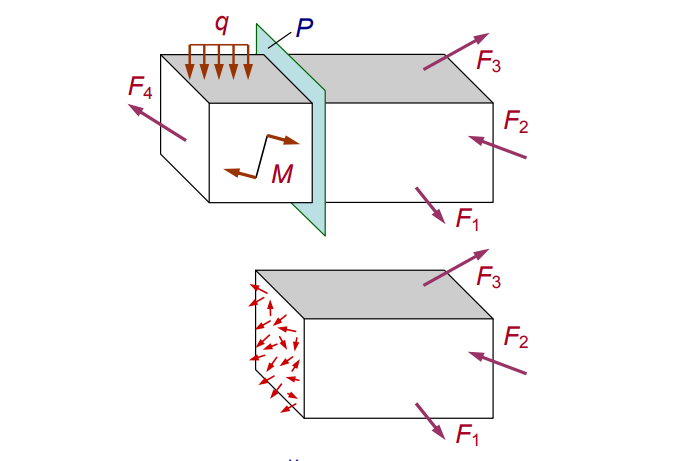
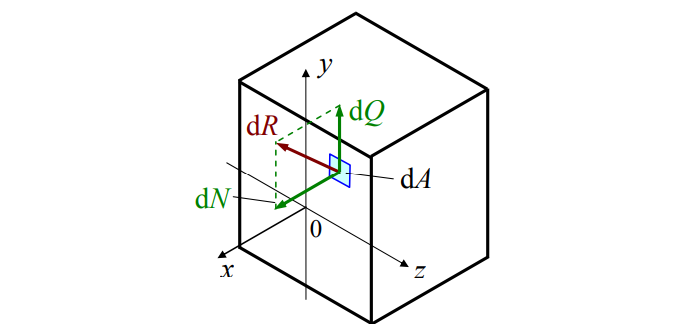
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).

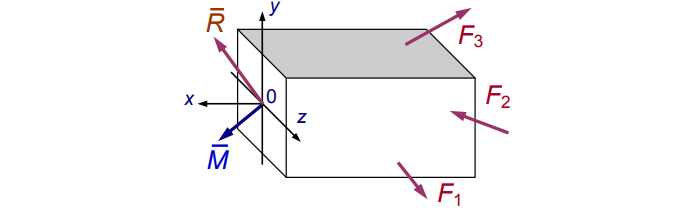
Заменим хаос равнодействующей R и моментом M (см. рис. 3):

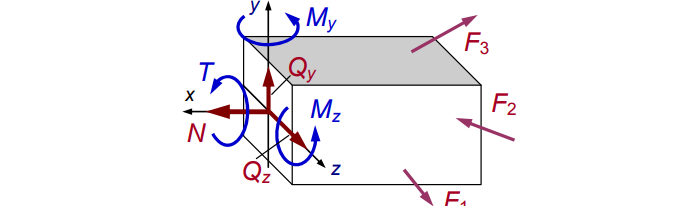
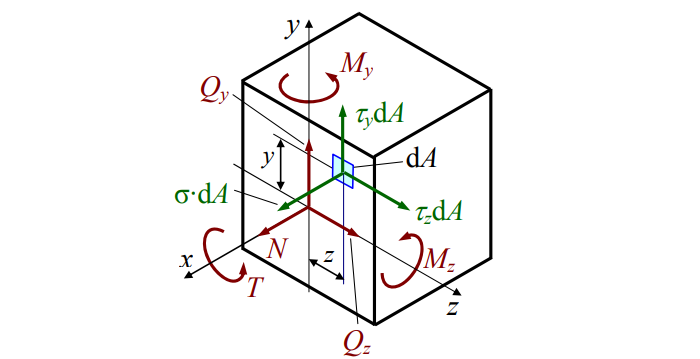
Распределив по осям, получим картину нагрузки сечения (см. рис. 4):

Нагрузки и деформации, изучаемые в сопромате

Изучим несколько принятых терминов.

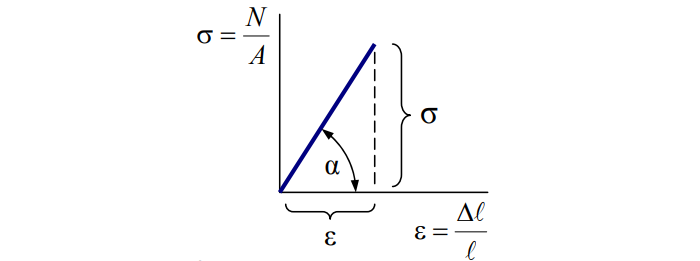
Напряжения

В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:

Элементарные усилия таковы:

σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;

τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;

p – полное напряжение.

Просуммировав элементы, получим:

N – нормальная сила;

A – площадь сечения.

В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).

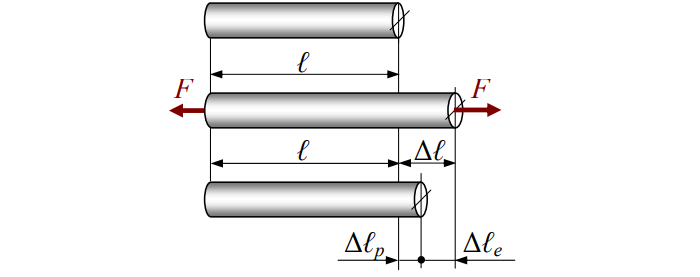
Деформации

Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.

Полная деформация будет равна:

Деформация относительная обозначается «ε» и рассчитывается так:

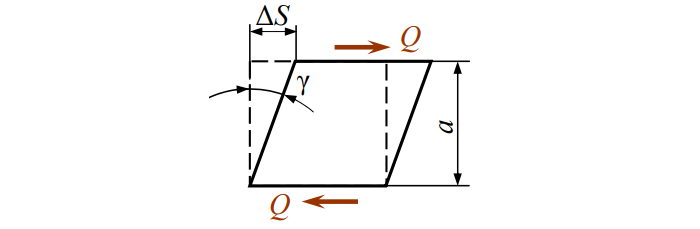
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:

Здесь γ – относительный сдвиг.

Виды нагрузки

Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).

Кручение – действует момент. Обычно рассчитываются передающие усилия валы.

Изгиб – воздействие направлено на искривление.

Основные формулы

Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:

E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 10 6 Па.

Сопротивление материала прямо пропорционально деформации:

Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.

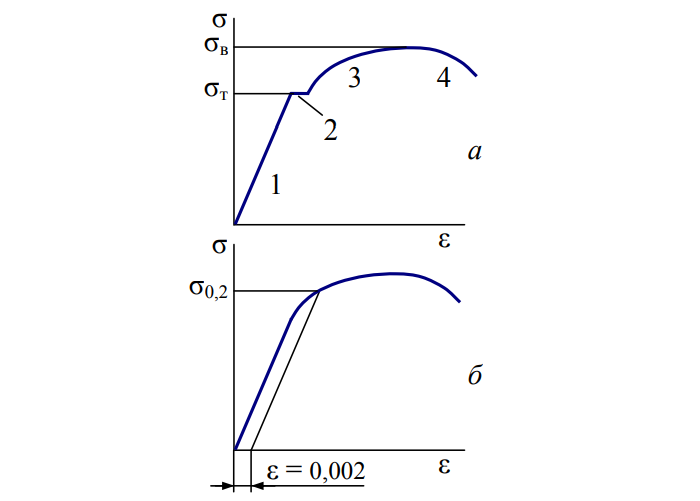
Реальная диаграмма

Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:

График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.

Расчеты обычно ведут по σ_т (а) и σ_0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.

Пример решения задачи

Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?

σ_0,2 для стали 45 равна 245 МПа (из ГОСТ).

Площадь сечения прутка:

Допустимая сила тяжести:

Для получения веса следует разделить на ускорение свободного падения g:

Ответ: необходимо подвесить груз массой 1950 кг.

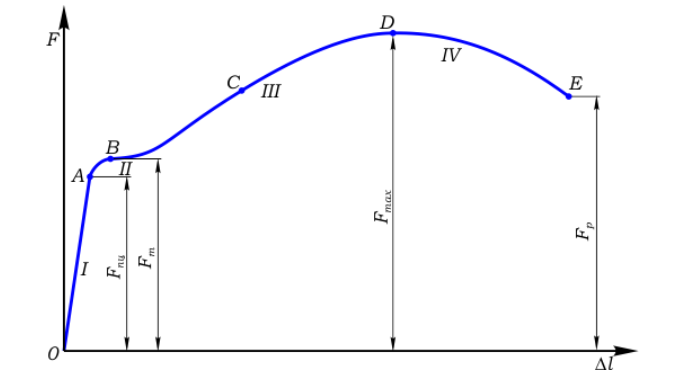
Как найти опасное сечение

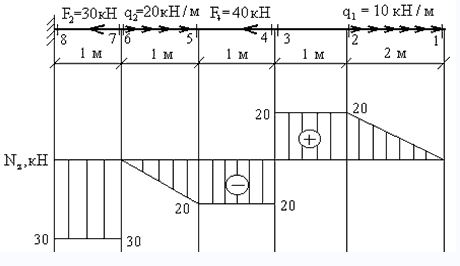
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.

Усилие положительно, если направлено на растяжение.

На схеме показано, что:

Зачем и кому нужен сопромат

Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.

Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».

Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Задачи на растяжение-сжатие

Расчет статически неопределимой стержневой системы

Задача. Определить напряжение в стальных стержнях, поддерживающих абсолютно жёсткую балку. Материал — сталь Ст3, α=60°, [σ]=160МПа.

В шарнирно-неподвижной опоре А возникают реакции R_А и Н_А. В стержнях 1 и 2 возникают усилия N₁ и N₂. Применим метод сечений. Замкнутым разрезом вырежем среднюю часть системы. Жесткую балку покажем схематично — линией, усилия N₁ и N₂ направим от сечения.

Составляем уравнения равновесия

Количество неизвестных превышает количество уравнений статики на 1. Значит, система один раз статически неопределима, и для её решения потребуется одно дополнительное уравнение. Чтобы составить дополнительное уравнение, следует рассмотреть схему деформации системы. Шарнирно-неподвижная опора А остается на месте, а стержни деформируются под действием силы.

Схема деформаций

По схеме деформаций составим условие совместности деформаций из рассмотрения подобия треугольников АСС₁ и АВВ₁. Из подобия треугольников АВВ₁ и АСС₁ запишем соотношение:

, где ВВ₁=Δℓ₁ (удлинение первого стержня)

Теперь выразим СС₁ через деформацию второго стержня. Укрупним фрагмент схемы.

Превратим условие совместности деформации (4) в уравнение совместности деформации с помощью формулы Гука для деформаций. При этом обязательно учитываем характер деформаций (укорочение записываем со знаком «-», удлинение со знаком «+»).

Тогда уравнение совместности деформаций будет:

Сокращаем обе части на Е, подставляем числовые значения и выражаем N₁ через N₂

Подставим соотношение (6) в уравнение (3), откуда найдем:

N₁ = 7,12кН (растянут),

Определим напряжения в стержнях.

Задача на статически неопределимый брус с зазором

Расчет бруса с зазором. Для статически неопределимого стального ступенчатого бруса построить эпюры продольных сил, нормальных напряжений, перемещений. Проверить прочность бруса. До нагружения между верхним концом и опорой имел место зазор Δ=0,1 мм. Материал – сталь Ст 3, модуль продольной упругости Е=2·10 5 МПа, допускаемое напряжение [σ]=160МПа.

В уравнении 2 неизвестных, а уравнение одно, значит задача 1 раз статически неопределима, и для ее решения требуется 1 дополнительное уравнение.

Это уравнение совместности деформаций. В данном случае совместность деформаций участков бруса состоит в том, что изменение длины бруса (удлинение) не может превзойти величины зазора, т.е. Δℓ=Δ, это условие совместности деформации.

Выпишем отдельно значения продольных сил в сечениях:

3. Вернемся к составлению условия совместности деформации. Имеем 4 участка, значит

Используя формулу Гука для определения абсолютной деформации составим уравнение совместности деформаций, — это именно то дополнительное уравнение, которое необходимо для решения задачи.

Е – модуль упругости, Е=2·10 5 МПа=2·10 8 кПа.

Подставляем вместо N их значения, записанные через опорную реакцию R_А.

4. Вычисляем N и строим эпюру продольных сил.

5. Определяем нормальные напряжения σ по формуле и строим их эпюры

Строим эпюру нормальных напряжений.

Проверяем прочность.

Задача

Для статически определимого стального ступенчатого бруса построить эпюры продольных сил, нормальных напряжений и перемещений. Проверить прочность бруса. Материал – сталь Ст 3, модуль продольной упругости Е=2·10 5 МПа, допускаемое напряжение [σ]=160МПа.

Строим эпюру N. Все значения откладываем перпендикулярно от нулевой линии в выбранном нами масштабе.

Положительные значения условимся откладывать вправо от нулевой линии, отрицательные — влево.

Строим эпюру σ.

Проверим прочность по условию прочности

Задача на определение перемещений с учетом собственного веса

На стальной стержень действует продольная сила Р и собственный вес (γ = 78 кН/м 3 ). Найти перемещение сечения 1 –1.

Учет собственного веса

Обозначим его как . Оно будет вызываться собственным весом участка с и весом стержня на участке а+в

Определим удлинение от собственного веса стержня выше сечения 1 –1.

Обозначим его как Оно будет вызываться собственным весом участка а+в

Тогда полное перемещение сечения 1-1:

Т.е, сечение 1-1 опустится на 0,022 мм.

Задача

Данная система один раз статически неопределима. Для раскрытия статической неопределимости необходимо решить совместно уравнение равновесия и уравнение совместности деформаций стержней.

Составим деформационную схему — см. рис. Тогда из схемы: (2)

По закону Гука имеем:

Длины стержней: Тогда получим:

Подставим полученное соотношение в уравнение (1):

Определяем напряжение в стержнях:

Допускаемая нагрузка:

В предельном состоянии: Подставим полученные соотношения в уравнение (1):

При сравнении видим увеличение нагрузки:

Задача

Колонна, состоящая из стального стержня и медной трубы, сжимается силой Р. Длина колонны ℓ. Выразить усилия и напряжения, возникающие в стальном стержне и медной трубе.Проведем сечение 1 – 1 и рассмотрим равновесие отсеченной части

Задача статически неопределима. Уравнение совместности деформации запишем из условия, что удлинения стального стержня и медной трубы одинаковы: (2) или Сократим обе части на длину стержня и выразим усилие в медной трубе через усилие в стальном стержне :

(3) Подставим найденное значение в уравнение (1), получим:

При совместной работе всегда сильнее напряжен элемент из материала с большим модулем упругости. При Е_С = 2·10 5 МПа, Е_М = 1·10 5 МПа:

Задача

Составим уравнение статики: ∑y = 0; С + В – Р = 0; (1)

Дополнительное уравнение совместности деформаций: ∆ℓ₁+∆ℓ₂=0,3 мм (2);

Чтобы найти абсолютную деформацию, необходимо знать продольную силу на участке. На первом участке продольная сила равна С, на втором разности (С- Р). Подставим эти значения в выражения абсолютных деформаций: (3)

Тогда напряжения на участках:

Задача на монтажные (начальные) напряжения

На трех стальных стержнях подвешена жесткая балка; стержень 2 выполнен короче проектного. Определить напряжения в стержнях после сборки системы. Дано:

Схема заданной системы

После завершения сборки в данной системе жесткая балка повернется и займет новое положение.

Точки С, D и К переместятся в положения С₁, D₁ и К₁

Согласно картине деформирования СС₁=Δℓ₁, DD₁=Δ−D₁D₂ = Δ−Δℓ₂, KK₁= Δℓ₃, при этом стержни 1 и 3 испытывают сжатие, а стержень 2 – растяжение.

В соответствии со схемой деформирования уравнение равновесия примет вид:

Дополнительные уравнения можно получить на основе анализа схемы деформирования; из подобия треугольников ВСС₁ и BDD₁, треугольников ВСС₁ и BKK₁ следует:

Согласно закона Гука абсолютные деформации:

N₁=14,3 кН (стержень сжат), N₂=71,5 кН (стержень растянут), N₃=42,9 кН (стержень сжат).

Таким образом, искомые напряжения в стержнях имеют значения: Задача решена.

Задача на температурные напряжения

Ступенчатый медный стержень нагревается от температуры t_Н=20ºС до t_К=50ºС. Проверить прочность стержня. Дано:

Уравнение совместности деформаций следует из условия, что перемещения внешних связей равны 0 — W_В=0 или W_К=0. Таким образом:Откуда:

В результате R_B=20723Н.

Нормальные силы и напряжения на участках:

Согласно результатам расчетов σ_max=│69,1│MПа, при этом σ_max Запись опубликована 22.02.2015 автором admin в рубрике Статически неопределимые задачи. Р-С.

Задача

Расчет стержня с зазором. Для стального ступенчатого стержня при наличии зазора между нижним торцом и опорой требуется: построить эпюры нормальных сил и напряжений, перемещений; проверить прочность. Дано: