Сортировка пузырьком как работает

Сортировка пузырьком — это самый простой алгоритм сортировки, который работает путем многократной замены соседних элементов, если они находятся в неправильном порядке.

( 5 1 4 2 8) ( 1 5 4 2 8), здесь алгоритм сравнивает два первых элемента и меняет их местами, так как (5>1).

(1 5 4 2 8) (1 4 5 2 8), меняет элементы местами, так как 4>4>(5>4)

(1 4 5 2 8) (1 4 2 5 8), меняет элементы местами, так как 2>(5>2)

(1 4 2 5 8 ) (1 4 2 5 8 ), ввиду того, что элементы стоят на своих местах (5>8>5), алгоритм не меняет их местами.

( 1 4 2 5 8) ( 1 4 2 5 8)

(1 4 2 5 8) (1 2 4 5 8), меняет элементы местами, так как (4>2)2>

(1 2 4 5 8) (1 2 4 5 8)

Теперь массив полностью отсортирован, но алгоритму это неизвестно. Поэтому ему необходимо осуществить полный проход и определить, что перестановок элементов не было.

Теперь массив отсортирован, и алгоритм может быть завершён.

Ниже в качестве примера приведена сортировка пузырьком С :

Сортировка пузырьком Java

Сортировка пузырьком Python

Приведенная выше сортировка методом пузырька всегда выполняется, даже если массив отсортирован. Ее можно оптимизировать путем остановки алгоритма, применяемой в том случае, если внутренний цикл не произвел никакой замены.

Пузырьковая сортировка Python 3

Метод пузырька C — результат сортировки:

Худшая и средняя сложность времени: O (n * n). Наихудший случай возникает, когда массив отсортирован по обратному адресу.

Сложность наилучшего случая: O (n). Наилучший случай возникает, когда массив уже отсортирован.

Пограничные случаи: сортировка занимает минимальное время (порядок n), когда элементы уже отсортированы.

Сортировка на месте: Да.

В компьютерной графике пузырьковая сортировка популярна благодаря возможности обнаруживать мелкие ошибки ( например, обмен всего двух элементов ) в почти отсортированных массивах и исправлять ее только с линейной сложностью ( 2n ). Например, она используется в алгоритме заполнения полигонов, где ограничивающие линии сортируются по их координате x на определенной линии сканирования ( линия, параллельная оси X ), и с увеличением Y их порядок меняется ( два элемента меняются местами ) только на пересечениях двух линий.

Пожалуйста, оставьте свои комментарии по текущей теме статьи. За комментарии, лайки, дизлайки, отклики, подписки огромное вам спасибо!

Пожалуйста, опубликуйте ваши мнения по текущей теме статьи. За комментарии, лайки, подписки, дизлайки, отклики низкий вам поклон!

Источник

Сортировка пузырьком

В процессе выполнения данного алгоритма элементы с большими значениями оказываются в конце списка, а элементы с меньшими значениями постепенно перемещаются по направлению к началу списка. Образно говоря, тяжелые элементы падают на дно, а легкие медленно всплывают подобно пузырькам воздуха.

В сортировке методом пузырька количество итераций внешнего цикла определяется длинной списка минус единица, так как когда второй элемент становится на свое место, то первый уже однозначно минимальный и находится на своем месте.

Количество итераций внутреннего цикла зависит от номера итерации внешнего цикла, так как конец списка уже отсортирован, и выполнять проход по этим элементам смысла нет.

Пусть имеется список [6, 12, 4, 3, 8].

За первую итерацию внешнего цикла число 12 переместится в конец. Для этого потребуется 4 сравнения во внутреннем цикле:

Результат: [6, 4, 3, 8, 12]

За вторую итерацию внешнего цикла число 8 переместиться на предпоследнее место. Для этого потребуется 3 сравнения:

Результат: [4, 3, 6, 8, 12]

На третьей итерации внешнего цикла исключаются два последних элемента. Количество итераций внутреннего цикла равно двум:

Результат: [3, 4, 6, 8, 12]

На четвертой итерации внешнего цикла осталось сравнить только первые два элемента, поэтому количество итераций внутреннего равно единице:

Результат: [3, 4, 6, 8, 12]

Реализация сортировки пузырьком с помощью циклов for

Пример выполнения кода:

С помощью циклов while

Функция сортировки пузырьком на Python

Источник

Сортировка пузырьком как работает

Сортировка пузырьком (обменная сортировка) – простой в реализации и малоэффективный алгоритм сортировки. Метод изучается одним из первых на курсе теории алгоритмов, в то время как на практике используется очень редко.

Алгоритм состоит из повторяющихся проходов по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются раз или до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При каждом проходе алгоритма по внутреннему циклу, очередной наибольший элемент массива ставится на своё место в конце массива рядом с предыдущим «наибольшим элементом», а наименьший элемент перемещается на одну позицию к началу массива («всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма).

Пример работы алгоритма

Возьмём массив с числами «5 1 4 2 8» и отсортируем значения по возрастанию, используя сортировку пузырьком. Выделены те элементы, которые сравниваются на данном этапе.

(5 1 4 2 8) (1 5 4 2 8), Здесь алгоритм сравнивает два первых элемента и меняет их местами. (1 5 4 2 8) (1 4 5 2 8), Меняет местами, так как 4″ /> (1 4 5 2 8) (1 4 2 5 8), Меняет местами, так как 2″ /> (1 4 2 5 8) (1 4 2 5 8), Теперь, ввиду того, что элементы стоят на своих местах (5″ />), алгоритм не меняет их местами.

(1 4 2 5 8) (1 4 2 5 8) (1 4 2 5 8) (1 2 4 5 8), Меняет местами, так как 2″ /> (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8)

Теперь массив полностью отсортирован, но алгоритм не знает так ли это. Поэтому ему необходимо сделать полный проход и определить, что перестановок элементов не было.

(1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8)

Теперь массив отсортирован и алгоритм может быть завершён.

Реализация алгоритма на различных языках программирования:

Источник

Пузырьковая сортировка (сортировка “пузырьком”)

Алгоритм сортировки массива “пузырьковая сортировка” рассматривается практически во всех учебниках по программированию на С++. Его легко понять начинающим. Он наглядный и очень простой.

На практике этот алгоритм почти никто не использует, так как он медлительный и есть более быстрые и усовершенствованные алгоритмы. Мы также разберем его потому, что сортировка “пузырьком” – это основа некоторых более эффективных алгоритмов, которые будут изложены в следующих статьях. Это “быстрая” сортировка, “пирамидальная” сортировка и “шейкерная” сортировка.

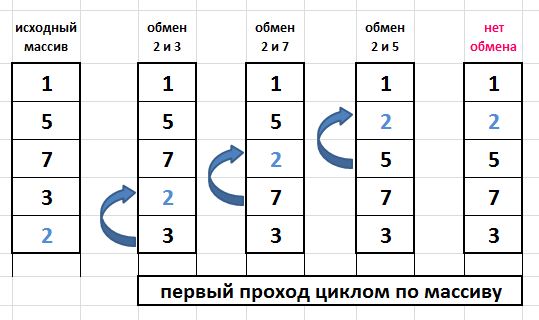
Как работает “пузырьковая” сортировка? Допустим у нас есть неотсортированный массив чисел из 5-ти элементов и нам предстоит разместить значения по возрастанию. Для наглядности, на рисунке изобразим этот массив вертикально “Исходный массив”.

Алгоритм сортировки “пузырьком” состоит в повторении проходов по массиву с помощью вложенных циклов. При каждом проходе по массиву сравниваются между собой пары “соседних” элементов. Если числа какой-то из сравниваемых пар расположены в неправильном порядке – происходит обмен (перезапись) значений ячеек массива.

Образно говоря в нашем примере 2 “легче” чем 3 – поэтому обмен есть, далее 2 “легче” чем 7 – снова обмен и т.д. При сравнении нулевого и первого элемента на нашем рисунке обмена нет, так как 2 “тяжелее” чем 1. Таким образом более “легкое” значение, как пузырек в воде, поднимается вверх до нужной позиции. Вот почему у этого алгоритма такое название.

Рассмотрим алгоритм сортировки “пузырьком” в работе:

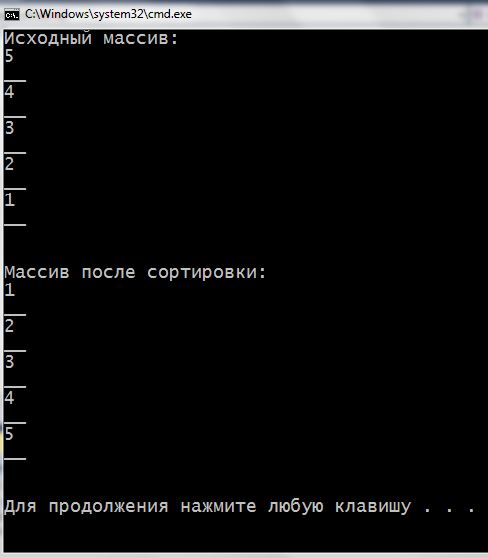
Внимательно разобрав данный пример с подробными комментариями, вам должно быть все понятно. Результат на экране такой:

Дополнить можно следующим: после того, как внутренний цикл отработает один раз, минимальное значение массива будет занимать нулевую ячейку. Поэтому при повторном проходе, очередное минимальное значение из оставшихся надо будет разместить в следующей ячейке (i + 1).

Таким образом нет необходимости сравнивать между собой все элементы массива снова и количество обрабатываемых значений уменьшается на 1. При сортировке “пузырьком” необходимо пройти SIZE – 1 итераций внешнего цикла, так как сравнивать один элемент с самим собой – смысла нет.

Не будем забывать то, о чем мы говорили в самом начале – алгоритм “пузырьковой” сортировки малоэффективен и медлителен. Если у нас есть частично отсортированный массив и необходимо переместить в начало только одно значение, он все равно будет проходить все итерации циклов. То есть производить сравнение уже отсортированных значений массива, хотя этого уже можно и не делать.

Давайте немного улучшим эту ситуацию. Добавим в код еще одну переменную-“флажок”, которая будет давать знать, произошел ли обмен значений на данной внешнего цикла итерации или нет. Перед тем, как войти во внутренний цикл, “флажок” будет сбрасываться в 0.

Если обмен значениями в этом цикле случится – “флажку” будет присвоено значение 1, если нет – то он останется равным 0. В последнем случае (если “флажок” равен 0) – обменов не было и массив полностью отсортирован. Поэтому программе можно досрочно выйти из циклов, чтобы не тратить время попусту на последующие ненужные сравнения.

Источник

Пузырьковая сортировка в C++: главные моменты

Всем привет! Наверно всем прогерам в какой-то момент нужно было отсортировать массив. Сегодня мы разберем алгоритм сортировки с помощью которого вы сможете отсортировать ваш массив или вектор. Вы наверное догадались с названия сегодня пойдет речь о пузырьковой сортировке.

Этот алгоритм очень просто реализовать, но в то же время его главный минус — медленная сортировка.

Что такое пузырьковая сортировка

Пузырьковая сортировка — наверно самая простая сортировка, которую я встречал. Обычно она встречается в книгах по программированию и не выходит за ее пределы. Так как она работает намного медленнее, чем другие алгоритмы сортировки.

Но благодаря ей появились алгоритмы, которые более эффективнее чем она сама. Из таких сортировок можно отметить шейкерную или как еще ее называют сортировка перемешиванием.

Как работает алгоритм пузырьковой сортировки

Принцип работы пузырьковой сортировки можно описать в три пункта:

Ниже вы можете увидеть, как работает пузырьковая сортировка в действии.

Как создать пузырьковую сортировку

Вот что нам придется делать для создания пузырьковой сортировки:

В примере ниже мы предложили пользователю заполнить массив, который мы дальше отсортируем используя пузырьковую сортировку.

Давайте поподробнее разберем строки 16 — 24 (здесь находится пузырьковая сортировка):

Давайте посмотрим, что выведет программа выше при запуске:

Как улучшить пузырьковую сортировку

Ниже вы можете видеть оптимизированную версию пузырьковой сортировки.

Давайте посмотрим, что мы сделали для ее оптимизации:

Дело в том, что за первый полный проход циклом по массиву самый большой элемент всплывет вверх (переместится в конец массива). Второй по размерам элемент всплывет на предпоследнюю ячейку уже за второй проход цикла и т.д.

Вы также можете объявить переменную flag типа int и вместо true или false хранить в переменной значение 1 и 0.

А в строке 9: чтобы мы могли выйти из алгоритма мы проверяем:

Источник