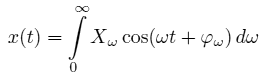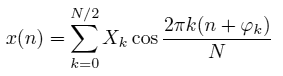Спектрограмма звука как читать
Спектр звука воспринимается как тембр. Спектр звука – это относительная амплитуда всех его частотных составляющих. Звук (с физической точки зрения) – колебания частиц среды. Звук (человеческой речи) – это, как правило, не простое (одиночное), а сложное (комплексное) колебание, характеризующееся наличием более, чем одной частоты. Частота – частота повторений полных колебательных движений в единицу времени. График комплексного колебания – не синусоида, а гораздо более сложная линия. Но сложный тон можно разложить на несколько простых, это и называется спектральным анализом. Спектральный анализ звуков сводится к получению значений частот и амплитуд простых тонов, из которых состоит комплексный звук. Это преобразование основано на теореме Фурье: любое периодическое колебание является суммой гармонический колебаний (простых тонов), частоты которых кратны частоте основного тона, причем эти гармонические колебания различаются по фазе и амплитуде. На спектре: амплитуда – вертикальная ось частота – горизонтальная ось
Спектральная огибающая – линия, соединяющая вершины гармоник спектра. Спектр звука является результатом воздействия одного или нескольких источников на фильтрующую систему речевого аппарата (основное положение акустической теории речеобразования). Гутер Фанн. Связь между акустическим и артикуляторным языковыми характеристиками. Движение языка по вертикали связаны со значением первой форманты, чем выше язык по вертикали, тем более закрыт звук, тем меньше частотное значение первой форманты. По горизонтали – вторая форманта, чем переднее положение языка, тем выше значение второй форманты. 3
фазы любого звука: экскурсия, выдержка, рекурсия.
Все звуки делятся на тоны и шумы. Звуки с периодическими, гармоническими колебаниями – тоны. Звуки, возникающие в результате ряда непериодических колебаний – шумы. В речи тоновые звуки образуются с участием голосовых связок. Шумы – при возникновении каких-либо препятствия в полости рта. Тоновые зв – гл, Шумовые – глух согл. Сонор – тоновые со слабой примесью шума, зв согл – шумовые с участие тона. ТОновыцй звук речи состоит из многих простых колебаний (гармоники). Если отложить на графике по горизонт оси частоты этих гармоник в гц, а по вертик оси – значения интенсивности в децибелах, получится спектр этого звука.
ФОРМАНТА – усиленная частотная обл, которая совпадает с частотами резонанса. Зв речи имеют протяженность во времени, их спектры представляют с помощью трех характеристик: ЧАСТОТА, ИНТЕНСИВНЕОСТЬ, ВРЕМЯ. На таких спектрограммах по горизонт оси – длительность, по вертик оси – частота, об интенсивности свидетельствуют лишь потемнения различных участков спектрограмм. Спектр гл отлич большим уровнем энергии, об этом свидетельствует степень потемнения участков на спектрограмме. На спектрограмме гл отчетливо видны форманты. У согл – уровень энергии гораздо ниже, шумовые спектральные составляющие расположены в высокочастотной обл спектра. Они не образуют формант, а представлены в хаотич беспорядке.
ПО ФОРМЕ СПЕКТРЫ РЕЧИ МОГУТ БЫТЬ:
1. Вокальные (гл и сонор) и невокальные (шум согл). Для характеристики зв по этому признаку важно, есть ли в спектре формантная структура.
2. Консонантные (все согл + сонор) и неконсонантные (гл). Этот признак связан с общем уровнем энергии в спектре. Зв с высоким уровнем энергии неконсонантны.
3. Высокие (гл переднего ряда, передне и средне языч согл)- низкие ()все неперед гл, губные и заднеязыч согл). Для этих зв важно, в какой части спектра преимущ расположены составляющие – в обл низких частот или высоких.
4. Компактные (все остальные) – диффузные(гл верхнего подъема, губ и зуб согл). Компактность зв определяется относительной близостью усиленных составляющих друг к другу и одновременно к центру спектра (1000 гц)Диффузные зв не обладают этим качеством.
5. Диезные (мягк согл, гл перед ряда и гл, которые мы произносим между мягк согл.)- недиезность (тв согл + неперд гл). Признавк диезности связан с более высоким положением в спектре одной или нескольких обл усиления энергии.
6. Бемольные(огубленные гл и согл) – небемольные(остальные). Бемольность – понижение всех или нескольких составляющих зв.
7. Прерванные (смычные согл) – непрерванные (все гл и несмыч согл). У прерванных зв начало отлич большим расходом энергии, который затем не возрастает. У непрерывных расход энергии относительно равномерно распределен во времени.
8. Резкие (аффрикаты и дрожащие) – нерезкие(остальные). Резкие – неоднородность спектра.
9. Звонкие – глухие. Зв – гл и зв согл имеют в спектре низкую интенсивную составляющую(до 300 гц), которая соответствует основному тону зв. Этот тон создается колебаниями голос связок
Алгоритм анализа спектрограмм:
1. Определить сколько звуков
2. Отличить гл от согл. Ударный гл на спектре изображен интенсивнее, гл имеют разную собственную длительность а – 150 мс, е\о – 110 мс, и\у – 80мс (у гл формантная структур, они более интенсивны, частота гл – более 2000 гц, согл – выше 4000 гц, у согл – отсутствие голоса, отсутствие нулевой форманты)
3. Для определения согл основным явл : определение способа и места образования, тв\мг (по соседнему гласному, но не всегда), глух\зв.
Спектрограмма звука как читать
Спектроанализатор – прибор для измерения и отображения спектра сигнала – распределения энергии сигнала по частотам. В этой статье рассматриваются основные виды анализаторов спектра и иллюстрируется их применение для редактирования и реставрации звука. Особое внимание уделяется современным анализаторам, основанным на FFT – быстром преобразовании Фурье.
Зачем анализировать спектр?
Традиционно в цифровой звукозаписи аудиодорожка представляется в виде осциллограммы, отображающей форму звуковой волны (waveform), то есть зависимость амплитуды звука от времени. Такое представление достаточно наглядно для опытного звукорежиссёра: осциллограмма позволяет увидеть основные события в звуке, такие как изменения громкости, паузы между частями произведения и зачастую даже отдельные ноты в сольной записи инструмента. Но одновременное звучание нескольких инструментов на осциллограмме «смешивается» и визуальный анализ сигнала становится затруднительным. Тем не менее, наше ухо без труда различает отдельные инструменты в небольшом ансамбле. Как же это происходит?
Когда сложное звуковое колебание попадает на барабанную перепонку уха, оно с помощью серии слуховых косточек передаётся на орган, называемый улиткой. Улитка представляет собой закрученную в спираль эластичную трубочку. Толщина и жёсткость улитки плавно меняются от края к центру спирали. Когда сложное колебание поступает на край улитки, это вызывает ответные колебания разных частей улитки. При этом резонансная частота у каждой части улитки своя. Таким образом улитка раскладывает сложное звуковое колебание на отдельные частотные составляющие. К каждой части улитки подходят отдельные группы слуховых нервов, передающие информацию о колебаниях улитки в головной мозг (более подробно о слуховом восприятии можно прочитать в статье «Основы психоакустики» И. Алдошиной в журнале «Звукорежиссер» №6, 1999). В результате в мозг поступает информация о звуке, уже разложенная по частотам, и человек легко отличает высокие звуки от низких. Кроме того, как мы вскоре увидим, разложение звука на частоты помогает различить отдельные инструменты в полифонической записи, что значительно расширяет возможности редактирования.
Полосовые спектроанализаторы
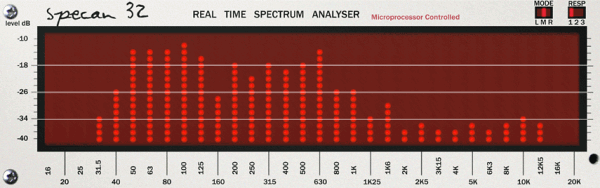
Первые звуковые анализаторы спектра разделяли сигнал на частотные полосы с помощью набора аналоговых фильтров. Дисплей такого анализатора (рис. 1) показывает уровень сигнала во множестве частотных полос, соответствующих фильтрам.
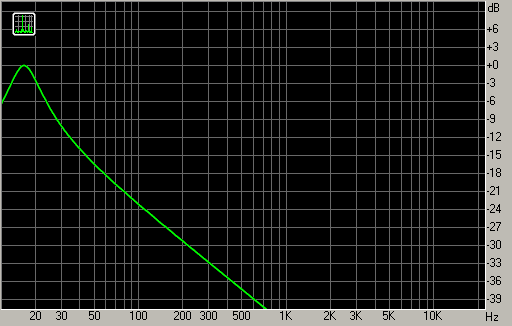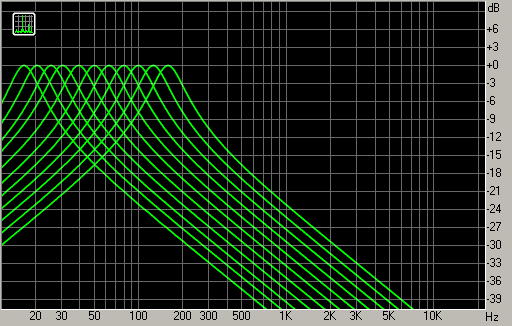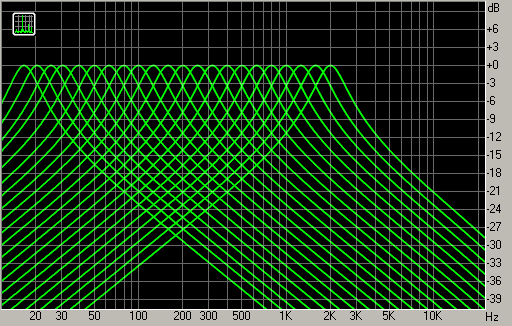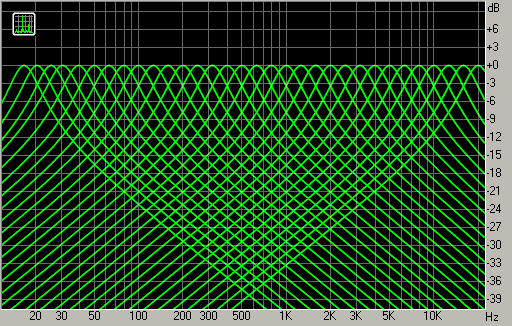
На рис. 2 приведён пример частотных характеристик полосовых фильтров в анализаторе, удовлетворяющем стандарту ГОСТ 17168-82. Такой анализатор называется третьоктавным, так как в каждой октаве частотного диапазона имеется три полосы. Видно, что частотные характеристики полосовых фильтров перекрываются; их крутизна зависит от порядка используемых фильтров.
Важным свойством спектроанализатора является баллистика – инерционность измерителей уровня в частотных полосах. Она может регулироваться заданием скорости нарастания (атаки) и спада уровня. Типичное время атаки и спада в таком анализаторе – порядка 200 и 1500 мс.
Полосовые спектроанализаторы часто применяются для настройки АЧХ (амплитудно-частотной характеристики) акустических систем на концертных площадках. Если на вход такому анализатору подать розовый шум (имеющий одинаковую мощность в каждой октаве), то дисплей покажет горизонтальную линию, с возможной поправкой на вариацию шума во времени. Если розовый шум, проходя через звукоусилительную систему зала, исказился, то изменения его спектра будут видны на анализаторе. При этом анализатор, как и наше ухо, будет малочувствителен к узким провалам АЧХ (менее 1/3 октавы).
Преобразование Фурье
Преобразование Фурье – это математический аппарат для разложения сигналов на синусоидальные колебания. Например, если сигнал x(t) непрерывный и бесконечный по времени, то его можно представить в виде интеграла Фурье:
Интеграл Фурье собирает сигнал x(t) из бесконечного множества синусоидальных составляющих всевозможных частот ω, имеющих амплитуды Xω и фазы φω.
На практике нас больше интересует анализ конечных по времени звуков. Поскольку музыка не является статичным сигналом, её спектр меняется во времени. Поэтому при спектральном анализе нас обычно интересуют отдельные короткие фрагменты сигнала. Для анализа таких фрагментов цифрового аудиосигнала существует дискретное преобразование Фурье:
Здесь N отсчётов дискретного сигнала x(n) на интервале времени от 0 до N–1 синтезируются как сумма конечного числа синусоидальных колебаний с амплитудами Xk и фазами φk. Частоты этих синусоид равны kF/N, где F – частота дискретизации сигнала, а N – число отсчётов исходного сигнала x(n) на анализируемом интервале. Набор коэффициентов Xk называется амплитудным спектром сигнала. Как видно из формулы, частоты синусоид, на которые раскладывается сигнал, равномерно распределены от 0 (постоянная составляющая) до F/2 – максимально возможной частоты в цифровом сигнале. Такое линейное расположение частот отличается от распределения полос третьоктавного анализатора.
FFT-анализаторы
FFT (fast Fourier transform) – алгоритм быстрого вычисления дискретного преобразования Фурье. Благодаря ему стало возможным анализировать спектр звуковых сигналов в реальном времени.
Рассмотрим работу типичного FFT-анализатора. На вход ему поступает цифровой аудиосигнал. Анализатор выбирает из сигнала последовательные интервалы («окна»), на которых будет вычисляться спектр, и считает FFT в каждом окне для получения амплитудного спектра Xk. Вычисленный спектр отображается в виде графика зависимости амплитуды от частоты (рис. 3). Аналогично полосовым анализаторам, обычно используется логарифмический масштаб по осям частот и амплитуд. Но из-за линейного расположения полос FFT по частоте спектр может выглядеть недостаточно детальным на нижних частотах или излишне осциллирующим на верхних частотах.
Если рассматривать FFT как набор фильтров, то, в отличие от полосовых фильтров третьоктавного анализатора, фильтры FFT будут иметь одинаковую ширину в герцах, а не в октавах. Поэтому розовый шум на FFT-анализаторе будет уже не горизонтальной линией, а наклонной, со спадом 3 дБ/окт. Горизонтальной линией на FFT-анализаторе будет белый шум – он содержит равную энергию в равных линейных частотных интервалах.
Параметр N – число анализируемых отсчётов сигнала – имеет решающее значение для вида спектра. Чем больше N, тем плотнее сетка частот, по которым FFT раскладывает сигнал, и тем больше деталей по частоте видно на спектре. Для достижения более высокого частотного разрешения приходится анализировать более длинные участки сигнала. Если сигнал в пределах окна FFT меняет свои свойства, то спектр будет отображать некоторую усреднённую информацию о сигнале со всего интервала окна.
Когда нужно проанализировать быстрые изменения в сигнале, длину окна N выбирают маленькой. В этом случае разрешение анализа по времени увеличивается, а по частоте – уменьшается. Таким образом, разрешение анализа по частоте обратно пропорционально разрешению по времени. Этот факт называется соотношением неопределённостей.
Весовые окна
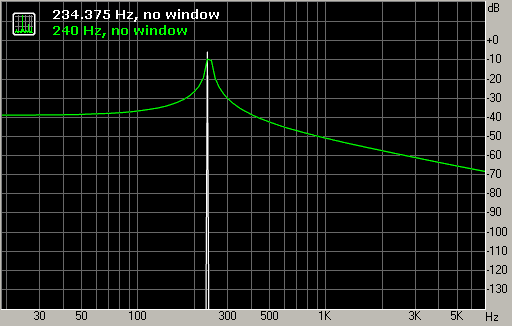
Если частота тона совпадает с одной из частот сетки FFT, то спектр будет выглядеть «идеально»: единственный острый пик укажет на частоту и амплитуду тона (рис. 4, белый график).
Если же частота тона не совпадает ни с одной из частот сетки FFT, то FFT «соберёт» тон из имеющихся в сетке частот, скомбинированных с различными весами. График спектра при этом размывается по частоте (рис. 4, зелёный график). Такое размытие обычно нежелательно, так как оно может закрыть собой более слабые звуки на соседних частотах. Можно также заметить, что амплитуда максимума зелёного графика ниже реальной амплитуды анализируемого тона. Это связано с тем, что мощность анализируемого тона равна сумме мощностей коэффициентов спектра, из которых этот тон составлен.
(наведите мышь для выбора изображения)
Чтобы уменьшить эффект размытия спектра, сигнал перед вычислением FFT умножается на весовые окна – гладкие функции, похожие на гауссиан, спадающие к краям интервала. Они уменьшают размытие спектра за счёт некоторого ухудшения частотного разрешения. Если рассматривать FFT как набор полосовых фильтров, то весовые окна регулируют взаимное проникновение частотных полос.
Простейшее окно – прямоугольное: это константа 1, не меняющая сигнала. Оно эквивалентно отсутствию весового окна. Одно из популярных окон – окно Хэмминга. Оно уменьшает уровень размытия спектра примерно на 40 дБ относительно главного пика.
Весовые окна различаются по двум основным параметрам: степени расширения главного пика и степени подавления размытия спектра («боковых лепестков»). Чем сильнее мы хотим подавить боковые лепестки, тем шире будет основной пик. Прямоугольное окно меньше всего размывает верхушку пика, но имеет самые высокие боковые лепестки. Окно Кайзера обладает параметром, который позволяет выбирать нужную степень подавления боковых лепестков.
Другой популярный выбор – окно Хана. Оно подавляет максимальный боковой лепесток слабее, чем окно Хэмминга, но зато остальные боковые лепестки быстрее спадают при удалении от главного пика. Окно Блэкмана обладает более сильным подавлением боковых лепестков, чем окно Хана.
Для большинства задач не очень важно, какой именно вид весового окна использовать. Главное, чтобы оно было. Популярный выбор – Хан или Блэкман. Использование весового окна уменьшает зависимость формы спектра от конкретной частоты сигнала и от её совпадения с сеткой частот FFT.
Рисунок 4 сделан для синусоид, однако, исходя из него, нетрудно представить, как будет выглядеть спектр реальных звуковых сигналов. Каждый пик в спектре будет иметь некоторую размытую форму, в зависимости от своей частоты и выбранного весового окна.
Чтобы компенсировать расширение пиков при применении весовых окон, можно использовать более длинные окна FFT: например, не 4096, а 8192 отсчета. Это улучшит разрешение анализа по частоте, но ухудшит по времени.
Спектрограмма
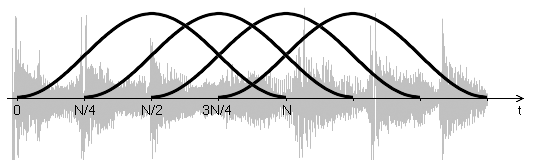
Часто возникает необходимость проследить, как спектр сигнала меняется во времени. FFT-анализаторы помогают сделать это в реальном времени при воспроизведении сигнала. Однако в ряде случаев оказывается удобна визуализация изменения спектра во всём звуковом отрывке сразу. Такое представление сигнала называется спектрограммой. Для её построения применяется оконное преобразование Фурье: спектр вычисляется от последовательных окон сигнала (рис. 5), и каждый из этих спектров образует столбец в спектрограмме.
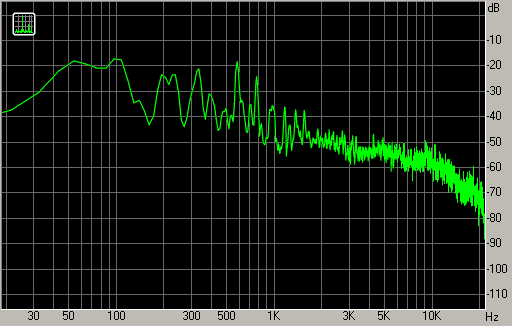
По горизонтальной оси спектрограммы откладывается время, по вертикальной – частота, а амплитуда отображается яркостью или цветом. На спектрограмме гитарной ноты на рис. 6 видно развитие звучания: оно начинается с резкой атаки и продолжается в виде гармоник, кратных по частоте основному тону 440 Гц. Видно, что верхние гармоники имеют меньшую амплитуду и затухают быстрее, чем нижние. Также на спектрограмме прослеживается шум записи – равномерный фон тёмно-синего цвета. Справа показана шкала соответствия цветов и уровней сигнала (в децибелах ниже нуля).
(наведите мышь для выбора изображения)
Если менять размер окна FFT, становится хорошо видно, как меняется частотное и временное разрешение спектрограммы. При увеличении окна гармоники становятся тоньше, и их частота может быть определена более точно. Однако размывается во времени момент атаки (в левой части спектрограммы). При уменьшении размера окна наблюдается обратный эффект.
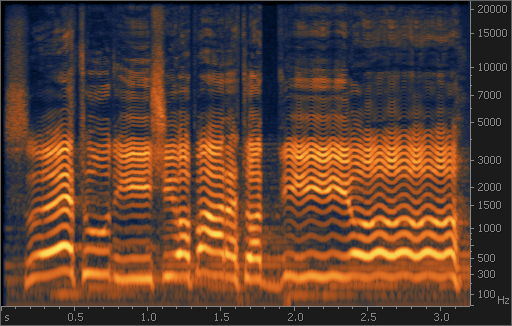
Особенно полезна спектрограмма при анализе быстро меняющихся сигналов. На рис. 7 показана спектрограмма вокального пассажа с вибрато. По ней легко определить такие характеристики голоса, как частота и глубина вибрато, его форма и ровность, наличие певческой форманты. По изменению высоты основного тона и гармоник прослеживается исполняемая мелодия.
(наведите мышь для выбора изображения)
Применения спектрограммы
Современные средства реставрации звука, такие как программа iZotope RX, активно используют спектрограмму для редактирования отдельных частотно-временных областей в сигнале. С помощью этой техники можно найти и подавить такие нежелательные призвуки, как звонок мобильного телефона во время важной записи, скрип стула пианиста, кашель в зрительном зале и т.п.
Проиллюстрируем использование спектрограммы для удаления свиста поклонников из концертной записи.
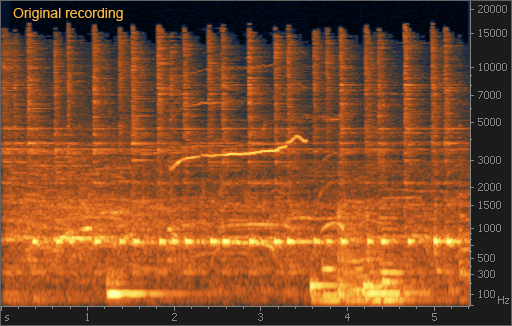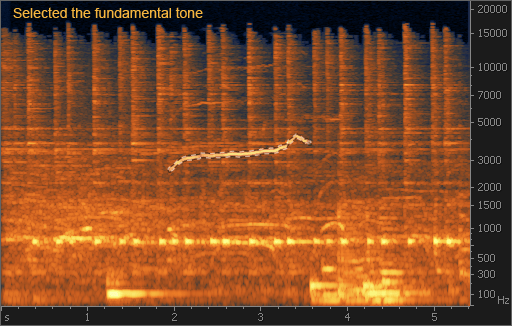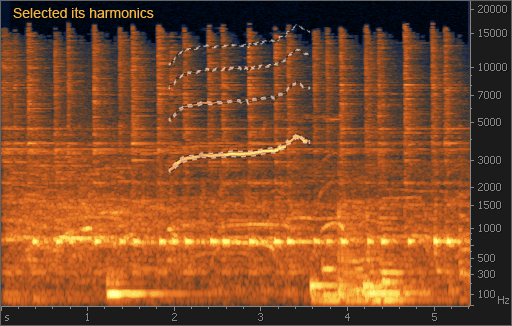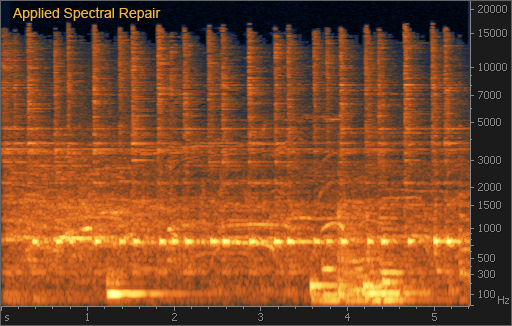
На рис. 8 свист легко находится: это светлая кривая линия в районе 3 кГц. Если бы частота свиста была постоянной, то его можно было бы подавить с помощью режекторного фильтра. Однако в нашем случае частота меняется. Для выделения свиста на спектрограмме удобно воспользоваться инструментом «волшебная палочка» из программы iZotope RX II. Одно нажатие приводит к выделению основного тона свиста, повторное нажатие выделяет гармоники. После этого свист можно удалить, просто нажав на клавишу Del. Однако более аккуратный способ – воспользоваться модулем Spectral Repair: это позволит избежать «дыр» в спектре после удаления свиста. После применения этого модуля в режиме ослабления с вертикальной интерполяцией (Attenuate vertically) свист практически полностью исчезает из записи: как визуально, так и на слух.
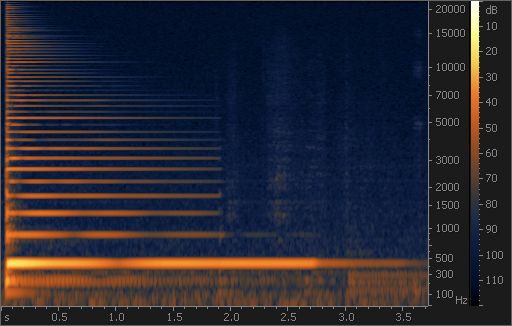
Еще одно полезное применение спектрограммы – анализ присутствия в записи следов компрессии MP3 или других кодеков с потерями. У большинства записей оригинального (несжатого) качества частотный диапазон простирается до 20 кГц и выше; при этом энергия сигнала плавно спадает с ростом частоты (как на рис. 6, 7). В результате психоакустической компрессии верхние частоты сигнала квантуются сильнее нижних, и верхняя граница спектра сигнала обнуляется (как на рис. 8). При этом частота среза зависит от содержания кодируемого сигнала и от битрейта кодера. Ясно, что кодер стремится обнулять только те частоты в сигнале, которые в данный момент не слышны (замаскированы). Поэтому частота среза, как правило, меняется во времени, что образует на спектрограмме характерную «бахрому» с островками энергии на тёмном фоне.
Спектрограмма часто позволяет найти в записи дефекты, которые неочевидны при прослушивании, но могут сказаться при последующей обработке. Например, паразитная наводка от ЭЛТ-видеомонитора на частоте 15–16 кГц может ускользнуть от уха пожилого звукорежиссёра. Однако спектрограмма ясно покажет её в виде горизонтальной линии (рис. 9) и позволит уточнить частоту для настройки режекторного фильтра.
Аналогичная ситуация иногда возникает и с низкочастотными помехами, такими как задувание ветра в микрофон или постоянная составляющая (смещение по постоянному току, DC offset). Они могут располагаться на инфранизких частотах и не обнаруживать себя без помощи спектроанализатора или осциллографа.
Заключение
Среди опытных звукорежиссёров старой школы распространено мнение, что анализировать и редактировать сигналы следует исключительно на слух, не полагаясь на индикаторы и анализаторы. Разумеется, анализаторы – не панацея в случае отсутствия слуха. Вряд ли кто-то серьёзно воспринимает идею сведения композиции «по приборам».
Не отрицая важности критического прослушивания звука на каждой стадии редактирования, мы всё же предлагаем использовать анализаторы спектра в тех задачах, где это может привести к более точным результатам. Конечно, можно определить на слух паразитный тон на частоте 15 кГц и подобрать режекторный фильтр подходящей добротности для его удаления. Но намного проще увидеть этот тон на спектроанализаторе и сразу более точно оценить его свойства: «плывёт» ли частота, есть ли боковые пики. В конечном счёте, это позволит более аккуратно удалить помеху. Аналогичная ситуация и со многими другими задачами редактирования, особенно – в реставрации звука.
Спектр и спектрограмма – способы представления звука, более близкие к слуховому восприятию, нежели осциллограмма. Надеюсь, что эта статья откроет новые возможности в анализе и редактировании звука для тех, кто ранее с этими представлениями не работал.
Распознавание звуков с помощью глубокого обучения
Jan 18 · 5 min read
Вы когда-нибудь просыпались с непонятным ощущением: слышишь какой-то звук, но точно знаешь, что в этом звуке что-то не то?
Распознавание звуков — это один базовых инстинктов, позволявших людям избегать опасности. Это умение помогало нам узнавать о приближении хищника. Да и сейчас звуки продолжают играть большую роль в нашей жизни: мы различаем человеческие голоса, наслаждаемся музыкой и пением птиц.
Поэтому совершенно естественно, что важней ш ей задачей стала разработка аудиоклассификаторов. Они необходимы для того, чтобы классифицировать источник звука, и уже широко применяются в различных целях. Так, в музыке существует классификатор музыкальных жанров. В последнее время подобные системы стали использоваться и для классификации звуков, издаваемых птицами. Раньше этим занимались орнитологи. Цель этих систем — распределить птиц по категориям. Задача непростая с учётом того, как сложно уловить звуки, издаваемые птицами в полях или шумных окрестностях.
В последнее время глубокое обучение превратилось в одну из самых популярных технологий для решения множества задач. Произошло это благодаря точности глубокого обучения, а также совершенствованию вычислительных устройств, таких как CPU (центральный процессор) и GPU (графический процессор). На приведённой ниже диаграмме показано, насколько важен рынок глубокого обучения, а также его ожидаемый размер с точки зрения программного обеспечения, аппаратного оборудования и услуг:
В этой статье наша задача — считывание аудиофайла со звуками, издаваемыми птицами (количество: от нуля до нескольких звуков). Кроме того, мы задействуем глубокое обучение для выявления, какой птице какой звук принадлежит. Будем использовать для этого Cornell Birdcall Identification Challenge, в котором мы получили серебряную медаль (с высоким результатом 2%).
Как обращаться с данными
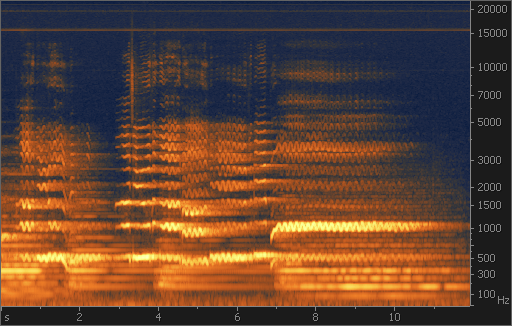
Обработке аудиоданных с получением спектрограммы посвящено бесчисленное множество статей с объяснениями, как загружать звуковые данные, в том числе переводить их в формат спектрограммы, и почему это важно. Вот спектрограмма звуков, издаваемых птицами, на примере мухоловки ольховой и фотография этой птицы (на случай если вам интересно):
Создаём процессор для спектрограммы
torchlibrosa — это библиотека Python, в которой есть несколько функций обработки аудиосигналов, реализованных в PyTorch с возможностью использовать ресурсы графического процессора. PyTorch позволяет запускать алгоритм этой спектрограммы на графическом процессоре. Вот пример извлечения функций спектрограммы с помощью torchlibrosa :
Загружаем аудиоданные
Аудиоданные загрузим через одну из популярных на Python библиотек обработки аудиосигналов librosa :
Обрабатываем спектрограмму
Скорость обработки при тестировании
Мы просто взяли аудио из данных, полученных в ходе проведения Cornell Birdcall Identification Kaggle Challenge (всё из открытого доступа), и сравнили, сколько времени она занимает на центральном процессоре и графическом процессоре. Тестировали на Colab с целью воспроизвести производительность. Оказалось, что обработка log-mel спектрограммы из 5 минутного аудио происходит примерно в 15 раз быстрее на графическом процессоре, чем на центральном процессоре.
Как классифицировать звук
Таким образом, глубокое обучение показало блестящие результаты в аудиосфере. Оно правильно улавливает многочисленные паттерны целевых классов в данных временных рядов. Более важным представляется окружение, в котором птицы издают звуки, и соответствующие данные. Окружающая обстановка (полевые или горные условия) является источником разнообразных шумов, смешивающихся со звуками, издаваемыми птицами. На продолжительной записи могут быть запечатлены звуки нескольких птиц. Поэтому нужно создать аудиоклассификатор со множеством меток и надёжным распознаванием звуков.
Представим архитектуру глубокого обучения, использованную на конкурсе Cornell Birdcall Identification Kaggle Challenge.
Архитектура
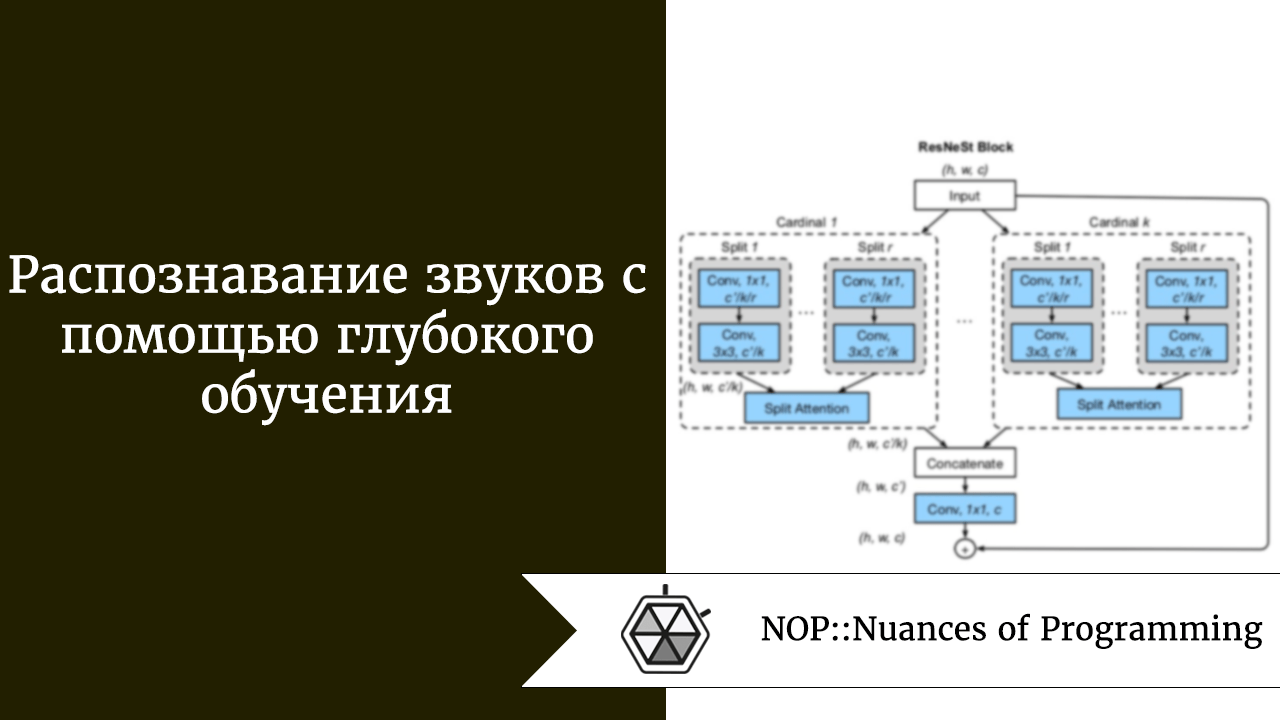
Это принципиально новая архитектура аудиоклассификатора, которая эффективно улавливает характеристики временных рядов за счёт использования CNN (свёрточной нейронной сети), RNN (рекуррентной нейронной сети) и механизмов внимания. Вот небольшая блочная диаграмма архитектуры, которая была представлена на этом конкурсе:
В качестве входных данных архитектуры используем ещё не обработанное аудио с log-mel спектрограммой. Оно проходит через магистральную сеть ResNeSt50, которая является одной из архитектур классификации изображений. После этого доставляем функции, содержащие пространственную и временную информацию, к слоям RoI pooling (области интереса) и bi-GRU (двунаправленным рекуррентным блокам). В этих слоях улавливается информация, касающаяся времени, и уменьшается размер функции. Ведь мы посчитали, что извлечение временных функций имеет решающее значение для классификации количества звуков, издаваемых птицами, в продолжительном аудио. И в заключение передаём данные в механизм внимания, чтобы оценить результаты по каждому временному шагу и выявить, на каком временном шаге проявляют себя птицы.
Обучаем модель
Важно не только создать архитектуру глубокого обучения для представления данных, но и научиться обучать модель (так называемый «рецепт обучения»). Чтобы классифицировать аудио с шумным фоном, в которых есть различные звуки, издаваемые птицами, смешиваем все эти звуки в аудио с шумами, такими как «белый шум». А что касается многочисленных вариаций звуков, издаваемых птицами, увеличиваем высоту звука и маскируем некоторые аудиокадры с помощью SpecAugment.
Вот краткий пример (смешанная версия мухоловки ольховой и американской шилоклювки) тех аугментаций, которые мы применяли.
Заключение
Вы когда-нибудь просыпались с непонятным ощущением: слышишь какой-то звук, но точно знаешь, что в этом звуке что-то не то? С помощью алгоритмов машины смогут избавить вас от непонятных звуков, чтобы вам спалось лучше.