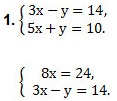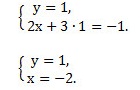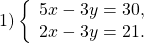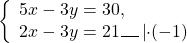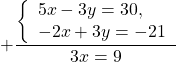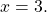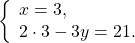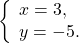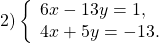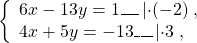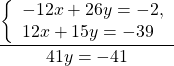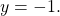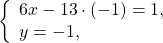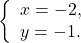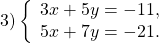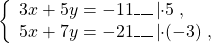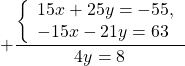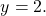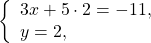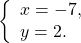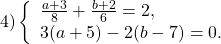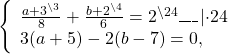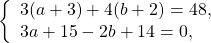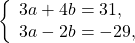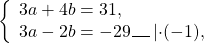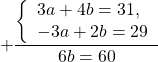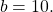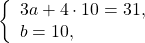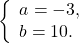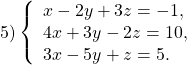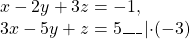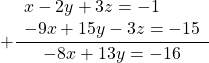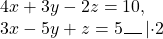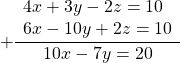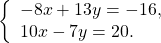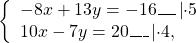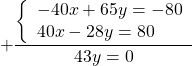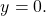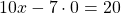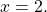Способ сложения как решать
6.9.3. Решение систем линейных уравнений методом сложения.
Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:
1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;
2) сложить почленно полученные уравнения и найти значение одной из переменных;
3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.
Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).
Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.
Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24. Вторым уравнением системы можно записать любое уравнение исходной системы.
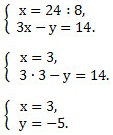
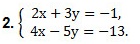
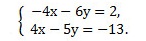
Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):
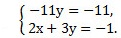
Ответ: (-2; 1).
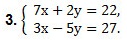
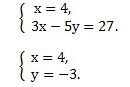
Системы уравнений
Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.
Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют « x » и « y »), которые объединены в общую систему фигурной скобкой.
Например, система уравнений может быть задана следующим образом.
| x + 5y = 7 |
| 3x − 2y = 4 |
Чтобы решить систему уравнений, нужно найти и « x », и « y ».
Как решить систему уравнений
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки
или
«железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
| x + 5y = 7 |
| 3x − 2y = 4 |
Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».
Чтобы выразить неизвестное, нужно выполнить два условия:
Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.
При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.
| x = 7 − 5y |
| 3x − 2y = 4 |
Теперь, вместо « x » подставим во второе уравнение полученное выражение
« x = 7 − 5y » из первого уравнения.
| x = 7 − 5y |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.
| x = 7 − 5y |
| 3(7 − 5y) − 2y = 4 (*) |
Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.
| x = 7 − 5y |
| y = 1 |
| x = 7 − 5 · 1 |
| y = 1 |
| x = 2 |
| y = 1 |
Ответ: x = 2; y = 1
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.
| x + 5y = 7 |
| 3x − 2y = 4 |
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 |
| + => | x + 5y + 3x − 2y = 11 |
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
| x + 5y = 7 |
| 3x − 2y = 4 |
Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».
Для этого умножим первое уравнение на « −3 ».
При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) |
| 3x − 2y = 4 |
| x · (−3) + 5y · (−3) = 7 · (−3) |
| 3x − 2y = 4 |
| −3x −15y = −21 |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 |
| + => | − 3x − 15y + 3x − 2y = −21 + 4 |
| 3x − 2y = 4 | −17y = −17 |:(−17) |
| y = 1 |
Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».
| x = 7 − 5y |
| y = 1 |
| x = 7 − 5 · 1 |
| y = 1 |
| x = 2 |
| y = 1 |
Ответ: x = 2; y = 1
Пример решения системы уравнения
способом подстановки
Выразим из первого уравнения « x ».
| x = 17 + 3y |
| x − 2y = −13 |
Подставим вместо « x » во второе уравнение полученное выражение.
| x = 17 + 3y |
| (17 + 3y) − 2y = −13 (*) |
Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».
| x = 17 + 3y |
| y = −30 |
| x = 17 + 3 · (−30) |
| y = −30 |
| x = 17 −90 |
| y = −30 |
| x = −73 |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения
способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 |
| 2x −2y + 3y = 4 |
| 2x − 3y = −4 |
| 2x + y = 4 |
Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».
Для этого достаточно умножить первое уравнение на « −1 ».
| 2x − 3y = −4 | ·(−1) |
| 2x + y = 4 |
| 2x · (−1) − 3y · (−1) = −4 · (−1) |
| 2x + y = 4 |
| −2x + 3y = 4 |
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только « y » в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 |
| + => | − 2x + 3y + 2x + y = 4 + 4 |
| 2x + y = 4 | 4y = 8 | :4 |
| y = 2 |
Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».
Решение системы уравнений методом сложения
Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.
Способ сложения состоит из трёх простых шагов:
Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.
Однако на практике всё не так просто. Причин тому несколько:
Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:
Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.
Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.
Вообще, существует два метода решения подобных систем:
Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.
Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.
Решение легких задач с применением способа сложения
Итак, учимся применять метод сложения на примере двух простейших выражений.
Задача № 1
Решаем простейшую конструкцию:
Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:
Задача № 2
Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:
Мы получили простейшее линейное уравнение, давайте решим его:
Важные моменты
Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:
В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.
Решение легких задач с применением метода вычитания
Задача № 1
Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:
\[16x=32\left| :16 \right.\]
Задача № 2
Нюансы решения
Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.
Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.
Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.
Решение задач методом домножения на коэффициент
Пример № 1
Пример № 2
\[\left\< \begin
Нюансы решения
Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:
Решение задач с дробными числами
Пример № 1
Вычитаем уравнения друг из друга:
Пример № 2
\[\left\< \begin
Применяем метод вычитания:
Нюансы решения
Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.
Решение сложных систем уравнений
В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.
Система № 1
\[\left\< \begin
Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.
\[3\left( 2x-y \right)+5=-2\left( x+3y \right)+4\]
\[6\left( y+1 \right)-1=5\left( 2x-1 \right)+8\]
Итого мы получим окончательную систему, которая равносильна исходной:
Система № 2
Преобразуем первое выражение:
\[4\left( a-3b \right)-2a=3\left( b+4 \right)-11\]
Разбираемся со вторым:
\[-3\left( b-2a \right)-12=2\left( a-5 \right)+b\]
Итого, наша первоначальная система примет такой вид:
Вычитаем из первой конструкции вторую:
Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.
С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.
При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2
В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.
Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Решить систему уравнений
Немного теории.
Решение систем линейных уравнений. Способ подстановки
Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Пара (1;4) — решение системы
Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.
Решение систем линейных уравнений способом сложения
Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.
Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.
Примеры решения систем линейных уравнений способом сложения
Рассмотрим конкретные примеры решения систем линейных уравнений способом сложения.
Ищем наибольший общий делитель коэффициентов при каждой из переменных (коэффициенты берем со знаком «+»).
Наименьшее общее кратное коэффициентов при x — НОК(5;2)=10, при y — НОК(3;3)=3.
Теперь подставим x=3 в любое из уравнений системы, например, во второе:
Решаем это уравнение:
Ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
НОК(6; 4)=12, НОК(13; 5)=65. Проще работать с коэффициентами перед x.
и сложим почленно левые и правые части уравнений:
НОК(3; 5)=15, НОК(5; 7)=35. Проще получить противоположные числа перед x.
и сложим почленное левые и правые части полученных уравнений:
Подставляем y=2 в первое уравнение системы и находим x:
Прежде чем применить способ сложения, данную систему следует упростить. Умножим первое уравнение на наименьший общий знаменатель дробей, во втором раскроем скобки:
Подставляем найденное значение b в первое уравнение системы (линейных уравнений):
Систему линейных уравнений с тремя переменными можно решить, сначала исключив одно из неизвестных, а затем — другое.
В данной системе проще всего исключить переменную z.
Ко второму уравнению прибавим третье, умноженное на 2:
Получили систему линейных уравнений с двумя переменными:
НОК(8;10)=40, НОК(13; 7)=91. Проще работать с x:
Подставив полученные значение y во второе уравнение системы с двумя переменными, найдём x:
Подставив значения y и x в третье уравнение системы с тремя переменными, найдём z: