Степень дроби как считать
Дробная степень
Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
При a
Выполнить возведение в дробную степень:
Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
Смешанное число нужно предварительно перевести в неправильную дробь:
А как вычисляется отрицательная дробная степень?
Степень с отрицательным рациональным показателем также определена только для a>0:
При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу:
Выполнить возведение в степень с отрицательным рациональным показателем:
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: d i = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 11 2 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6) 2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6) 2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,5 2 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14) 3 = (0,78) 3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32) 3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Ответ на 0 0 может быть любым. Поэтому для избежания путаницы считают, что решение записи 0 0 не имеет смысла, так же как и деление на ноль. Например, (12 / 34) 0 = 12 0 / 34 0 = 1 / 1 = 1 или (-3 / 4) 0 = 1, а вот для (0 / 23) 0 ответ будет не определён.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
Возведение в степень: правила, примеры
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Решение
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Решение
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи 
От основания степени это не зависит.
Как возвести число в целую степень
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Решение
Решение
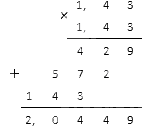
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
Как возвести число в дробную степень
Проиллюстрируем на примере.
Решение
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Решение
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Вычислите приближенное значение 2 в степени 1,174367.
Решение
Дробная степень числа
Дробный показатель
Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:
Поэтому извлечение корня всегда может быть заменено возведением в степень.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При доказательстве этого положения, будем сначала предполагать, что члены дробей: 

В частном случае n или q могут равняться единице.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.
Возведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
В алгебре, пожалуй, одной из самых распространённых операций является возведение дроби в степень. Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: d i = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 11 2 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6) 2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6) 2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,5 2 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14) 3 = (0,78) 3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32) 3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Ответ на 0 0 может быть любым. Поэтому для избежания путаницы считают, что решение записи 0 0 не имеет смысла, так же как и деление на ноль. Например, (12 / 34) 0 = 12 0 / 34 0 = 1 / 1 = 1 или (-3 / 4) 0 = 1, а вот для (0 / 23) 0 ответ будет не определён.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.