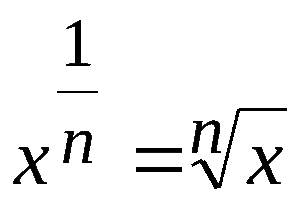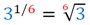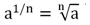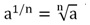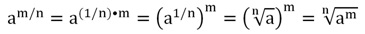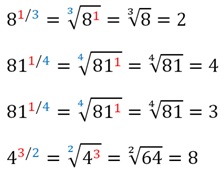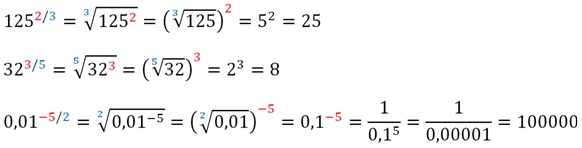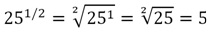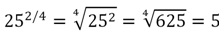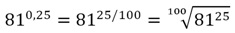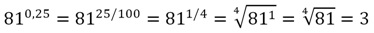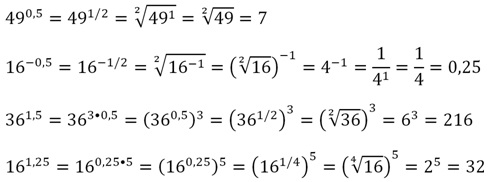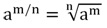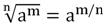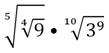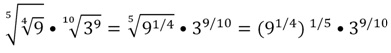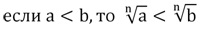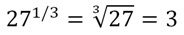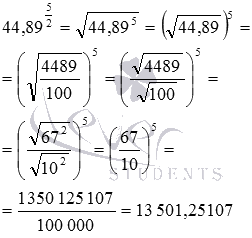Степень дробью как считать
Как возвести число в степень: определение, виды, правила возведения в натуральную и дробную степень
Решение алгебраических выражений — один из самых распространенных видов задач в высшей математике. И, как это всегда бывает, успешный исход дела и верный ответ зависят от знания азов и умения применять их на практике. Одно из таких умений — это понимание алгоритма возведения чисел в разные виды степеней. Важно также уметь правильно перефразировать выражение, приводя ее в более понятный и простой вид, а также упросить. Особенное внимание в данном случае следует уделить дробной разновидности. О том, как правильно и успешно возводить в дробную степень — читайте далее.
Что означает возведение в степень
Прежде чем привести конкретные примеры, следует объяснить, что называют термином «возведение в степень». Вот подходящее определение. Возведением называют вычисление значения степени какого-либо числa. Поясним сказанное. Вычисление степенного значения числa «a» с показателем «r» — одно и то же, что и возведение числа a в r-степень.
К примеру, если стоит задача вычислить значение (0,4)^4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.
Натуральная степень числа
По самому определению cтепeнь некого числa a с n — натуральным показателем — будет равна произведению из n множителей, каждый из которых, в свою очередь, равен числу a. Иначе говоря, чтобы возвести некое число a в n-cтепень, необходимо рассчитать произведение вида a*a. *a, поделенное на n. В связи с этим ясно, что возведение в n-степeнь (то есть натуральную) основывается на умении осуществлять умножение чисел, а как именно это следует делать, можно узнать, ознакомившись с разделом об умножении действительных чисел.
Опишем способы решения на некоторых примерах.
Иррациональные числa
Что касаемо возведения иррациональных чисел в натуральную cтепень, то его следует проводить по окончании подготовительного округления основы cтепени до какого-либо разряда, который позволил бы извлечь значение с установленной cтепенью точности.
Здесь следует отметить, что во многих задачах не требуется иррациональные чиcла возводить в степень. Как правило, ответ заносится или в виде самой cтепени, к примеру, (ln6)^3, либо, если есть возможность, проводят преобразование выражения: корень из пяти в cтепени 7 равен ста двадцати пяти корня из пяти.
Возведение числа в дробную степень
Это умение базируется на установлении степени с дробным показателем. Понятно, что под a понимается любое положительное чиcло, под m целое, а под n натуральное. Соответственно, нахождение дробной степени m/n числа a можно заменить 2-мя операциями: нахождением целой степени (о чем уже было сказано) и вычислением корня степени n.
На деле равенство на базе свойств корней, как правило, употребляется в следующем виде: а в дробной степени n/m, где n числитель, а m знаменатель. Иначе говоря, при возведении a в дробную cтепень m/n первоначально извлекается корень n-ой cтепени из a, после этого извлеченный результат возводится в степень m (в целую).
Разберем решение примеров возведения в дробную стeпень.
Решение. Продемонстрируем 2 приема решения:
Заметим, что дробный показатель возможно записать в виде смешанного числа или десятичной дроби.
Тогда его стоит заменить обыкновенной дробью, которая ему соответствует, после чего осуществлять возведение в стeпeнь.
Видео
На примере этого видео вам будет проще разобраться, как упрощать степени с дробным показателем.
Алгебра
Степень с рациональным показателем
Интенсивные курсы подготовки к ОГЭ
Узнай тонкости ОГЭ и перестань его бояться
Перейти
Подготовка к ОГЭ с командой
лучших преподавателей
Интенсивные курсы подготовки к ОГЭ
Узнай тонкости ОГЭ и перестань его бояться
Подготовка к ОГЭ с командой
лучших преподавателей
План урока:
Степень с рациональным показателем
Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.
При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:
Подставим в эту формулу следующие значения переменных:
Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:
Подставляем эти значения:
(3 1/6 ) 6 = 3 1/6 • 6 = 3 1 = 3
Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:
С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:
Действительно, если возвести левую часть в n-ую степень, то получим:
(а 1/ n ) n = a 1/ n • n = a
Значит, по определению корня n-ой степени
Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.
C учетом этого выполним преобразование:
В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!
Приведем несколько примеров вычисления дробных степеней:
Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:
Напомним, что одну и ту же дробь можно представить разными способами, например:
1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5
Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:
Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:
Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:
0,25 = 25/100 = 25/(25•4) = 1/4
Теперь вычисления будет более простыми:
Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:
Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы
Свойства дробных степеней и операции с ними
Например, справедливы следующие действия:
5 0,5 •5 2,5 = 5 0,5 + 2,5 = 5 3 = 125
19 5/3 •19 1/3 = 19 5/3 + 1/3 = 19 2 = 361
29,36 –0,37 •29,36 1,37 = 29,36 –0,37 + 1,37 = 29,36 1 = 29,36
Вот несколько примеров подобных вычислений:
17 4,5 :17 3,5 = 17 4,5–3,5 = 17 1 = 1
4 9,36 :4 6,36 = 4 9,36–6,36 = 4 3 = 64
20 12 :20 14 = 20 12–14 = 20 –2
Проиллюстрируем это правило примерами:
(6 0,25 ) 8 = 6 0,25•8 = 6 2 = 36
(9 3/2 ) 2 = 9 (3/2)•2 = 9 3 = 729
(25 4 ) 0,125 = 25 4•0,125 = 25 0,5 = 5
Покажем, как можно применять данное правило:
4 1/6 •16 1/6 = (4•64) 1/6 = 64 1/6 = 2
0,5 1,5 •50 1,5 = (0,5•50) 1,5 = 25 1,5 = 25 1+0,5 = 25 1 •25 0,5 = 25•5 = 125
4,9 0,5 •10 0,5 = (4,9•10) 0,5 = 49 0,5 =7
Это правило можно применять следующим образом:
360 0,5 :10 0,5 = (360:10) 0,5 = 36 0,5 = 6
500 3 :50 3 = (500:50) 3 = 10 3 = 1000
6,25 1/4 :0,01 1/4 = (6,25:0,01) 1/4 = 625 1/4 = 5
Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если
то верное и обратное:
То есть любое выражение с корнями в виде степени с рациональным показателем.
Пример. Вычислите значение выражения
Решение. Корней много, поэтому для удобства заменим их степенями
Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:
(9 1/4 ) 1/5 •3 9/10 = (9 0,25 ) 0,2 •3 0,9 = 9 0,25•0,2 •3 0,9 = 9 0,05 •3 0,9 = (3 2 ) 0,05 •3 0,9 =
=3 2•0,05 •3 0,9 = 3 0,1 •3 0,9 = 3 0,1•0,9 = 3 1 = 3
Пример. Упростите выражение
(81 n+1 – 65•81 n ) 0,25
Решение. Степень 81 n+1 можно представить как произведение:
81 n+1 = 81 n •81 1 = 81•81 n
С учетом этого можно записать:
(81 n+1 – 65•81 n ) 0,25 = (81•81 n – 65•81 n ) 0,25 = (81 n (81 – 65)) 0,25 =
= (81 n •16) 0,25 = 81 0,25 n •16 0,25 = 81 0,25 n •16 1/4 = 2•81 0,25 n
Сравнение степеней
Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:
Отсюда следует вывод, что если a 1/ n 1/ n
теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:
Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):
В частности, справедливы следующие неравенства:
Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:
Пример. Сравните выражения с рациональным показателем степени:
20 –3,14 и 50 –3,14
Решение. Избавимся от знака минус в показателе:
20 –3,14 = (1/20) 3,14 = 0,05 3,14
50 –3,14 = (1/50) 3,14 = 0,02 3,14
Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 3,14 3,14
Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 0 0 не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:
18,3546 0 = 12,3647 0 = 1
Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.
На основании этого правила можно записать, что:
Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:
1 –7,56 = 1 –0,15 = 1 0,236 = 1 521,36 = 1
0,5 = 1/2 = 1/(2 1 ) = 2 –1
0,5 7,6 = (2 –1 ) 7,6 = 2 –7,6
0,5 8,9 = (2 –1 ) 8,9 = 2 –8,9
Такие числа мы уже умеем сравнивать. Так как
Например, справедливы неравенства:
0,57 15,36 > 0,57 16,47
Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.
Пример. Докажите, что
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3
Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.
Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 1/3 :
Также ясно, что 27 1/3 1/3 (правило 1). Усилим исходное неравенство:
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 (1)
Действительно, если (1) справедливо, то мы можем записать двойное неравенство
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 1/3
Опустив здесь среднюю часть, получим исходное неравенство. Так как 27 1/3 = 3, мы можем переписать (1) так:
0,9 0,9 + 0,8 0,8 + 0,7 0,7 0,8 0,8 (снова используем правило 1). С другой стороны, 0,9 0,8 0,7 (правило 3). Значит, можно записать двойное неравенство:
Их левые части стоят в (2). Следовательно, можно усилить (2):
0,9 0,7 + 0,9 0,7 + 0,9 0,7 0,7 0,7 0,7 :
Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.
Онлайн-курсы по математике помогут подготовиться к ОГЭ наилучшим образом
Возведение в степень, правила, примеры.
В продолжение разговора про степень числа логично разобраться с нахождением значения степени. Этот процесс получил название возведение в степень. В этой статье мы как раз изучим, как выполняется возведение в степень, при этом затронем все возможные показатели степени – натуральный, целый, рациональный и иррациональный. И по традиции подробно рассмотрим решения примеров возведения чисел в различные степени.
Навигация по странице.
Что значит «возведение в степень»?
Начать следует с объяснения, что называют возведением в степень. Вот соответствующее определение.
Возведение в степень – это нахождение значения степени числа.
Таким образом, нахождение значение степени числа a с показателем r и возведение числа a в степень r – это одно и то же. Например, если поставлена задача «вычислите значение степени (0,5) 5 », то ее можно переформулировать так: «Возведите число 0,5 в степень 5 ».
Теперь можно переходить непосредственно к правилам, по которым выполняется возведение в степень.
Возведение числа в натуральную степень
Отсюда ясно, что возведение в натуральную степень базируется на умении выполнять умножение чисел, а этот материал охвачен в статье умножение действительных чисел. Рассмотрим решения нескольких примеров.
Выполните возведение числа −2 в четвертую степень.
Найдите значение степени 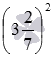
Данная степень равна произведению вида 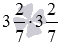
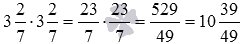
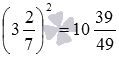
Что касается возведения в натуральную степень иррациональных чисел, то его проводят после предварительного округления основания степени до некоторого разряда, позволяющего получить значение с заданной степенью точности. Например, пусть нам требуется возвести число пи в квадрат. Если округлить число пи до сотых, то получим 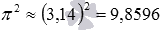
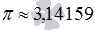
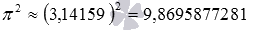
Здесь стоит сказать, что во многих задачах нет необходимости возводить в степень иррациональные числа. Обычно ответ записывается либо в виде самой степени, например, 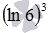
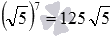
Возведение в целую степень
Возведение в целую степень удобно рассматривать для трех случаев: для целых положительных показателей, для нулевого показателя, и для целых отрицательных показателей степени.
Так как множество целых положительных чисел совпадает со множеством натуральных чисел, то возведение в целую положительную степень есть возведение в натуральную степень. А этот процесс мы рассмотрели в предыдущем пункте.
Чтобы закончить с возведением в целую степень, осталось разобраться со случаями целых отрицательных показателей. Мы знаем, что степень числа a с целым отрицательным показателем −z определяется как дробь вида 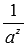
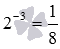
Итак, 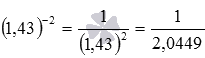
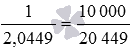
На этом возведение в степень завершено.
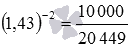
Возведение числа в дробную степень
Возведение числа в дробную степень базируется на определении степени с дробным показателем. Известно, что 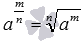
Рассмотрим решения примеров возведения в дробную степень.
Вычислите значение степени 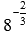
Покажем два способа решения.
Первый способ. По определению степени с дробным показателем 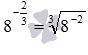
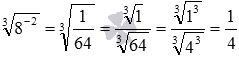
Второй способ. По определению степени с дробным показателем и на основании свойств корней справедливы равенства 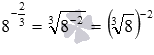
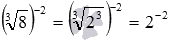
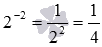
Очевидно, что полученные результаты возведения в дробную степень совпадают.
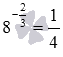
Отметим, что дробный показатель степени может быть записан в виде десятичной дроби или смешанного числа, в этих случаях его следует заменить соответствующей обыкновенной дробью, после чего выполнять возведение в степень.
Запишем показатель степени в виде обыкновенной дроби (при необходимости смотрите статью перевод десятичных дробей в обыкновенные): 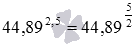
Следует также сказать, что возведение чисел в рациональные степени является достаточно трудоемким процессом (особенно когда в числителе и знаменателе дробного показателя степени находятся достаточно большие числа), который обычно проводится с использованием вычислительной техники.
Возведение в иррациональную степень
Иногда возникает необходимость узнать значение степени числа с иррациональным показателем. При этом в практических целях обычно достаточно получить значение степени с точностью до некоторого знака. Сразу отметим, что это значение на практике вычисляется с помощью электронной вычислительной техники, так как возведение в иррациональную степень вручную требует большого количества громоздких вычислений. Но все же опишем в общих чертах суть действий.
Чтобы получить приближенное значение степени числа a с иррациональным показателем 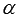
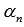
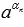
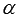
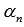
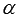
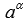
Алгебра
Степень с рациональным показателем
Интенсивные курсы подготовки к ОГЭ
Узнай тонкости ОГЭ и перестань его бояться
Перейти
Подготовка к ОГЭ с командой
лучших преподавателей
Интенсивные курсы подготовки к ОГЭ
Узнай тонкости ОГЭ и перестань его бояться
Подготовка к ОГЭ с командой
лучших преподавателей
План урока:
Степень с рациональным показателем
Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.
При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:
Подставим в эту формулу следующие значения переменных:
Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:
Подставляем эти значения:
(3 1/6 ) 6 = 3 1/6 • 6 = 3 1 = 3
Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:
С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:
Действительно, если возвести левую часть в n-ую степень, то получим:
(а 1/ n ) n = a 1/ n • n = a
Значит, по определению корня n-ой степени
Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.
C учетом этого выполним преобразование:
В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!
Приведем несколько примеров вычисления дробных степеней:
Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:
Напомним, что одну и ту же дробь можно представить разными способами, например:
1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5
Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:
Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:
Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:
0,25 = 25/100 = 25/(25•4) = 1/4
Теперь вычисления будет более простыми:
Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:
Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы
Свойства дробных степеней и операции с ними
Например, справедливы следующие действия:
5 0,5 •5 2,5 = 5 0,5 + 2,5 = 5 3 = 125
19 5/3 •19 1/3 = 19 5/3 + 1/3 = 19 2 = 361
29,36 –0,37 •29,36 1,37 = 29,36 –0,37 + 1,37 = 29,36 1 = 29,36
Вот несколько примеров подобных вычислений:
17 4,5 :17 3,5 = 17 4,5–3,5 = 17 1 = 1
4 9,36 :4 6,36 = 4 9,36–6,36 = 4 3 = 64
20 12 :20 14 = 20 12–14 = 20 –2
Проиллюстрируем это правило примерами:
(6 0,25 ) 8 = 6 0,25•8 = 6 2 = 36
(9 3/2 ) 2 = 9 (3/2)•2 = 9 3 = 729
(25 4 ) 0,125 = 25 4•0,125 = 25 0,5 = 5
Покажем, как можно применять данное правило:
4 1/6 •16 1/6 = (4•64) 1/6 = 64 1/6 = 2
0,5 1,5 •50 1,5 = (0,5•50) 1,5 = 25 1,5 = 25 1+0,5 = 25 1 •25 0,5 = 25•5 = 125
4,9 0,5 •10 0,5 = (4,9•10) 0,5 = 49 0,5 =7
Это правило можно применять следующим образом:
360 0,5 :10 0,5 = (360:10) 0,5 = 36 0,5 = 6
500 3 :50 3 = (500:50) 3 = 10 3 = 1000
6,25 1/4 :0,01 1/4 = (6,25:0,01) 1/4 = 625 1/4 = 5
Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если
то верное и обратное:
То есть любое выражение с корнями в виде степени с рациональным показателем.
Пример. Вычислите значение выражения
Решение. Корней много, поэтому для удобства заменим их степенями
Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:
(9 1/4 ) 1/5 •3 9/10 = (9 0,25 ) 0,2 •3 0,9 = 9 0,25•0,2 •3 0,9 = 9 0,05 •3 0,9 = (3 2 ) 0,05 •3 0,9 =
=3 2•0,05 •3 0,9 = 3 0,1 •3 0,9 = 3 0,1•0,9 = 3 1 = 3
Пример. Упростите выражение
(81 n+1 – 65•81 n ) 0,25
Решение. Степень 81 n+1 можно представить как произведение:
81 n+1 = 81 n •81 1 = 81•81 n
С учетом этого можно записать:
(81 n+1 – 65•81 n ) 0,25 = (81•81 n – 65•81 n ) 0,25 = (81 n (81 – 65)) 0,25 =
= (81 n •16) 0,25 = 81 0,25 n •16 0,25 = 81 0,25 n •16 1/4 = 2•81 0,25 n
Сравнение степеней
Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:
Отсюда следует вывод, что если a 1/ n 1/ n
теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:
Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):
В частности, справедливы следующие неравенства:
Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:
Пример. Сравните выражения с рациональным показателем степени:
20 –3,14 и 50 –3,14
Решение. Избавимся от знака минус в показателе:
20 –3,14 = (1/20) 3,14 = 0,05 3,14
50 –3,14 = (1/50) 3,14 = 0,02 3,14
Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 3,14 3,14
Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 0 0 не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:
18,3546 0 = 12,3647 0 = 1
Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.
На основании этого правила можно записать, что:
Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:
1 –7,56 = 1 –0,15 = 1 0,236 = 1 521,36 = 1
0,5 = 1/2 = 1/(2 1 ) = 2 –1
0,5 7,6 = (2 –1 ) 7,6 = 2 –7,6
0,5 8,9 = (2 –1 ) 8,9 = 2 –8,9
Такие числа мы уже умеем сравнивать. Так как
Например, справедливы неравенства:
0,57 15,36 > 0,57 16,47
Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.
Пример. Докажите, что
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3
Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.
Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 1/3 :
Также ясно, что 27 1/3 1/3 (правило 1). Усилим исходное неравенство:
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 (1)
Действительно, если (1) справедливо, то мы можем записать двойное неравенство
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 1/3
Опустив здесь среднюю часть, получим исходное неравенство. Так как 27 1/3 = 3, мы можем переписать (1) так:
0,9 0,9 + 0,8 0,8 + 0,7 0,7 0,8 0,8 (снова используем правило 1). С другой стороны, 0,9 0,8 0,7 (правило 3). Значит, можно записать двойное неравенство:
Их левые части стоят в (2). Следовательно, можно усилить (2):
0,9 0,7 + 0,9 0,7 + 0,9 0,7 0,7 0,7 0,7 :
Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.
Онлайн-курсы по математике помогут подготовиться к ОГЭ наилучшим образом
Какие возможны действия со степенями?
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Степень, свойства и действия со степенями, сложение, умножение, деление отрицательных степеней, степень с натуральным показателем, правила и формулы
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом: an = a * a * a * …an.
Причем, левая часть уравнения будет читаться, как a в степ. n.
Например:
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
Проверим на примерах:
Как видим, правила работают.
А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
Как производить вычисления в более сложных случаях? Порядок тот же:
Есть специфические свойства, характерные не для всех степеней:
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается:
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
Кроме того, если (-a)2n+2, n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот. Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: Am/n. Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
В этом случае наоборот: Аr2 ˂ Аα ˂ Аr1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.
Ответ: 23·(42−12)=32.
Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Возведение в степень
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136.
Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
Если разделить 134 на 132, то нам потребуется вычислить дробь вида:
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так: am / an = a(m – n).
Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так: (am)n = a(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь: 154 / 154.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150.
Следовательно: 154 / 154 = 150 = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так: a0 = 1.
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка.
Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат.
Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как: a(m/n) есть корень n-ной степени из am. Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции.
Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.