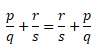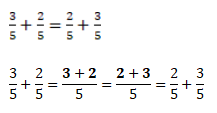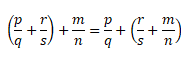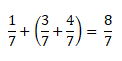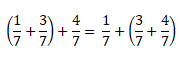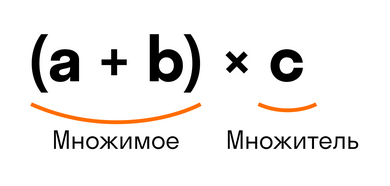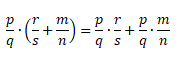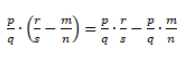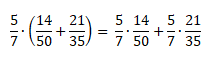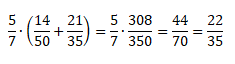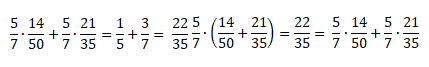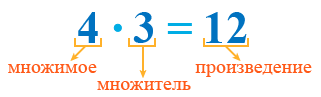Сумма умножения как называется
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 51. Названия компонентов и результата действия умножения
Перечень вопросов, рассматриваемых в теме:
— Связь умножения со сложением, умение заменять сумму одинаковых слагаемых произведением и произведение – суммой одинаковых слагаемых
Умножение – математическое действие, посредством которого из двух чисел получается новое число, которое содержит слагаемым первое число столько раз, сколько единиц во втором.
Произведение – это результат умножения.
Основная и дополнительная литература по теме урока:
8-е изд. – М.: Просвещение, 2017. – с.54.
7-е изд., дораб. – М.: Просвещение, 2016. – с.46.
Открытые электронные ресурсы по теме урока:
Теоретический материал для самостоятельного изучения
Составьте выражения к рисункам:
2 
Учимся рассуждать. Числа разные: 2 и 3.
К данному рисунку можем составить выражение на сложение: 2 + 3 = 5
Числа одинаковые: 2, 2, 2. К данному рисунку можем составить выражение на умножение:
Компоненты каждого математического действия имеют название.
Компоненты сложения указывают на производимое действие – сложение: первое слагаемое, второе слагаемое, сумма.
Названия носят города и реки,
Вам от рождения фамилия дана.
И каждому числу при умножении
Особенные дали имена.
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название.
Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Зная, как называются числа при умножении, можно использовать эти термины при чтении выражений.
Равенство 5 · 2 = 10 можно прочитать несколькими способами:
— Первый множитель – пять, второй множитель – два, произведение – десять.
— Произведение пяти и двух равно десяти.
— Пять умножить на два, равняется десять.
Рассмотрим задание: слагаемое 12 повторяется 4 раза. Запишите такую сумму в виде произведения.
Назовите первый множитель этого произведения. Что он обозначает?
Первый множитель этого произведения обозначает слагаемое.
Слагаемое 12 повторяется 4 раза.
Назовите второй множитель этого произведения. Что он обозначает? Второй множитель этого произведения обозначает количество слагаемых.
Слагаемое 12 повторяется 4 раза.
Получилась запись: 12+12+12+12=12·4
Помните, что заменить сложение умножением можно там, где находятся суммы одинаковых слагаемых.
1. Запишите пример на умножение там, где это возможно:
Законы математики
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Переместительный закон сложения
Начнем изучать основные законы математики со сложения натуральных чисел.
Переместительный закон сложения
От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:
m + n = n + m
Переместительный закон сложения работает для любых чисел.
Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.
Приведем пример с весами, которые используют продавцы в магазинах.
Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.
При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.
Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:
Формула переместительного закона для обыкновенных дробей:
Чтобы сложить две дроби с одинаковым знаменателем, нужно сложить числители, а знаменатель оставить прежним. Вот так:
Сочетательный закон сложения
Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.
Сочетательный закон сложения: два способа
Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.
Рассмотрим сумму из трех слагаемых:
Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:
Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:
В обоих случаях получается один и тот же результат — что и требовалось доказать.
Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:
Отразим сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Формула сочетательного закона для обыкновенных дробей:
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.
Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.
Значит, сочетательный закон справедлив и для обыкновенных дробей.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Переместительный закон умножения
С каждым новым правилом решать задачки по математике все интереснее.
Переместительный закон умножения
От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.
Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:
В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.
Переместительный закон умножения с помощью переменных выглядит так:
a * b = b * a
Сочетательный закон умножения
Рассмотрим еще один полезный закон в математике.
Сочетательный закон умножения
Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.
Другими словами, умножайте числа в любом порядке — как вам больше нравится.
Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:
А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:
Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.
Для любых натуральных чисел a, b и c верно равенство:
a * b * с = (a * b) * с = a * (b * с)
Пример
Вычислить: 5 * 6 * 7 * 8.
Это выражение можно вычислять в любом порядке. Вычислим слева направо:
Распределительный закон умножения
Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:
Распределительный закон умножения
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:
Сначала выполним действие в скобках:
В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:
Отразим распределительный закон умножения с помощью переменных:
(a + b) * c = a * c + b * c
Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:
c * (a + b) = c * a + c * b
Пример 1
Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:
5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25
Пример 2
Найти значение выражения 2 * (5 + 2).
Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:
2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14
Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.
Пример 3
Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:
4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16
Распределительный закон умножения для суммы обыкновенных дробей:
Распределительный закон умножения для разности обыкновенных дробей:
Проверим справедливость этого закона:
Посчитаем, чему равна левая часть равенства.
Теперь посчитаем, чему равна правая часть равенства.
Так мы доказали справедливость распределительного закона.
Задания для самопроверки
Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂
Задание 1. Найти значение выражения: 8 * (1 + 6).
Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).
Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).
Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).
Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
Числа при умножении
Результат умножения, или Произведение
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
Заменяем сложение умножением и получаем:
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Умножение, сложение, вычитание и деление целых чисел: основные свойства
Сложение целых чисел. Основные свойства
Коммутативное свойство сложения
Переместительное (коммутативное свойство) или переместительный закон.
От перемены мест слагаемых сумма не меняется.
Согласно этому свойству, справедливо равенство:
Свойство коммутативности работает вне зависимости от знака.
Ассоциативное свойство сложения
Сочетательное (ассоциативное свойство) или сочетательный закон.
Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.
a + b + c = a + b + c
Примечание: данное свойство применимо и для большего количества слагаемых.
Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:
Свойства сложения, связанные с числом 0
Прибавление нуля к любому целому числу не меняет этого числа.
2. Сумма любого целого числа и противоположного ему числа равна нулю.
Умножение целых чисел. Основные свойства
Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.
Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.
Переместительное свойство умножения
От перемены мест множителей произведение не меняется.
Сочетательное свойство умножения
Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:
a · ( b · c ) = ( a · b ) · c
Примечание: данное свойство применимо и для большего количества множителей.
В соответствии с этим свойством можно говорить о справедливости следующих равенств:
Умножение числа на нуль
Результатом умножения любого целого числа на нуль является число нуль.
Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.
Умножение числа на единицу
Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.
a · ( b + c ) = a · b + a · c
Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.
В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.
Вычитание целых чисел. Основные свойства
Основные свойства вычитания
Деление целых чисел. Основные свойства
Умножение натуральных чисел
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Сократим запись, заменив сложение на умножение:
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.