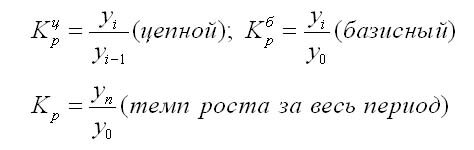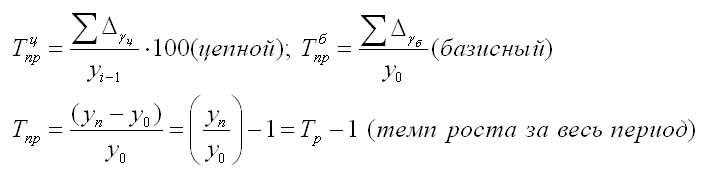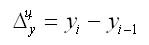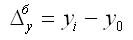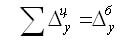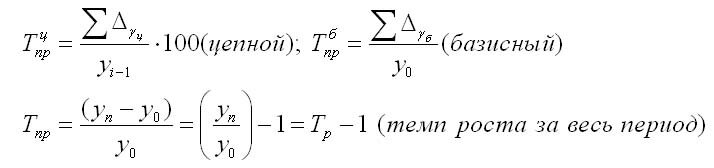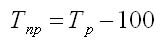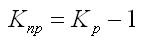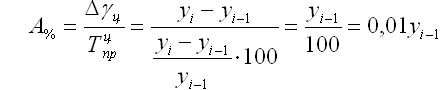Темпы динамики вычисляются как
Показатели динамики: темп роста и темп прироста
Темп роста
Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.
Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста может быть рассчитан по формулам:
Также темп роста может определяться так:
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.
Абсолютный прирост
Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:
1. Абсолютный прирост (цепной):
2. Абсолютный прирост (базисный):
где уi — уровень сравниваемого периода;
Уi-1 — Уровень предшествующего периода;
У0 — уровень базисного периода.
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:
Темп прироста можно получить из темпа роста:
Коэффициент прироста может быть получен таким образом:
Абсолютное значение 1%-го прироста
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.
Примеры расчетов показателей динамики
Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики
О показателях динамики
При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.
Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.
Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.
13 Ряды динамики
Статистическое изучение динамики социально-экономических явлений
Процессы и явления социально-экономической жизни общества, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Для того, чтобы выявить тенденции и закономерности социально-экономического развития явлений, статистика строит особые ряды статистических показателей, которые называются рядами динамики (иногда их называют временными рядами), то есть ‑ это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В англоязычной литературе для временных рядов используется термин «time series». Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.
Каждый ряд динамики характеризуется двумя параметрами: значениями времени и соответствующими им значениями уровней ряда. Уровни ряда обычно обозначаются «yt»: y1, y2 и т.д. В качестве показателя времени в рядах динамики могут указываться отдельные периоды (сутки, месяцы, кварталы, годы и т.д.) времени или определенные моменты (даты). Время в рядах динамики обозначается через «t».
Ряд динамики состоит из двух элементов:
1) уровня ряда (значения изучаемого показателя);
2) моментов (периодов) времени, когда фиксируется этот показатель.
Основные способы обработки рядов динамики:
1) укрупнение интервалов и расчет для них средних показателей;
2) сглаживание уровней способом скользящей средней;
3) выравнивание по аналитическим формулам.
Суть последнего способа заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени.
Ряды динамики, как правило, представляют в виде таблицы или графически.
Ряды динамики могут быть классифицированы по следующим признакам:
В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин ‑ как производные.
Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.
Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.
Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.
В зависимости от характера временного параметра ряды динамики делятся на моментные и интервальные.
Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени.
Пример. Моментный ряд динамики, характеризующий численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г., представлен в таблице 13.1.
Таблица 13.1 ‑ Численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 |
| Численность персонала, чел. | 780 | 810 | 880 | 930 | 940 | 970 |
Следует помнить, что моментные ряды абсолютных величин нельзя суммировать. Бессмысленно, например, складывать численность персонала по состоянию на 1 января, 1 февраля и т.д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же единицы совокупности.
Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным.
Пример. Интервальный ряд динамики, представлен в таблице 13.2.
Таблица 13.2. ‑ Характеристика динамики объема розничного товарооборота
| Дата | 2004 | 2005 | 2006 | 2007 | 2008 |
| Товарооборот, млн. руб. | 28,3 | 31,9 | 38,3 | 42,3 | 45,2 |
Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда вполне реальный показатель, например, общий объем розничного товарооборота за 2004-2008 г.г.
В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и не равноотстоящими уровнями во времени.
Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими, пример (табл. 13.1 и табл. 13.2).
Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими, пример(табл. 13.3).
Пример. Рядом динамики с не равноотстоящими уровнями во времени может служить объем экспорта продукции предприятия, представленный в таблице 13.3.
Таблица 13.3. – Динамика объема экспорта продукции предприятия
| Годы | 1993 | 1996 | 1998 | 2000 | 2004 |
| Объем экспорта, млн. долл. | 1110 | 1220 | 1320 | 1450 | 1640 |
По числу показателей можно выделить изолированные (одномерные) и комплексные (многомерные) ряды динамики.
Если ведется анализ во времени одного показателя ряда, то ряд динамики изолированный (например, данные о производстве газа по годам). В многомерном ряду представлена динамика нескольких показателей, характеризующих одно явление.
Сопоставимость уровней и смыкание рядов динамики
Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Рассмотрим основные причины несопоставимости уровней ряда динамики.
Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета.
Пример. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие ‑ в квадратных метрах.
На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.
Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие ‑ с убранной, то такие уровни будут несопоставимы.
В процессе развития во времени, прежде всего, происходят количественные измерения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.
Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл.
Например, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных границ областей, районов и так далее.
Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
Пример. Предположим, что в N-ом регионе имеются данные об общем объеме оборота розничной торговли за 2013-2015 гг. в фактически действующих ценах, и за 2015-2018 гг. ‑ в сопоставимых ценах (табл. 13.4.).
Таблица 13.4 ‑ Динамика общего объема оборота розничной торговли (млрд. руб.) цифры условные
Показатели рядов динамики: их вычисление и прогнозирование
Различные экономические и другие показатели, которые даны за определённый период времени или по состоянию на некоторый момент, широко используются в практической статистике. Информация, основанная на этих показателях, называется рядами динамики. Абсолютные значения исследуемого явления в ряде динамики по состоянию на соответствующий период времени или момент называются уровнями ряда динамики. На их основе вычисляются важнейшие показатели рядов динамики и в математическом плане нужно лишь складывать, вычитать, делить, умножать и извлекать корень, а также помнить, что нельзя менять хронологическую последовательность уровней ряда динамики. А ещё на основе уже зафиксированных уровней ряда динамики можно прогнозировать значения уровней для будущих периодов и здесь уже начинается «взрослая» математика.
Цепные и базисные показатели рядов динамики и их вычисление
Главными показателями, характеризующими абсолютные и относительные изменения рядов динамики являются: абсолютный прирост (снижение), темп роста, темп роста, темп прироста, абсолютное значение одного процента прироста (снижения).
Показатели рядов динамики по характеру их вычисления делятся на цепные и базисные.
Базисные показатели вычисляют, сравнивая каждый уровень ряда динамики с одним и тем же уровнем, принятым за базис. Обычно это первый (начальный) уровень ряда, хотя, если это продиктовано задачей анализа, за базисный уровень можно принять любой другой уровень. Если начальный уровень ряда динамики для изучаемого явления или процесса представляет нетипично высокий или нетипично низкий, то рассчитанные по сравнению с ним показатели рядов динамики могут оказаться мало полезными для задачи анализа.
Введём следующие обозначения:
Будем рассчитывать показатели для ряда динамики, данного в следующей таблице:
Таблица. Объёмы экспорта предприятия «Х», в миллионах руб.
Цепной абсолютный прирост (снижение) вычисляется путём вычитания из какого-либо уровня ряда динамики предыдущего уровня того же ряда.
Пример 1. Вычислим цепной абсолютный прирост:
Общий объём экспорта предприятия «Х» с 2013 по 2017 годы составляет Δ ц ( 2014 ) + Δ ц ( 2015 ) + Δ ц ( 2016 ) + Δ ц ( 2017 ) = 1631,8 млн. руб.
Базисный абсолютный прирост вычисляется путём вычитания из какого-либо уровня ряда динамики начального уровня ряда, который принимается за базис.
Пример 2. Вычислим базисный абсолютный прирост:
Между цепным и базисным абсолютным приростами существует математическая взаимосвязь: сумма цепных абсолютных приростов (снижений) равна базисному абсолютному приросту (снижению), соответствующему последнему уровню ряда динамики:
Показатель интенсивности изменения ряда динамики, в зависимости от того, выражен он в виде коэффициента или в процентах, называется коэффициентом роста или темпом роста.
Коэффициент роста показывает, во сколько раз соответствующий уровень ряда динамики больше базисного уровня (если коэффициент больше единицы) или какую часть базисного уровня представляет уровень отчётного периода (если он меньше единицы).
Темп роста характеризует скорость развития исследуемого явления.
Коэффициент роста × 100 = темп роста, %.
Если абсолютные уровни исследуемого явления снижаются, то темп роста меньше единицы (меньше 100 %), однако он никогда не может быть отрицательным числом. Существуют цепные и базисные темпы роста. Цепной темп роста вычисляется путём деления уровня ряда динамики на предыдущий уровень ряда:
Общий темп роста за весь период вычисляется путём умножения всех темпов роста:
Пример 3. Вычислим цепные темпы роста:
Общий темп роста за весь период:
Базисный темп роста вычисляют путём деления какого-либо уровня ряда динамики на начальный уровень, который считают базисным:
Пример 4. Вычислим базисные темпы роста:
Между цепным и базисным темпами роста существует математическая взаимосвязь: произведение цепных темпов роста равно базисному темпу роста для последнего уровня ряда динамики:
Таким образом, формулы для вычисления коэффициента прироста:
K пр ( ц ) = T р ( ц ) − 1
Формулы для вычисления темпа прироста:
T пр ( ц ) = T р ( ц ) − 100 %
В отличие от темпов роста, темпы прироста могут быть и отрицательными числами. В этом случае они показывают, на какую часть целого или на сколько процентов снизился уровень исследуемого явления.
Между цепным и базисным темпами прироста нет математической взаимосвязи.
Средние значения показателей рядов динамики
Средние значения показателей рядов динамики выражают уровни и типичные значения их изменений в определённый период времени. Прежде чем рассматривать средние значения показателей рядов динамики, разграничим понятия интервальных и моментных рядов динамики.
Интервальные ряды динамики характеризуют значения изучаемого явления за некоторый период времени, например, за месяц, за год, за пять лет. Моментные ряды динамики характеризуют значения изучаемого явления в какой-то определённый момент времени, например, на начало или конец месяца, начало или конец года и так далее. В предыдущем параграфе мы рассматривали интервальный ряд динамики и его показатели.
Средний уровень интервального ряда динамики вычисляется путём деления суммы уровней ряда на число уровней:
Пример 5. Вычислить среднегодовой объём экспорта предприятия «Х».
Решение. Вычислим средний уровень по формуле для интервального ряда динамики:
Пример 6. Вычислить среднее число сотрудников предприятия «Х» на начало года. В таблице ниже даны значения числа сотрудников на начало каждого года с 2013 по 2017 годы.
| Момент | Число |
| 1 янв. 2013 | 1113 |
| 1 янв. 2014 | 1122 |
| 1 янв. 2015 | 1110 |
| 1 янв. 2016 | 1130 |
| 1 янв. 2017 | 1222 |
Решение. Вычисляем по формуле хронологической средней:
Средний абсолютный прирост (снижение) выражает абсолютную величину, на которую в среднем в каждую единицу времени в соответствующий период выросли или снизились показатели исследуемого явления. Его вычисляют путём деления суммы цепных абсолютных приростов на число абсолютных приростов:
где 
Если нет данных о цепных абсолютных приростах, но известны начальный и конечный уровни ряда динамики, то средний абсолютный прирост можно вычислить через базовый абсолютный прирост по формуле
Пример 7. Используя данные об экспорте предприятия «Х», вычислить среднегодовой прирост экспорта.
Решение. Вычислим интересующий нас показатель через сумму цепных абсолютных приростов:
Вычислим его же через базовый абсолютный прирост:
Как видим, получили один и тот же результат.
Средний темп роста является показателем изменения интенсивности изменения уровней ряда динамики. Он характеризует среднюю интенсивность развития исследуемого явления, показывая, во сколько раз в среднем в единицу времени изменились уровни ряда динамики. Средний темп роста можно выразить в коэффициентах или процентах.
Цепной средний темп роста вычисляется по формуле среднего геометрического:
Если нет информации о каждом цепном темпе роста, средний темп роста можно вычислить по формуле с использованием последнего и первого уровней ряда динамики
Пример 8. Вычислить средний темп роста экспорта предприятия «Х».
Решение. Вычисляем по формуле среднего геометрического:
Вычисляем по формуле с использованием последнего и первого уровней ряда динамики:
Получили один и тот же результат.
Средний темп прироста показывает, на сколько процентов в среднем увеличился (если он со знаком «плюс») или уменьшился (если со знаком «минус») уровень исследуемого явления в течение всего рассматриваемого периода. Средний темп прироста вычисляется путём вычитания из среднего темпа роста 100% (если он выражен в процентах) или единицы (если он выражен в виде коэффициента).
Прогнозирование уровней рядов динамики
Модели на основе средних значений могут быть использованы, когда значение уровня ряда динамики колеблется вокруг среднего значения и в ряде нет какой-либо ярко выраженной тенденции (тренда).
Метод скользящей средней
В прогнозировании значение скользящей средней (обозначим её M t ) вычисляется по формуле
Пример 9. Рассмотрим пример с данными об объёмах продаж холодильников предприятия «Х» по месяцам.
При рассмотрении графика объёма продаж видно, что изменения объёма не подвержены какой-либо долгосрочной тенденции или тренду, объёмы продаж колеблются вокруг среднего значения.
Поэтому при расчёте прогноза можно использовать среднее значение. Вычислим значения скользящей средней по приведённой выше формуле:
Результаты даны в третьем столбце таблицы (для первых двух месяцев по этой формуле скользящие средние вычислить невозможно).
| Месяцы t | Объёмы продажи холодильников y t | Скользящая средняя M t |
| 1 | 113 | — |
| 2 | 117 | — |
| 3 | 112 | 114 |
| 4 | 113 | 114 |
| 5 | 108 | 111 |
| 6 | 112 | 111 |
| 7 | 116 | 112 |
| 8 | 120 | 116 |
| 9 | 121 | 119 |
| 10 | 113 | 118 |
| 11 | 111 | 115 |
| 12 | 118 | 114 |
| Прогноз F t | Погрешность прогноза ε t |
| — | — |
| — | — |
| — | — |
| 114 | -1 |
| 114 | -6 |
| 111 | 1 |
| 111 | 5 |
| 112 | 8 |
| 116 | 5 |
| 119 | -6 |
| 118 | -7 |
| 115 | 3 |
Наиболее вероятные прогнозы на каждый месяц по соответствующей формуле даны в четвёртом столбце таблицы. Прогноз на первый месяц следующего года F 13 = 114 можно сделать по данным трёх последних месяцев.
Погрешность прогноза для каждого момента времени вычисляется по формуле
Среднюю погрешность прогноза на основе скользящей средней обычно вычисляется как среднее абсолютное отклонение, которое обозначается MAD (Mean Absolute Deviation):
При оценке прогноза можно использовать также среднюю квадратическую погрешность и среднюю абсолютную процентную ошибку.
Средняя квадратическая погрешность MSE (Mean Squared Error) вычисляется по формуле
Средняя абсолютная процентная ошибка MAPE (Mean Absolute Percenting Error) вычисляется по формуле
Пример 10. В нашем случае, когда N=3, MAD=4,67. Для значений N от 2 до 6 значения MAD следующие:
| N | MAD |
| 2 | 4,50 |
| 3 | 4,67 |
| 4 | 4,78 |
| 5 | 4,11 |
| 6 | 4,42 |
На основе этих значений погрешности можем сделать вывод, что при использовании интервала сглаживания длиной в пять периодов можно получить наилучший прогноз с точки зрения минимального среднего абсолютного отклонения. С использованием такого интервала сглаживания получаем прогноз: наиболее вероятно, что в первый месяц следующего года будут проданы 116 холодильников:
При использовании формулы значения скользящей средней каждому уровню ряда динамики в границах периода сглаживания присваивается один и тот же вес. Так, если N=3, то вес соответствует 1/3, поэтому формулу в этом случае можно записать так:
Модели прогнозирования на основе скользящей средней и скользящей средневзвешенной имеют существенный недостаток: для вычисления пронозируемого значения используются только последние N уровней ряда динамики и только для вычисления погрешности используются предыдущие n − N уровней. Поэтому для прогнозирования средних значений рядов динамики используются и другие методы.
Метод экспоненциальной средней (экспоненциального сглаживания)
Основная формула значения экспоненциальной средней:
Таким образом, прогноз для каждого следующего периода строится на среднем взвешенном значении предыдущего уровня ряда динамики и значении предыдущего прогноза. Например, для прогноза значения четвёртого уровня ряда динамики формула будет следующей:
для прогноза третьего уровня
для прогноза второго уровня
В общем случае прогноз на каждый следующий период является средней взвешенной величиной от всех предыдущих уровней ряда динамики.
Вернёмся к уравнениям прогноза значений третьего и четвёртого уровней ряда динамики. Подставляя каждое следующее уравнение в предыдущее, получаем
Таким образом, в общем случае прогнозируемое значение вычисляется с использованием всех уровней ряда динамики путём их умножения на соответствующие коэффициенты (весы): 

В зависимости от величины параметра экспоненциального сглаживания α различным уровням ряда динамики можно присвоить различные весы. Например, если о прогнозируемом показателе известно, что на его будущие значения больше влияют более близкие из предыдущих уровней ряда, то параметр α должен быть больше, чем в случае, когда бОльшее влияние оказывают более ранние значения ряда динамики. А если бОльшее влияние оказывают более ранние значения, то параметр α должен быть меньше.
Пример 11. Сделаем прогноз методом экспоненциального сглаживания для ряда динамики, содержащего данные об объёмах продажи холодильников предприятия «Х» из предыдущих примеров.
F 2 = 0,2⋅113 + (1 − 0,2)⋅113,0 = 113,0
F 3 = 0,2⋅117 + (1 − 0,2)⋅113,0 = 113,8
F 4 = 0,2⋅112 + (1 − 0,2)⋅113,8 = 113,44
Прогноз на первый месяц следующего года:
| Месяцы t | Объёмы продажи холодильников y t |
| 1 | 113 |
| 2 | 117 |
| 3 | 112 |
| 4 | 113 |
| 5 | 108 |
| 6 | 112 |
| 7 | 116 |
| 8 | 120 |
| 9 | 121 |
| 10 | 113 |
| 11 | 111 |
| 12 | 118 |
| Прогноз ( α = 0,2 ) F t | Погрешность прогноза ε t |
| 113,0 | 0 |
| 113,0 | 4 |
| 113,8 | -1,8 |
| 113,44 | -0,44 |
| 114,35 | -6,35 |
| 112,28 | -0,28 |
| 112,23 | 3,77 |
| 112,98 | 7,02 |
| 114,38 | 6,62 |
| 115,71 | -2,71 |
| 115,17 | -4,17 |
| 114,33 | 3,67 |
| α | MSE |
| 0,01 | 4,01 |
| 0,02 | 4,00 |
| 0,05 | 3,97 |
| 0,10 | 3,97 |
| 0,15 | 3,98 |
| 0,20 | 4,02 |
| 0,25 | 4,05 |
| 0,30 | 4,08 |
| 0,35 | 4,13 |
| 0,40 | 4,16 |
| 0,45 | 4,20 |
| 0,50 | 4,23 |
Видим, что наименьшая погрешность прогноза для данного ряда динамики при использовании метода экспоненциального выравнивания соответствует значениям α от 0,05 до 0,15. Примем за оптимальное значение в середине между этими двумя, то есть 0,1. Тогда получим следующий прогноз объёма продаж: 114,3.
Формулу экспоненциальной средней можно преобразовать, чтобы в прогнозе учитывалась погрешность прогноза для предыдущего периода:
Как показывает последнее выражение, прогноз по методу экспоненциальной средней образуется из прогноза с экспоненциальным средним значением прошлого периода с прибавлением погрешности ошибки, умноженной на параметр сглаживания α. Если погрешность больше нуля, это означает, что предыдущий прогноз был меньше фактического значения и следующий прогноз будет соответственно увеличен. Если погрешность меньше нуля, то прогноз был меньше фактического значения и прогноз на следующий период будет соответственно уменьшен.