Теорема косинусов как решать
Теорема косинусов (ЕГЭ 2022)
Что же такое теорема косинусов?
Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт!
Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов 🙂
Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу!
Теорема косинусов — коротко о главном
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Почему теорема косинусов это… теорема Пифагора
И причем тут теорема Пифагора? Сейчас поясню.
Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
А что будет, если угол \( \displaystyle \angle C\), скажем, острый?
Вроде ясно, что величина \( \displaystyle <
А если угол \( \displaystyle \angle C\) – тупой?
Ну, тогда величина \( \displaystyle <
Но, опять же, на сколько? И как это связано с величиной \( \displaystyle \angle C\)?
Обрати внимание на вот эту добавку к теорему Пифагора: \( \displaystyle «-2ab\cos \gamma »\).
Вот она и «адаптирует» теорему Пифагора под острые и тупые углы треугольника. Сейчас мы докажем теорему косинусов и ты увидишь в теореме косинусов теорему Пифагора своими глазами.
Доказательство теоремы косинусов
Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов.
Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Рассмотрим три случая:
И убедимся, что для всех трех случаев теорема косинусов работает!
Угол С острый
\( \displaystyle \angle C
Он прямоугольный, можно пользоваться теоремой Пифагора:
\( \displaystyle AH\) можно выразить из треугольника (прямоугольного!) \( \displaystyle AHC\).
\( \displaystyle AH=b\sin \gamma \)
А вот \( \displaystyle BH=a-CH=a-b\cos \gamma \) (снова из \( \displaystyle \Delta AHC\) ).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Угол С тупой
Начинаем точно также: опускаем высоту из точки \( \displaystyle A\).
А теперь, внимание, отличие!
\( \displaystyle BH=a+b\cos \left( <<180>^<\circ >>-\gamma \right)\).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Угол С прямой
Но тогда \( \displaystyle \cos \gamma =0\) и теорема косинусов просто превращается в теорему Пифагора:
В каких же задачах бывает полезна теорема косинусов?
Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону.
Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле:
И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба.
Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора.
И приходи к нам на бесплатные вебинары и занятия ( о них ниже).
Бонус: Вебинар на решение задач по теореме косинусов и синусов
Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части.
Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
Теорема косинусов
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
Длина третьей стороны — примерно 17,436 см.
Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.
2. Вычитаем это из стороны b, так мы получим DA:
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
Используем формулу теоремы косинусов
Подставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
Теорема синусов
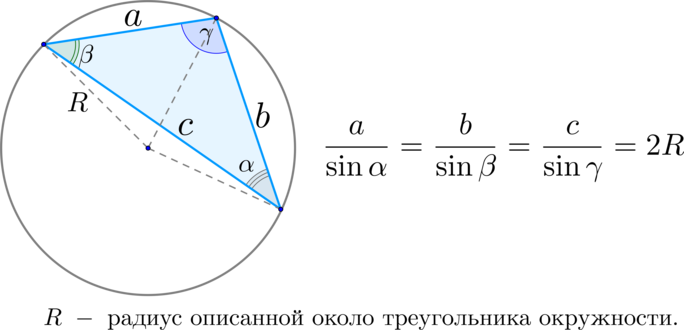
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:
Теорема косинусов
Формулировка теоремы косинусов
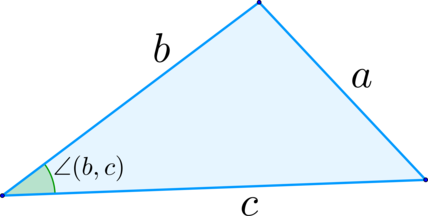
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
| Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними |
Полезные формулы теоремы косинусов:
Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов.
Теорема Пифагора
Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5).
Поэтому справедливо равенство
что и требовалось доказать.
Формулировка теоремы косинусов для треугольника
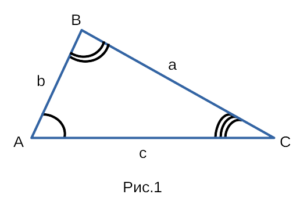
Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами 
, 
, и 
длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.
Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:
На рисунке для удобства дальнейших рассуждений угол С обозначен углом 
. Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
Понятно, что если бы вы выражали другую сторону треугольника, например, сторону , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны и . Выражение для квадрата стороны . Выражение для квадрата стороны получается аналогично:
Классическое доказательство теоремы косинусов.
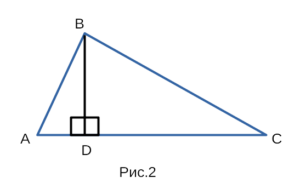
Пусть есть треугольник ABC. Из вершины C на сторону AB опустили высоту CD. Значит:
Записываем теорему Пифагора для 2-х прямоугольных треугольников ADC и BDC:
h 2 = b 2 – (b cos α) 2 (1)
h 2 = a 2 – (c – b cos α) 2 (2)
Приравниваем правые части уравнений (1) и (2):
b 2 – (b cos α) 2 = a 2 – (c – b cos α) 2
a 2 = b 2 + c 2 – 2bc cos α.
Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определить стороны b и c:
b 2 = a 2 + c 2 – 2ac cos β
c 2 = a 2 + b 2 – 2ab cos γ.
Формулировка и формула теоремы
В плоском треугольнике квадрат стороны равняется сумме квадратов двух других сторон минус удвоенное произведение данных сторон, умноженное на косинус угла между ними.
a 2 = b 2 + c 2 – 2bc cos α
Теорема косинусов для остроугольного треугольника.
Если угол острый, то справедлива формула:
Доказательство теоремы косинусов для треугольника
Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.
Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь.
Заменим стороны нашего треугольника следующими векторами:
Согласно правилам сложения векторов имеем: 
. Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим 
. Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение: 
.
Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим:
Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов:
Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост 
. Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
Теорема косинусов
Докажем, что длины сторон этого треугольника удовлетворяют равенству
| a 2 = b 2 + c 2 – – 2bc cos A | (1) |
С этой целью проведём высоту BD из вершины B (рис.7).
В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства
BD = c sin A, AD = c cos A, DC = b – AD = b – c cos A.
Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана.
откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов.
Примеры задач
Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.
Задание 2
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.
Решение:
Примем бОльшую сторону за a. Чтобы найти угол между сторонами b и c, воспользуемся следствием из теоремы:
Следовательно, угол α = arccos (-1/6) ≈ 99,59°.
Теорема косинусов для прямоугольного треугольника
Теорема косинусов для прямоугольного треугольника.
Рассмотрим прямоугольный треугольник ABC:
По теореме косинусов сторона «а» равна:
но угол А прямой, косинус прямого угла равен нулю, отсюда получаем:
Таким образом мы получили формулу теоремы Пифагора:
Теорема косинусов
Чтобы найти строну или угол треугольника применяют Теорему Косинусов.
Эта теорема обобщает теорему Пифагора. Доказать Теорему
Косинусов достаточно просто через треугольник, который
разделяют высотой на два прямоугольных треугольника.
Мы рассмотрим доказательство, формулировку,
следствия из Теоремы Косинусов.
Наряду с одной из известных теорем геометрии — теоремой Пифагора,
существует теорема косинусов. Теорема косинусов похожа по теорему
Пифагора, но отличается. Теорему косинусов, можно применить к абсолютно
любым треугольникам. А теорема Пифагора применяется исключительно
для прямоугольных треугольников.
Теорема косинусов — это теорема геометрии, обобщающая
теорему Пифагора, применяющаяся при нахождении углов
и сторон в любых треугольниках.
Формулировка теоремы косинусов
Формулировка у теоремы косинусов такая: в треугольнике квадрат любой из сторон
равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними. Запишем эту
формулировку более кратко, используя рисунок 1, на котором изображен
произвольный треугольник ABC: \( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A \) .
Или, же еще более кратко: \( a^2 = b^2 + c^2 — 2bc * cos ∠A \) .
Доказательство теоремы косинусов
Для доказательства теоремы косинусов воспользуемся
рисунком 2, на котором изображен треугольник ABC.
Докажем, что \( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A: \)
Следствия из теоремы косинусов
Значение теоремы косинусов
Где применяется теорема косинусов?
Теорема косинусов применяется в тригонометрии, в частности
при нахождение сторон и углов в любых треугольниках. Например, зная
формулировку теоремы косинусов, косинус одно из угла треугольника,
и две стороны можно найти неизвестную сторону треугольника.
Виды теорем косинусов.
В зависимости от свойств треугольника, длины его сторон, градусной меры
его углов — теорема косинусов немного видоизменяется. Например, в
прямоугольных треугольниках теорема косинусов преобразуется в теорему Пифагора.
Теорема синусов и теорема косинусов
\(\blacktriangleright\) Теорема синусов:
\(\blacktriangleright\) Теорема косинусов: \(\Large
Выпускники, которые готовятся сдавать ЕГЭ по математике и хотят получить достаточно высокие баллы, обязательно должны освоить принцип решения задач на применение теоремы синусов и косинусов. Многолетняя практика показывает, что подобные задания из раздела «Геометрия на плоскости» являются обязательной частью программы аттестационного испытания. Поэтому, если одним из ваших слабых мест являются задачи на теорему косинусов и синусов, рекомендуем обязательно повторить базовую теорию по данной теме.
Готовьтесь к экзамену вместе с образовательным порталом «Школково»
Занимаясь перед сдачей ЕГЭ, многие выпускники сталкиваются с проблемой поиска базовой теории, необходимой для решения практических задач на применение теоремы синусов и косинусов.
Учебник далеко не всегда оказывается под рукой в нужный момент. А найти необходимые формулы иногда бывает достаточно проблематично даже в Интернете.
Подготовка к аттестационному испытанию вместе с образовательным порталом «Школково» будет максимально качественной и эффективной. Чтобы задачи на теорему синусов и косинусов давались легко, рекомендуем освежить в памяти всю теорию по данной теме. Этот материал наши специалисты подготовили на основе богатого опыта и представили в понятной форме. Найти его вы можете в разделе «Теоретическая справка».
Знание базовых теорем и определений — это половина успеха при прохождении аттестационного испытания. Отточить навык решения примеров позволяют соответствующие упражнения. Чтобы их найти, достаточно перейти в раздел «Каталог» на образовательном сайте «Школково». Там представлен большой перечень заданий различного уровня сложности, который постоянно дополняется и обновляется.
Задачи на теоремы синусов и косинусов, подобные тем, что встречаются в ЕГЭ по математике, учащиеся могут выполнять в онлайн-режиме, находясь в Москве или любом другом российском городе.
В случае необходимости любое упражнение, например, на вычисление синуса угла треугольника, можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему, чтобы еще раз проанализировать алгоритм нахождения правильного ответа и обсудить его с преподавателем в школе или репетитором.