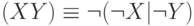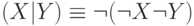Доказать что формулы логически эквивалентны
Эквивалентность формул
Смотреть на youtube || на ИНТУИТ в качестве: низком | среднем | высоком
Одну и ту же функцию можно задать разными формулами. Поэтому возникает задача определения эквивалентности формул логики высказываний.
Давайте установим эквивалентности для некоторых функций из таблицы 3 предыдущего урока.
Исключающее Или эквивалентно отрицанию эквивалентности:
Построим таблицы истинности для этих двух формул:
 |  |  |  |  |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Штрих Шеффера эквивалентен отрицанию конъюнкции:
Построим таблицы истинности для этих двух формул:
 |  |  |  |  |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Операцию Штрих Шеффера называют антиконъюнкцией.
Стрелка Пирса эквивалентна отрицанию дизъюнкции:
Построим таблицы истинности для этих двух формул:
 |  |  |  | 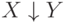 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Операцию Стрелка Пирса называют антидизъюнкцией.
Импликация 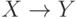


Построим таблицы истинности для этих двух формул:
 |  | 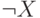 |  | 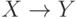 |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
Конъюнкция 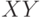
Построим таблицы истинности для этих двух формул:
 |  | 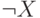 |  |  | 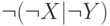 | 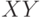 |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
Дизъюнкция 
Построим таблицы истинности для этих двух формул:
 |  | 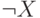 |  | 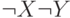 | 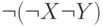 |  |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
Почему на практике используется небольшое число функций?
Логических функций много, особенно функций многих переменных. Почему же мы знаем и оперируем небольшим числом функций? Связано это с тем, что одни функции можно выражать через другие, как мы видели на примерах. А можно ли любую функцию выразить через немногие, базисные функции? Ответ на этот вопрос положителен.
Каждую функцию от любого числа переменных можно представить в так называемой нормальной форме, в которой используются только три базисные функции – отрицание, конъюнкция и дизъюнкция.
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Формулы. Как и в анализе, исходя из элементарных функций, можно строить формулы.
$((x_1x_2) + x_1, ((x_1x_2) + x_1)\rightarrow x_2$
| $x_1$ | $x_2$ | $x_1x_2$ | $(x_1x_2)+x_1$ | $((x_1x_2)+x_1)\rightarrow x_2$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Равенство функций и эквивалентность формул
Введенное понятие функции не позволяет рассматривать функции от меньшего числа аргументов как функции от большего числа аргументов.
$f(\alpha_1. \alpha_ < i-1 >,0,\alpha_ < i+1 >. \alpha_n) \neq f(\alpha_1. \alpha_ < i-1 >,1,\alpha_ < i+1 >. \alpha_n)$.
Далее:
Теорема о заведомо полныx системаx
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
Поток векторного поля через поверхность
Специальные векторные поля
Свойства криволинейного интеграла второго рода
Теорема Остроградского
Условия независимости криволинейного интеграла от пути интегрирования
Логические следствия
Вычисление поверхностного интеграла первого рода
Вычисление объёмов
Примеры применения цилиндрических и сферических координат
Решение задач с помощью алгебры высказываний
MT1102: Линейная алгебра (введение в математику)
Определение
Формулы алгебры высказываний %%X%% и %%Y%% называют равносильными (эквивалентными, тождественными), если при любых значениях переменных, входящих в эти формулы, значение истинности формул %%X%% и %%Y%% совпадают.
Пример
Построим таблицу истинности для этих двух формул
| %%A%% | %%B%% | %%X = A \rightarrow B%% | %%Y = \overline \rightarrow \overline%% |
|---|---|---|---|
| %%0%% | %%0%% | %%1%% | %%1%% |
| %%0%% | %%1%% | %%1%% | %%1%% |
| %%1%% | %%0%% | %%0%% | %%0%% |
| %%1%% | %%1%% | %%1%% | %%1%% |
Как видно из таблицы, истинностные значения данных формул совпадают при любых значениях %%A%% и %%B%%, следовательно, эти две формулы равносильны. Равносильность формул %%X%% и %%Y%% записывается в виде %%X \equiv Y%%.
Теоремы о равносильности формул
Теорема. Справедливы следующие равенства формул.
A \land 0 \equiv 0 \\ A \lor 0 \equiv A,
Где %%1%% — тождественно истиннная формула, а %%0%% — тождественно ложная формула.
Теорема дается без доказательства, так как эти формулы легко проверить, используя таблицы истинности.
Теорема. Для произвольной формулы существует равносильная ей формула, которая содержит только знаки отрицания и дизъюнкции.
Действительно, в произвольной формуле %%X%% могут присутствовать знаки конъюнкции, импликации и эквиваленции. Избавимся от этих знаков, заменяя подформулы, содержащие эти знаки, на равносильные им по следующим правилам:
Но использование только двух знаков очень неудобно, так как приводит к очень громоздким формулам, именно поэтому, обычно, используют три основных знака: отрицание, конъюнкция и дизъюнкция.
Обратная и противоположная теоремы
Назовем теорему %%T = A \rightarrow B%% прямой теоремой. Составим следующие высказывания:
Между этими теоремами есть следующие связи:
Доказать что формулы логически эквивалентны
Равносильные формулы алгебры логики
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр., 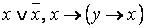
Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр., 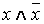
Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.
Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A ↔ B тавтология, и обратно, если формула A ↔ B тавтология, то формулы A и B равносильны.
Равносильности алгебры логики можно разбить на 3 группы:
1. Основные равносильности.
· 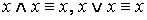
· 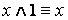
· 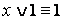
· 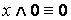
· 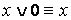
· 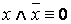
· 
· 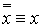
· 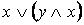
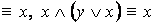
1. Равносильности, выражающие одни логические операции через другие:
· 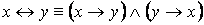
· 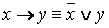
· 
· 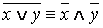
· 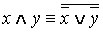
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как 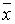
Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:
1) Связка Шеффера – дизъюнкция отрицаний.
Обозначение. x | y ≡ 
Логические значения связки Шеффера описываются следующей таблицей истинности:
2) Связка Лукасевича – конъюнкция отрицаний.
Логические значения связки Лукасевича описываются следующей таблицей истинности:
2. Равносильности, выражающие основные законы алгебры логики:
· 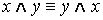
· 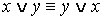
· 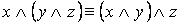
· 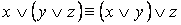
· 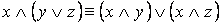
· 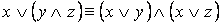
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.
Равносильные преобразования формул
Используя равносильности групп 1–3 можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.