Доказать что множество замкнуто
Замкнутые и открытые множества
Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.
Приведем примеры замкнутых и открытых множеств. Всякий отрезок есть замкнутое множество, а всякий интервал — открытое множество. Несобственные полуинтервалы и замкнуты, а несобственные интервалы и открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек
Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.
1. Пересечение любого числа замкнутых множеств замкнуто.
2. Сумма любого числа открытых множеств есть открытое множество.
3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.
4. Если множество замкнуто, то его дополнение открыто и обратно.
Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.
В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).
Как видно из нижеследующего примера, замкнутые множества могут иметь весьма сложное строение.
Канторово совершенное множество
Рассмотрим некоторые свойства этого множества. Множество замкнуто, так как оно образуется путем удаления из прямой некоторого, множества непересекающихся интервалов. Множество не пусто; во всяком случае в нем содержатся концы всех выброшенных интервалов.
Можно показать, что множество имеет мощность континуума. В частности, отсюда следует, что канторово совершенное множество содержит, кроме концов смежных интервалов, еще и другие точки. Действительно, концы смежных интервалов образуют лишь счетное множество.
Разнообразные типы точечных множеств постоянно встречаются в самых различных разделах математики, и знание их свойств совершенно необходимо при исследовании многих математических проблем. Особенно большое значение имеет теория точечных множеств для математического анализа и топологии.
Исследования Н.Н. Лузина и его учеников показали, что имеется глубокая связь между дескриптивной теорией множеств и математической логикой. Трудности, возникающие при рассмотрении ряда задач дескриптивной теории множеств (в частности, задач об определении мощности тех или иных множеств), являются трудностями логической природы. Напротив, методы математической логики позволяют более глубоко проникнуть в некоторые вопросы дескриптивной теории множеств.
Математика, физика на «отлично»
Открытые и замкнутые множества
В курсе математического анализа на первом курсе ВУЗов встречается много непонятного и непривычного. Одна из первых таких «новых» тем — это открытые и замкнутые множества. Постараемся дать пояснения по данной тематике.
Перед тем, как приступить к постановке определений и задач, напомним значение используемых обозначений и кванторов :
∈ — принадлежит
∅ — пустое множество
Ε — множество действительных чисел
х* — закреплённая точка
А* — множество граничных точек
: — такое, что
⇒ — следовательно
∀ — для каждого
∃ — существует
Uε(х) — окрестность х по ε
Uºε(х) — проколотая окрестность х по ε
Итак,
Определение 1: Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М
С помощью кванторов определение запишется следующим образом:
М ∈ Ε — открытое, если ∀ у∈М ∃ ε>0 : Uε(y) Определение 2: Точка x* ∈ E называется граничной точкой множества М, если в любой окрестности точки х содержатся точки как из множества М, так и из его дополнения.
Теперь с помощью кванторов:
х*∈ E — граничная точка, если ∀Uε(x) ∩ М ≠ ∅ и ∀Uε(x) ∩ Е\М
Определение 3: Множество называется замкнутым, если ему принадлежат все граничные точки. Пример — отрезок [a, b]
Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).
Докажем несколько теорем, связанных с открытым и замкнутым множествами.
Теорема 1: Пусть множество А — открытое. Тогда дополнение к множеству А является замкнутым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — незамкнутое. Тогда существует граничная точка х*, которая не принадлежит В, а значит — принадлежит А. По определению граничной точки окрестность х* имеет пересечение как с В, так и с А. Однако с другой стороны х* является внутренней точкой открытого множества А, поэтому вся окрестность точки х* лежит в А. Отсюда делаем вывод, что множества А и В пересекаются не по пустому множеству. Такого быть не может, поэтому наше предположение неверно и В является замкнутым множеством, ч. т. д.
В кванторах доказательство можно записать короче:
Предположим, что В — незамкнутое, тогда:
(1) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ∩ В ≠ ∅ (определение граничной точки)
(2) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ⊂ А ≠ ∅ (определение открытоко множества)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — замкнутое, ч. т. д.
Теорема 2: Пусть множество А — замкнутое. Тогда дополнение к множеству А является открытым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — замкнутое множество. Тогда любая граничная точка лежит в В. Но так как А — также замкнутое множество, то все граничные точки принадлежат и ему. Однако точка не может одновременно принадлежать множеству и его дополнению. Противоречие. В — открытое множество, ч. т. д.
В кванторах это выглядеть будет следующим образом:
Предположим, что В — замкнутое, тогда:
(1) ∀ х∈А*:х∈A (из условия)
(1) ∀ х∈А*:х∈В (из предположения)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — открытое, ч. т. д.
Теорема 3: Пусть множество А — замкнутое и открытое. Тогда А = Е или А = ∅
Доказательство: Начнём записывать подробно, но сразу использую кванторы.
Предположим, что множество С — замкнутое и открытое, причём С ≠ ∅ и С ≠ Е. Тогда очевидно, что С ⊆ Е.
(1) ∃ х∈А*:х∈С ⇒ ∀Uε(x) ∩ Е\С ≠ ∅ (определение граничной точки, которая принадлежит С)
(2) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ⊂ В (определение открытого множества С)
Из (1) и (2) следует, что Е\С ∩ С ≠ ∅, но это неверно. Противоречие. С не может быть одновременно и открытым, и замкнутым, ч. т. д.
Математический анализ — это фундаментальная математика, сложная и непривычная для нас. Но надеюсь, что-то стало понятнее после прочтения статьи. В добрый путь!
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Замкнутость множества граничных точек
Задание: показать, что множество граничных точек любого множества Е (Е подмножество 
Доказательство:От противного. Предположим, что существут предельная точка Х(т.е.множество предельных точек незамкнуто), не принадлежащая множеству граничных точек. В ее окрестности сожержица хотя бы одна граничная точка, => в ее окрестности сожержатся как точки принадлежещие множеству граничных точек, так и нет => по опрелению граничной точки Х тоже будет граничной точкой и будет принадлежать множеству граничных точек => противоречие и множество замкнуто.
Если што неправильно, плз исправьте.
При перемещении в тематический раздел заголовок изменен на более информативный. Первоначальный: «Проверьте плз доказательство». / GAA
| Заслуженный участник |
| Заслуженный участник |
Вообще-то смотря что изначально называть граничными точками. Мне кажется, наиболее разумно определять границу как разность между замыканием и внутренностью области. Тогда замкнутость границы почти тривиальна.
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Доказательство для произвольного топологического пространства 

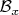


Пусть 




















| Заморожен |
А начерта Вам база топологии? Почему бы с самим фильтром окрестностей не работать? То есть оставить то же самое, но называть «окрестностями» не элементы базы фильтра, а сами элементы фильтра окрестностей.
Добавлено спустя 2 минуты 58 секунд:
Упс, пардон, понял. Вам нужны открытые окрестности. То есть наличие в каждой точке базы фильтра окрестностей, состоящей из открытых множеств.
Кстати, я вот уже точно не помню, чем топология отличается от предтопологии. Случайно не этим самым (наличием у каждой точки базы фильтра окрестностей, состоящей из открытых множеств)?
| Заслуженный участник |
В топологии обычно окрестностью точки или множества называют любое открытое множество, содержащее данную точку или множество. Если я буду употреблять термин «окрестность» в таком смысле, то доказательство замкнутости границы сильно упростится и будет меньше похоже на то, что излагали предшественники. Для придания некоторого сходства я и ввёл эти базы.
Что касается использования окрестностей, не являющихся открытыми множествами, то оно вполне возможно, но, как правило, не практикуется, так как обычно усложняет рассуждения.
Этим самым (С.С.Кутателадзе. Основы функционального анализа. Глава 9).

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Замкнутость множеств
Определение: Множество A называется замкнутым относительно операции *, если результат применения этой операции к любым элементам множества A также является элементом множества A. (Если для любых a,bÎ A, a*bÎ A, то множество A замкнуто относительно операции *)
Для доказательства замкнутости множества относительно операции необходимо либо непосредственным перебором всех случаев убедиться в этом (пример 1б), либо провести рассуждение в общем виде (пример 2). Чтобы опровергнуть замкнутость, достаточно привести один пример, демонстрирующий нарушение замкнутости (пример 1а).
а) В качестве операции * возьмем арифметическую операцию сложения (+). Исследуем множество A на замкнутость относительно операции сложения (+):
0 + 1 = 1 Î A; 0 + 0 = 0 Î A; 1 + 0 = 1Î A; 1 + 1 = 2 Ï A.
Имеем, что в одном случае (1+1) результат применения операции (+) к элементам множества A не принадлежит множеству A. На основании этого делаем вывод о том, что множество A не является замкнутым относительно операции сложения.
б) Теперь в качестве операции * возьмем операцию умножения (×).
0×1 = 0 Î A; 0×0 = 0 Î A; 1×0 = 0 Î A; 1×1 = 1 Î A.
Для любых элементов множества A результат применения операции умножения также является элементом множества A. Следовательно, A замкнуто относительно операции умножения.
Исследовать на замкнутость относительно четырех арифметических операций множество целых чисел, кратных 7.
Z7 = <7n, n Î Z> – множество чисел, кратных семи.
Очевидно, что Z7 – незамкнуто относительно операции деления, так как, например,
Докажем замкнутость множества Z7 относительно операции сложения. Пусть m, k – произвольные целые числа, тогда 7mÎ Z7 и 7kÎ Z7. Рассмотрим сумму 7m + 7 k = 7∙(m + k).
Имеем mÎ Z, kÎ Z. Z – замкнуто относительно сложения Þ m + k = l – целое число, то есть l Î Z Þ 7l Î Z7.
Таким образом, для произвольных целых чисел m и k доказали, что (7m + 7 k) Î Z7. Следовательно, множество Z7 замкнуто относительно сложения. Аналогично доказывается замкнутость относительно операций вычитания и умножения (проделайте это самостоятельно).