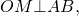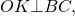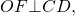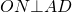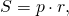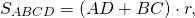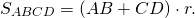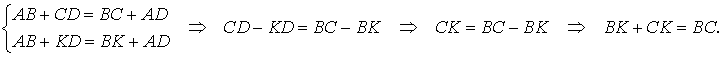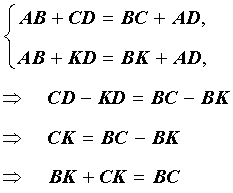Доказать что в четырехугольник можно вписать окружность
Четырехугольники, вписанные в окружность. Теорема Птолемея
Вписанные четырёхугольники и их свойства
Теорема 1 доказана.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
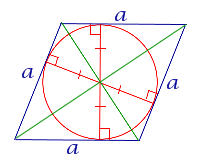
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | |||||||||||||||||||||||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||||||||||||||||||
| Окружность, описанная около ромба | |||||||||||||||||||||||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||||||||||||||||||
| Окружность, описанная около трапеции | |||||||||||||||||||||||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||||||||||||||||||
| Окружность, описанная около дельтоида | |||||||||||||||||||||||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||||||||||||||||||
| Произвольный вписанный четырёхугольник | |||||||||||||||||||||||
 | |||||||||||||||||||||||
| Окружность, описанная около ромба | |||||||||||||||||||||||
 Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |||||||||||||||||||||||
| Окружность, описанная около трапеции | |||||||||||||||||||||||
 Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |||||||||||||||||||||||
| Окружность, описанная около дельтоида | |||||||||||||||||||||||
 Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |||||||||||||||||||||||
| Произвольный вписанный четырёхугольник | |||||||||||||||||||||||
 Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, Теорема ПтолемеяДокажем, что справедливо равенство: Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4). откуда вытекает равенство:
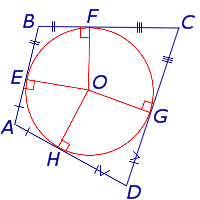
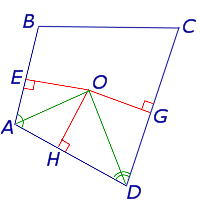
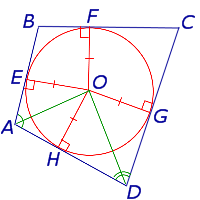
Вписанная в четырехугольник окружностьОписанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник. Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности? В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.
И обратно, если суммы противоположных сторон четырехугольника равны: то в четырехугольник ABCD можно вписать окружность. Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.
AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD, то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д. 3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.
5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой где p — полупериметр четырехугольника. Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон. Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и Соответственно, радиус вписанной в четырехугольник окружности равен Вписанный четырехугольник и его свойства (ЕГЭ 2022)Мы видели, что вокруг всякого треугольника можно описать окружность. Вот так: Вопрос: а можно ли получить вписанный четырехугольник? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника? Сейчас мы это выясним! Вписанный четырехугольник — коротко о главном
\( \displaystyle \angle B+\angle D=180<>^\circ \).
Вписанный четырехугольник — определения и теоремыВот оказывается, что это неправда! НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:
На нашем рисунке: \( \displaystyle \alpha +\beta =180<>^\circ \) Посмотри, углы \( \displaystyle \alpha \) и \( \displaystyle \beta \) лежат друг напротив друга, значит, они противоположные. А что же тогда с углами \( \displaystyle \varphi \) и \( \displaystyle \psi \)? Они вроде бы тоже противоположные? Можно ли вместо углов \( \displaystyle \alpha \) и \( \displaystyle \beta \) взять углы \( \displaystyle \varphi \) и \( \displaystyle \psi \)? Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет \( \displaystyle 180<>^\circ \). Оставшиеся два угла тогда сами собой тоже дадут в сумме \( \displaystyle 180<>^\circ \). Не веришь? Давай убедимся. Пусть \( \displaystyle \alpha +\beta =180<>^\circ \). Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, \( \displaystyle 360<>^\circ \). То есть \( \displaystyle \alpha +\beta +\varphi +\psi =360<>^\circ \) — всегда! \( \displaystyle 180<>^\circ \) Так что запомни крепко-накрепко:
Доказательство смотри чуть дальше. А пока давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна \( \displaystyle 180<>^\circ \). Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма? Вписанный параллелограммПопробуем сперва «методом научного тыка»: Вот как-то не получается. Теперь применим знание: Предположим, что нам как-то удалось посадить на параллелограмм \( \displaystyle ABCD\) окружность. Тогда непременно должно быть: \( \displaystyle \alpha +\beta =180<>^\circ \), то есть \( \displaystyle \angle B+\angle D=180<>^\circ \). А теперь вспомним о свойствах параллелограмма: у всякого параллелограмма противоположные углы равны. То есть \( \displaystyle \angle B = \angle D\). У нас получилось, что \( \displaystyle \left\< \begin А что же углы \( \displaystyle A\) и \( \displaystyle C\)? Ну, то же самое конечно. \( \displaystyle ABCD\) – вписанный → \( \displaystyle \angle A+\angle C=180<>^\circ \) → \( \displaystyle \angle A=90<>^\circ \) \( \displaystyle ABCD\) — параллелограмм→ \( \displaystyle \angle A=\angle C\) → \( \displaystyle \angle C=90<>^\circ \) Описанные четырехугольникиAH = AE, BF = BE, CF = CG, DH = DG, Складывая эти равенства, получим: AH + BF + CF + DH = то справедливо равенство что и требовалось доказать. Следовательно, справедливы равенства Окружность касается касается стороны BC (рис.4). В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана. Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства: Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен. Итак, возможен и реализуется лишь случай 1. Из доказательства теоремы 2 непосредственно вытекает В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений. Примеры описанных четырёхугольников
| |||||||||||||||||||||||
| Квадрат | |||||||||||||||||||||||
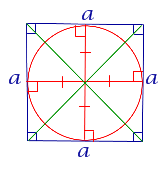 В любой квадрат можно вписать окружность | |||||||||||||||||||||||
| Прямоугольник | |||||||||||||||||||||||
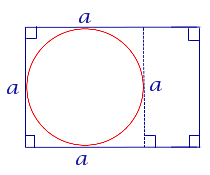 В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом | |||||||||||||||||||||||
| Параллелограмм | |||||||||||||||||||||||
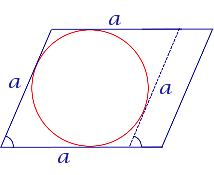 В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом | |||||||||||||||||||||||
| Дельтоид | |||||||||||||||||||||||
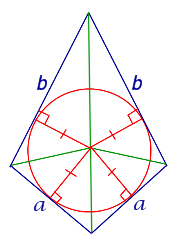 | |||||||||||||||||||||||
| Трапеция | |||||||||||||||||||||||
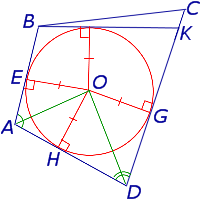
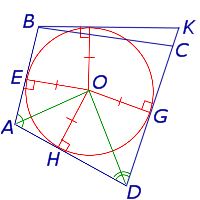
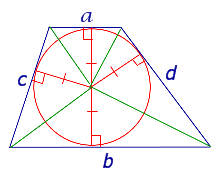 В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равныПусть окружность вписана в четырехугольник АВСD. Докажем, что суммы длин противоположных сторон четырехугольника равны. Отрезки касательных, проведенных к окружности из точек А, В, С и D, обозначим соответственно а, b, с и d. Докажем обратное утверждение. Пусть в четырехугольнике АВСD равны суммы длин противоположных сторон: АВ + СD = АD + ВС. Докажем, что в четырехугольник АВСD можно вписать окружность. Проведем AO и BO – биссектрисы углов A и B, AO ∩ BO = O. Точка O равноудалена от сторон AB, BC и AD четырёхугольника АВСD. Окружность с центром О касается сторон АВ, ВС и AD четырехугольника. Предположим, что это не так, и CD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай. Проведем касательную параллельно CD. Четырехугольник – описанный вокруг окружности, и для него выполняется равенство: Получили, что для четырехугольника длина стороны CD равна сумме трех других сторон. Это невозможно. Мы пришли к противоречию. Предположение о том, что CD не имеет общих точек с окружностью, было неверно. Аналогично доказывается, что CD не может быть секущей к окружности. Значит, CD – касательная к окружности и четырехугольник ABCD – описанный вокруг окружности. Задача ЕГЭ по теме «Описанный четырехугольник» В четырёхугольник ABCD вписана окружность, AB=10, CD=16. Найдите периметр четырёхугольника ABCD. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,
| |||||||||||||||||||||||










 В четырехугольник ABCD можно вписать окружность, если
В четырехугольник ABCD можно вписать окружность, если O — точка пересечения биссектрис четырехугольника ABCD.
O — точка пересечения биссектрис четырехугольника ABCD. AM=AN,
AM=AN,