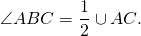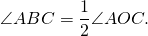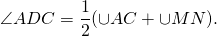Докажите что угол вершина которого лежит вне окружности а стороны пересекают окружность

09.09.202311.09.2023 admin 0 Comments

Углы в окружности

Рассмотрим углы в окружности и углы, связанные с окружностью.

I. Угол с вершиной в центре окружности называется центральным углом.

Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.

Например, центральному углу AOC соответствует дуга AC (или дуга AFC. Обычно дугу называют двумя буквами. Но, поскольку любую из двух, на которые точки A и C делят окружность, можно назвать AC, то третью, дополнительную букву, иногда используют для уточнения выбранной дуги).

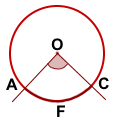
Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:

II. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

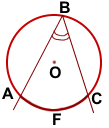
Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.

Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).

Вписанный угол равен половине дуги, на которую он опирается:

Есть другой вариант формулировки свойства вписанного угла.

Вписанный угол равен половине соответствующего ему центрального угла:

Вписанный угол, опирающийся на полуокружность — прямой.

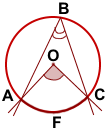
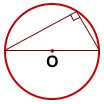
И наоборот: любой прямой вписанный угол опирается на полуокружность.

Другая формулировка этого утверждения:

(обратно: Если вписанный угол прямой, то он опирается на диаметр).

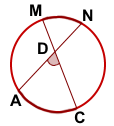
III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.

Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.

IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.

Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.

Источник

Контрольные вопросы 1. Что такое преобразование подобия? 2. Что такое гомотетия (центр гомотетии, коэффициент гомотетии)? 3. Докажите, что гомотетия есть преобразование подобия. 4. Какие свойства преобразования подобия вы знаете? Докажите, что преобразование подобия сохраняет углы между полупрямыми. 5. Какие фигуры называются подобными? 6. Каким знаком обозначается подобие фигур? Как записывается подобие треугольников? 7. Сформулируйте и докажите признак подобия треугольников по двум углам. 8. Сформулируйте и докажите признак подобия треугольников по двум сторонам и углу между ними. 9. Сформулируйте и докажите признак подобия треугольников по трём сторонам. 10. Докажите, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. 11. Докажите, что высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу. 12. Докажите, что биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. 13. Что такое плоский угол? 14. Что такое центральный угол? 15. Какой угол называется вписанным в окружность? 16. Докажите, что вписанный в окружность угол равен половине соответствующего центрального угла. 17. Докажите, что угол, вершина которого лежит внутри окружности, равен полусумме двух центральных углов, которым соответствуют дуги окружности, заключённые между сторонами данного угла и их продолжениями. 18. Докажите, что угол, вершина которого лежит вне окружности, а стороны пересекают окружность, равен полуразности двух центральных углов, которым соответствуют дуги окружности, заключённые между сторонами данного угла. 19. Сформулируйте и докажите теорему об угле между хордой и касательной к окружности. 20. Докажите свойства отрезков пересекающихся хорд и свойства отрезков секущих. 21. Какие свойства геометрических фигур иллюстрируют фотографии (с. 154—162)? Приведите свои примеры, иллюстрирующие эти свойства.

Источник

Углы, связанные с окружностью

Вписанные и центральные углы

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема
Вписанный угол

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности