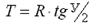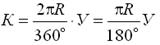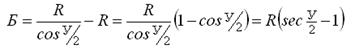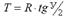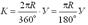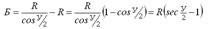какие точки круговой кривой называются главными

Основные элементы кривой и как они определяются. Разбивка закруглений в углах поворота и нахождение главных точек кривой

Разбить кривую в главных точках на местности – значит найти положение её главных точек на оси линейного сооружения и закрепить их. Положение начала кривой НКК определяют, отложив вычисленное расстояние от ближайшего пикета.

В нашем примере (рис. 84) ближайшим пикетом является ПК1. От него к ПК0 откладывают расстояние 27,67. В этой точке забивают колышек, а на расстоянии 15 – 20 см по направлению трассы забивают сторожок и на нем записывают НКК ПК0 + 72.33.

Середину кривой СКК закрепляют, отложив от ВУ по направлению биссектрисы угла, образованного направлениями трассы, отрезок, равный Б.

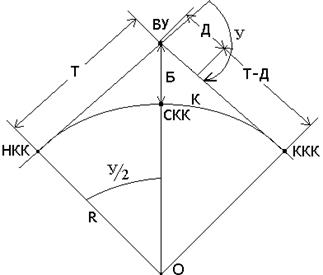
Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами (рис. 83).

Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; середина круговой кривой СКК; конец круговой кривой ККК.

Рис. 83. Схема круговой кривой.

Основными элементами кривой являются:

1. Угол поворота трассы У.

2. Радиус закругления R.

Во время изысканий угол У вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НКК, О (рис. 83).

3. Тангенс кривой (касательная) Т – расстояние по прямой от вершины угла до начала или конца кривой.

4. Длина кривой К от начала кривой до её конца.

5. Биссектриса кривой Б – отрезок от вершины угла до середины кривой.

Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы для разбивки кривых.

Источник

Круговые и переходные кривые.

Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).

Рис. 15.3 Схема круговой кривой

Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:

Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):

Домер вычисляют по формуле

. (15.2)

Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.

В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:

Правильность вычислений контролируют по формулам:

Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.

По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.

Вычислим пикетажное положение главных точек:

ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00

ПК НК 5 + 39,27 7 + 32,73

ПК КК 7 + 31,08 ПК КК 7 + 31,08

ПК НК 5 + 39,27 ПК ВУ 6 + 36,00

ПК СК 6 + 35,17 ПК СК 6 + 35,18

Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим

,

R – радиус кривизны в конце переходной кривой.

Индексом k отмечены значения переменных в конце переходной кривой.

Для радиуса кривизны переходной кривой в текущей точке i найдём:

где через l обозначена длина переходной кривой s_k. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.

Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол

.

Подставляя выражение радиуса кривизны r из (15.5), получим

.

Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:

,

Рис. 15.4 Схема переходной кривой:

а – углы поворота трассы: φ – в текущей точке i, β – в конце

Из полученного уравнения вытекают формулы:

; ; l = 2Rb, (15.6)

Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):

Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):

Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:

; (15.8)

. (15.9)

Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:

,

Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.

Рис. 15. 5 Смещение начала переходной кривой

Рис. 15.6 Сопряжение круговой кривой

Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q₁ и имеющая длину K = Ra.

При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна

Тангенс и биссектриса определяются по формулам:

Домер в этом случае равен

.

В полевых условиях значения m, Т_p и Б_p вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).

Источник

Разбивка главных точек круговых кривых

В плане ось трассы представляет собой сочетание прямых и кривых участков. В каждой вершине поворота трассы две смежные линии ее сопрягаются кривой. Кривые могут иметь форму круговой или суммарной кривой. Суммарная кривая состоит из двух переходных кривых и круговой кривой.

Рассмотрим круговую кривую (рисунок 6.6). Круговая кривая – это дуга окружности, вписанная в угол, образованный двумя смежными линиями трассы. Круговая кривая имеет три главные точки и шесть элементов.

Г л а в н ы м и т о ч к а м и круговой кривой являются начало круговой кривой (НКК), конец круговой кривой (ККК) и середина круговой кривой (СКК).

На плане и на местности эти точки могут быть получены, если известны следующие элементы кривой:

1 – угол поворота трассы (φ);

2 – радиус круговой кривой (R);

3 – расстояние от вершины угла поворота (ВУП) до начала или конца кривой, которое называется тангенс (Т);

4 – длина кривой, расстояние от ее начала до ее конца (К);

5 – расстояние от вершины угла поворота до середины кривой, которое называется биссектриса кривой (Б);

6 – домер, показывающий, на сколько путь от начала до конца кривой

по касательной больше, чем по кривой (Д).

Угол поворота трассы (φ) измеряют при трассировании, а величину радиуса кривой (R) выбирают в соответствии с техническими условиями.

Остальные элементы круговой кривой могут быть определены из прямоугольного треугольника (О – НКК – ВУП) на рисунке 6.6 по следующим формулам:

По вышеприведенным формулам составлены таблицы, в которых по известным φ и R находят элементы Т, К, Б и Д (например, Власов Д.И., Логинов В.Н. Таблицы для разбивки кривых на железных дорогах [3].

Так, например для φ = 24 0 30′; R = 400 м; Т = 86,85 м; К = 171,04 м; Б = = 9,32 м; Д = 2,65 м.

На местности начало и конец кривой получают, откладывая величины тангенса от вершины угла поворота (ВУП) по линиям трассы, а середину кривой (СКК) – отложением величины Б по биссектрисе угла (β/2):

Этот угол откладывают при помощи теодолита. Точка О на местности не определяется и не обозначается (рисунок 6.6). Для облегчения разбивки длинных кривых их целесообразно разделить на несколько равных частей, называемых кратными кривыми.

Чтобы определить элементы круговых кривых для больших углов поворота при любой величине радиуса, например R = 600 м, можно определить из таблицы 1 [3] элементы для радиуса R = 100 м и найденные значения умножить на отношение радиусов 600:100 = 6, так как величины Т, К, Б, Д пропорциональны радиусу кривой. Это видно из формул (1.3).

Дата добавления: 2015-01-19 ; просмотров: 2248 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Основные элементы круговой кривой. Расчет

На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.

На железнодорожных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами СТН Ц-01-95.

Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами (рис. 83).

Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; середина круговой кривой СКК; конец круговой кривой ККК.

Основными элементами кривой являются:

1. Угол поворота трассы У.

2. Радиус закругления R.

Во время изысканий угол У вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НКК, О (рис. 83).

3. Тангенс кривой (касательная) Т – расстояние по прямой от вершины угла до начала или конца кривой.

4. Длина кривой К от начала кривой до её конца.

5. Биссектриса кривой Б – отрезок от вершины угла до середины кривой.

6. Домер Д – разность между длиной двух тангенсов и кривой.

Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы для разбивки кривых.

Вычислить пикетажные значения главных точек кривой – значит узнать на каких пикетах и плюсовых точках они находятся.

Сначала определяют пикетаж вершины угла поворота ВУ, а затем находят пикетажное значение начала, конца и середины кривой

.

Источник

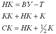
6.5 Круговые кривые, их элементы и главные точки.

Разбивка главных точек круговых кривых

В плане ось трассы представляет собой сочетание прямых и кривых участков. В каждой вершине поворота трассы две смежные линии ее сопрягаются кривой. Кривые могут иметь форму круговой или суммарной кривой. Суммарная кривая состоит из двух переходных кривых и круговой кривой.

Рассмотрим круговую кривую (рисунок 6.6).Круговая кривая – это дуга окружности, вписанная в угол, образованный двумя смежными линиями трассы. Круговая кривая имеет три главные точки и шесть элементов.

Г л а в н ы м и т о ч к а м и круговой кривой являются начало круговой кривой (НКК), конец круговой кривой (ККК) и середина круговой кривой (СКК).

На плане и на местности эти точки могут быть получены, если известны следующие элементы кривой:

1 – угол поворота трассы (φ);

2 – радиус круговой кривой (R);

3 – расстояние от вершины угла поворота (ВУП) до начала или конца кривой, которое называется тангенс (Т);

4 – длина кривой, расстояние от ее начала до ее конца (К);

5 – расстояние от вершины угла поворота до середины кривой, которое называется биссектриса кривой (Б);

6 – домер, показывающий, на сколько путь от начала до конца кривой

по касательной больше, чем по кривой (Д).

Угол поворота трассы (φ) измеряют при трассировании, а величину радиуса кривой (R) выбирают в соответствии с техническими условиями.

Остальные элементы круговой кривой могут быть определены из прямоугольного треугольника (О – НКК – ВУП) на рисунке 6.6 по следующим формулам:

По вышеприведенным формулам составлены таблицы, в которых по известным φ и R находят элементы Т, К, Б и Д (например, Власов Д.И., Логинов В.Н. Таблицы для разбивки кривых на железных дорогах [3].

Так, например для φ = 24 0 30′; R = 400 м; Т = 86,85 м; К = 171,04 м; Б = = 9,32 м; Д = 2,65 м.

На местности начало и конец кривой получают, откладывая величины тангенса от вершины угла поворота (ВУП) по линиям трассы, а середину кривой (СКК) – отложением величины Б по биссектрисе угла (β/2):

Этот угол откладывают при помощи теодолита. Точка О на местности не определяется и не обозначается (рисунок 6.6). Для облегчения разбивки длинных кривых их целесообразно разделить на несколько равных частей, называемых кратными кривыми.

Чтобы определить элементы круговых кривых для больших углов поворота при любой величине радиуса, например R = 600 м, можно определить из таблицы 1 [3] элементы для радиуса R = 100 м и найденные значения умножить на отношение радиусов 600:100 = 6, так как величины Т, К, Б, Д пропорциональны радиусу кривой. Это видно из формул (1.3).

Источник