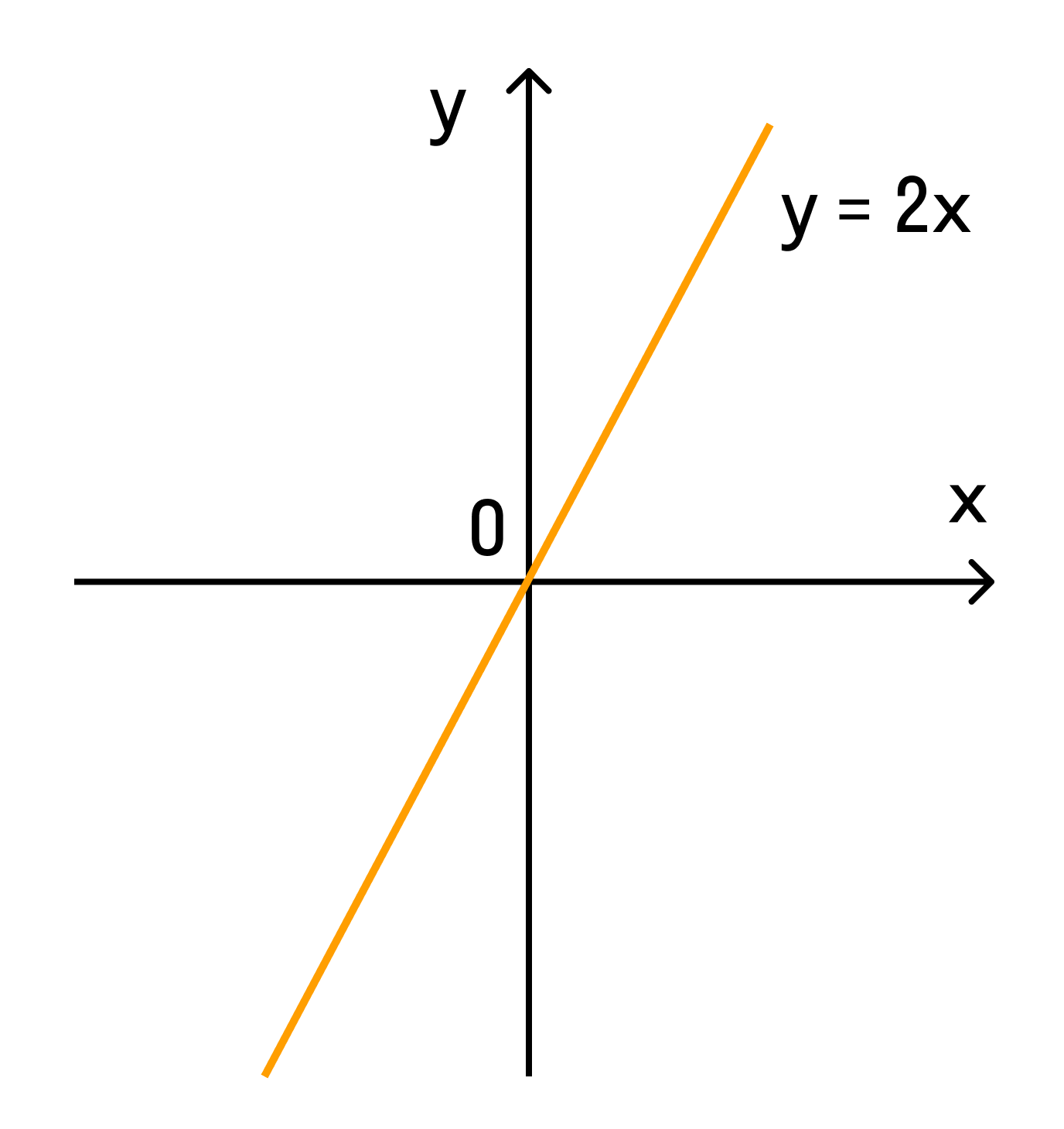Распределяется пропорционально это как
Пропорциональное распределение доли общества при выходе участника из ООО
Инструкция по пропорциональному распределению доли
Распределение доли после выхода участника Общества
Законом установлено, что в течение одного года со дня перехода доли или части доли в Уставном капитале к Обществу они должны быть по решению общего собрания участников Общества распределены между всеми участниками Общества пропорционально их долям в Уставном капитале Общества или предложены для приобретения всем, либо некоторым участникам Общества.
В первом случае мы говорим о пропорционально распределении доли общества. Во втором случае имеется ввиду именно непропорциональное распределение. В этом случае между обществом в лице его руководителя и покупателем заключается договор купли-продажи.
Когда происходит пропорциональное распределение
В случае наличия у участников желания оставить прежним соотношения своих долей в уставном капитале, они принимают решение о пропорциональном распределении доли общества. Также необходимо, чтобы при расчете распределения доли была возможность математически верно рассчитать новое процентное соотношение долей.
Правильное пропорциональное распределение
Рассмотрим, как правильно распределить доли между участниками ООО при выходе одного или нескольких участников на примере:
В составе ООО три участника с нижеуказанными долями. Для удобства определим участникам ООО порядковые номера: 1, 2, 3. Размер уставного капитала – 10 000 рублей.
Из состава выходит участник №3. Задача: определить доли оставшихся участников после его выхода.
1 – 45% или 4 500 рублей или 45/100
2 – 30% или 3 000 рублей или 30/100
3 – 25% или 2 500 рублей или 25/100
Поскольку выходит участник №3 с долей 25% или 2 500 рублей, то нам необходимо распределить его долю среди оставшихся участников пропорционально их долям в уставном капитале ООО.
Для этого нам нужно, определить долю, принадлежащую ООО — 2 500 рублей или 25% или 25/100.
Определяем сумму долей, принадлежащих оставшимся участникам:
Доля участника №1 + доля участника №2 = 45% + 30% = 75%
В том числе доля участника №1 = 45/75
В том числе доля участника №2 = 30/75
Далее необходимо долю, принадлежащую ООО (2 500 рублей) умножить на вышеуказанные доли участников:
Участник №1 = 2 500 * 45/75 = 1 500 рублей
Участник №2 = 2 500 * 30/75 = 1 000 рублей
Т.е., из доли, принадлежащей ООО, участнику №1 переходит 1 500 рублей, а участнику №2 – 1 000 рублей.
Таким образом, после распределения доли ООО доли оставшихся участников увеличиваются не только в денежной выражении, но и в процентном:
Участник №1 = 4 500 + 1 500 = 6 000 рублей
Участник №2 = 3 000 + 1 000 = 4 000 рублей
Процентное выражение долей станет следующим (для этого необходимо денежное выражение доли участника поделить на общий размер уставного капитала и умножить на 100):
Участник №1 = 6 000 / 10 000 * 100 = 60%
Участник №2 = 4 000 / 10 000 * 100 = 40%
Также существует более простая формула для распределения доли принадлежащей Обществу между остальными участниками пропорционально.
Новая доля участника = сумма уставного капитала / (разделить на) суммарную долю в процентах остающихся участников х (умножить на) долю конкретного участника до распределения доли.
Таким образом будет вычислена новая доля участника в денежном выражении. Чтобы рассчитать в процентах нужно эту сумму разделить на сумму всего уставного капитала и умножить на 100.
Необходимые документы
Чтобы уведомить налоговую о факте пропорционального распределения доли одновременно с выходом участника потребуется следующий пакет документов:
Обратите внимание, что форма Р14001 с 25 ноября 2020 года больше не применяется. Новая форма Р13014 утверждена Приказом ФНС России от 31.08.2020 N ЕД-7-14/617@.
Пропорциональное деление
Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.
Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.
Деление числа на пропорциональные части
Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.
Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:
Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:
Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.
90 : (1 + 2 + 3) = 90 : 6 = 15;
Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.
Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.
Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:
значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то
Второй способ: обозначим искомые части буквами a, b и c:
Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:
Следовательно, c равно:
Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:
так как 15 + 10 + 8 = 33, то
Деление на части, обратно пропорциональные числам
Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как
Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:
Пропорциональное соотношение
Опубликовано 25.06.2021 · Обновлено 25.06.2021
Что такое Пропорциональное соотношение?
Понимание пропорциональности
Пропорциональное распределение поддерживает акционеров, гарантируя, что компания может придерживаться своей первоначальной цели и не отдавать предпочтение одним инвесторам по сравнению с другими (например, дает проценту акционеров желаемые денежные средства при передаче акций остальным). Хотя это означает, что каждый инвестор может не получить своего первоначального выбора; это гарантирует, что все инвесторы получат одинаковое вознаграждение.
Ключевые моменты
Пропорциональное распределение и дополнительные соображения по поводу слияния
Слияния происходят по нескольким причинам, в том числе для увеличения доли рынка за счет горизонтального слияния, снижения операционных издержек за счет вертикального слияния, выхода на новые рынки и / или объединения общих продуктов посредством родственного слияния – все для увеличения доходов и увеличения прибыли для выгода для акционеров фирмы. После слияния акции новой компании распределяются между существующими акционерами обоих первоначальных предприятий.
Примером слияния двух компаний в разных отраслях является слияние Amazon и Whole Foods в 2017 году, которое привлекло огромное внимание инвесторов и средств массовой информации. Amazon приобрела сеть магазинов органических продуктов Whole Foods за 13,7 млрд долларов наличными после одобрения акционеров и регулирующих органов. Для Amazon это стало крупным достижением в ее попытке продавать продукты в Интернете и ее конкуренции с розничным продавцом продуктов Walmart. Для Whole Foods это помогло решить некоторые финансовые трудности.
Принимая решение о слиянии, помимо того, как обе компании будут вознаграждать акционеров, важно принять во внимание рекомендации Федеральной торговой комиссии по поддержанию конкурентоспособности отрасли и недопущению создания монополий. Например, важно спросить, создаст ли предлагаемое слияние рыночное влияние или нет. Проблемы антимонопольного законодательства возникают, в частности, в связи с предполагаемым горизонтальным слиянием прямых конкурентов.
Пример пропорционального распределения
Предположим, компания решает приобрести другое предприятие за 100 миллионов долларов, которое состоит из 75% денежных средств и 25% капитала. Разделение денежных средств и капитала может быть пересмотрено, если большинство инвесторов приобретаемой компании решат получать оплату наличными. В этом случае компания-покупатель изменит свои бухгалтерские показатели, чтобы удовлетворить спрос на наличные деньги. Это приведет к тому, что каждый инвестор приобретенной компании получит меньше денежных средств, чем планировалось изначально. Halliburton пришлось пересмотреть свое первоначальное предложение о выкупе акций от 2013 года и уменьшить его на 67,9%, чтобы уравновесить спрос инвесторов и курс акций на тот момент.
Прямая и обратная пропорциональность
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
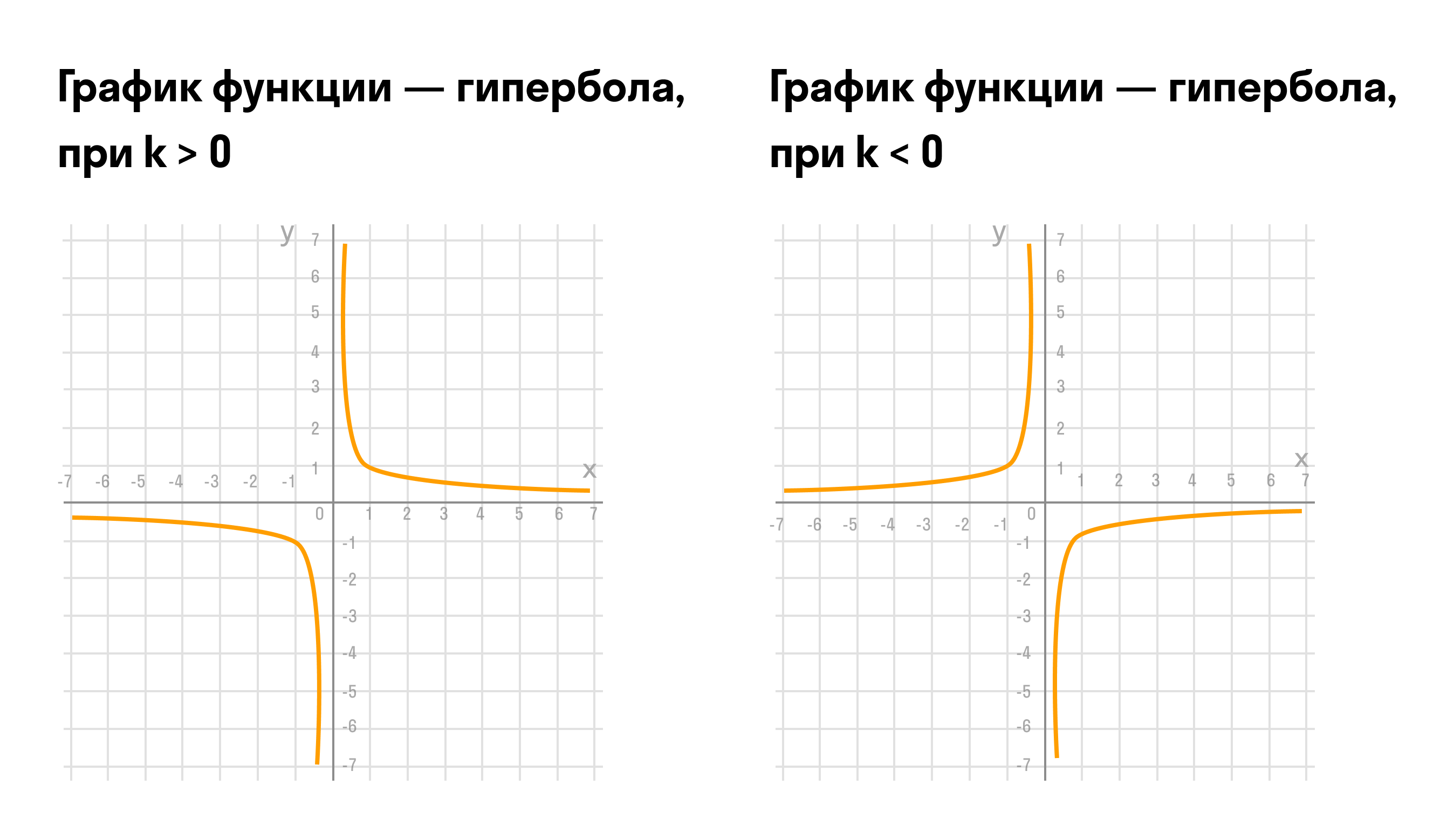
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
Пропорционально
Что такое Пропорционально?
Pro rata – это латинский термин, используемый для описания пропорционального распределения. По сути, это переводится как «пропорционально», что означает процесс, в котором все, что выделяется, будет распределяться равными частями.
Если что-то раздается людям на пропорциональной основе, это означает присвоение суммы одному человеку в соответствии с их долей в целом. Хотя пропорциональный расчет может использоваться для определения соответствующих частей любого данного целого, он часто используется в финансах бизнеса.
Ключевые моменты
Понимание Pro Rata
Пропорциональная ставка и дивиденды на акционера
Когда компания выплачивает дивиденды своим акционерам, каждому инвестору платят в соответствии с их долями. Например, если компания имеет 100 акций в обращении и выплачивает дивиденды в размере 2 долларов на акцию, общая сумма выплаченных дивидендов составит 200 долларов. Независимо от количества акционеров, общая сумма дивидендов не может превышать этот предел. В этом случае 200 долларов – это целое, и для определения соответствующей части этого целого, причитающейся каждому акционеру, необходимо использовать пропорциональный расчет.
Предположим, всего четыре акционера владеют 50, 25, 15 и 10 акциями соответственно. Сумма, причитающаяся каждому акционеру, является его пропорциональной долей. Он рассчитывается путем деления собственности каждого лица на общее количество акций и последующего умножения полученной доли на общую сумму выплаты дивидендов.
Следовательно, доля мажоритарного акционера составляет (50/100) x 200 долларов = 100 долларов. Это имеет смысл, потому что акционер владеет половиной акций и получает половину общих дивидендов. Остальные акционеры получают 50, 30 и 20 долларов соответственно.
Pro Rata для страховых взносов
Другое распространенное использование – определение суммы, причитающейся за частичный срок страхового полиса. Большинство страховых полисов рассчитаны на полный 12-месячный год, поэтому, если полис необходим на более короткий срок, страховая компания должна пропорционально распределить ежегодную премию, чтобы определить размер задолженности. Для этого разделите общую премию на количество дней в стандартном сроке и умножьте на количество дней, охватываемых усеченным полисом.
Например, предположим, что автомобильный полис, который обычно охватывает полный год, предусматривает премию в размере 1000 долларов США. Если застрахованному требуется полис только на 270 дней, компания должна соответственно уменьшить страховой взнос. Пропорциональная премия за этот период составляет (1000 долларов США / 365) x 270 = 739,73 доллара США.
Pro Rata для процентных ставок
Пропорциональные расчеты также используются для определения суммы процентов, которые будут получены от инвестиций. Если инвестиции приносят годовую процентную ставку, то пропорциональная сумма, полученная за более короткий период, рассчитывается путем деления общей суммы процентов на количество месяцев в году и умножения на количество месяцев в усеченном периоде. Сумма процентов, полученных за два месяца по инвестициям, приносящим 10% годовых, составляет (10% / 12) x 2 = 1,67%.
Что касается облигаций, выплата начисленных процентов рассчитывается пропорционально. Начисленные проценты – это общие проценты, накопленные по облигации с момента последней выплаты купона. Когда держатель облигации продает облигацию до даты следующего купона, он по-прежнему имеет право на проценты, начисляемые до момента продажи облигации. Покупатель облигации, а не эмитент, несет ответственность за выплату продавцу облигации начисленных процентов, которые прибавляются к рыночной цене.
Формула начисленных процентов выглядит следующим образом: