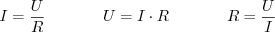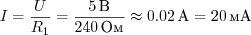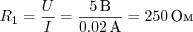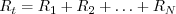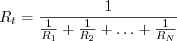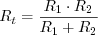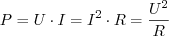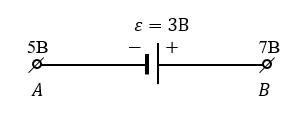Резисторы физика как решать
Резисторы: последовательное и параллельное соединение, токоограничивающие и подтягивающие сопротивления
Резистор (сопротивление) — один из наиболее распространённых компонентов в электронике. Его назначение — простое: сопротивляться течению тока, преобразовывая его часть в тепло.
Основной характеристикой резистора является сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем большая часть тока рассеивается в тепло. В схемах, питаемых небольшим напряжением (5 – 12 В), наиболее распространены резисторы номиналом от 100 Ом до 100 кОм.

Закон Ома
Закон Ома позволяет на заданном участке цепи определить одну из величин: силу тока I, напряжение U, сопротивление R, если известны две остальные:
Для обозначения напряжения наряду с символом U используется V.
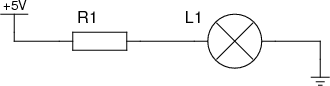
Рассмотрим простую цепь
Расчитаем силу тока, проходящего через резистор R1 и, соответственно, затем через лампу L1. Для простоты будем предполагать, что сама лампа обладает нулевым собственным сопротивлением.
Аналогично, если бы у нас был источник питания на 5 В и лампа, которая по документации должна работать при токе 20 мА, нам нужно бы было выбрать резистор подходящего номинала.
В данном случае, разница в 10 Ом между идеальным номиналом и имеющимся не играет большого значения: можно смело брать стандартный номинал — 240 или 220 Ом.
Аналогично, мы могли бы расчитать требуемое напряжение, если бы оно было не известно, а на руках были значения сопротивления и желаемая сила тока.
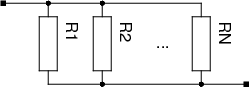
Соединение резисторов
При последовательном соединении резисторов, их сопротивление суммируется:
При параллельном соединении, итоговое сопротивление расчитывается по формуле:
Если резистора всего два, то:
В частном случае двух одинаковых резисторов, итоговое сопротивление при параллельном соединении равно половине сопротивления каждого из них.
Таким образом можно получать новые номиналы из имеющихся в наличии.
Применеие на практике
Среди ролей, которые может выполнять резистор в схеме можно выделить следующие:
Токоограничивающий резистор
Пример, на котором рассматривался Закон Ома представляет собой также пример токоограничевающего резистора: у нас есть компонент, который расчитан на работу при определённом токе — резистор снижает силу тока до нужного уровня.
В случае с Ардуино следует ограничивать ток, поступающий с выходных контактов (output pins). Напряжение, в состоянии, когда контакт включен (high) составляет 5 В. Исходя из документации, ток не должен превышать 40 мА. Таким образом, чтобы безопасно увести ток с контакта в землю понадобится резистор номиналом R = U / I = 5 В / 0.04 А = 125 Ом или более.
Стягивающие и подтягивающие резисторы
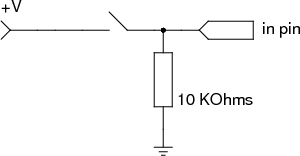
Стягивающие (pull-down) и подтягивающие (pull-up) резисторы используются в схемах рядом со входными контактами логических компонентов, которым важен только факт: подаётся ноль вольт (логический ноль) или не ноль (логическая единица). Примером являются цифровые входы Ардуино. Резисторы нужны, чтобы не оставить вход в «подвешенном» состоянии. Возьмём такую схему
Мы хотим, чтобы когда кнопка не нажата (цепь разомкнута), вход фиксировал отсутствие напряжения. Но в данном случае вход находится в «никаком» состоянии. Он может срабатывать и не срабатывать хаотично, непредсказуемым образом. Причина тому — шумы, образующиеся вокруг: провода действуют как маленькие антенны и производят электричество из электромагнитных волн среды. Чтобы гарантировать отсутствие напряжения при разомкнутой цепи, рядом с входом ставится стягивающий резистор:
Теперь нежелательный ток будет уходить через резистор в землю. Для стягивания используются резисторы больших сопротивлений (10 кОм и более). В моменты, когда цепь замкнута, большое сопротивление резистора не даёт большей части тока идти в землю: сигнал пойдёт к входному контакту. Если бы сопротивление резистора было мало (единицы Ом), при замкнутой цепи произошло бы короткое замыкание.
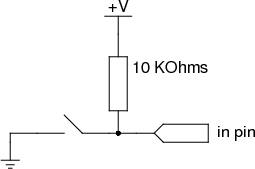
Аналогично, подтягивающий резистор удерживает вход в состоянии логической единицы, пока внешняя цепь разомкнута:
То же самое: используются резисторы больших номиналов (10 кОм и более), чтобы минимизировать потери энергии при замкнутой цепи и предотвратить короткое замыкание при разомкнутой.
Делитель напряжения
Делитель напряжения (voltage divider) используется для того, чтобы получить из исходного напряжения лишь его часть. Например, из 9 В получить 5. Он подробно описан в отдельной статье.
Мощность резисторов
Резисторы помимо сопротивления обладают ещё характеристикой мощности. Она определяет нагрузку, которую способен выдержать резистор. Среди обычных керамических резисторов наиболее распространены показатели 0.25 Вт, 0.5 Вт и 1 Вт. Для расчёта нагрузки, действующей на резистор, используйте формулу:
При превышении допустимой нагрузки, резистор будет греться и его срок службы может сильно сократиться. При сильном превышении — резистор может начать плавиться и вызвать воспламенение. Будьте осторожны!
Последовательное и параллельное соединение резисторов.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:
В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
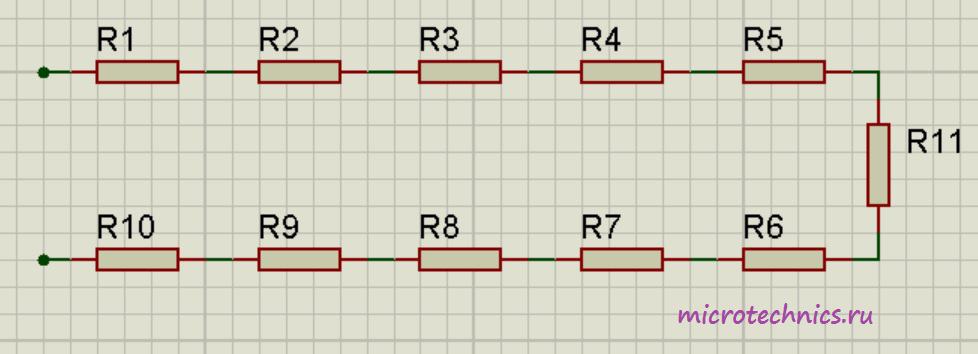
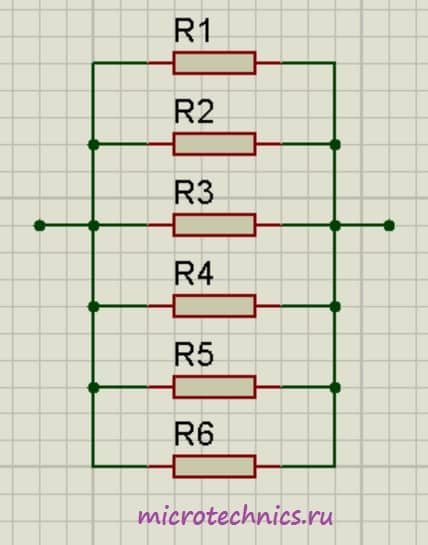
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
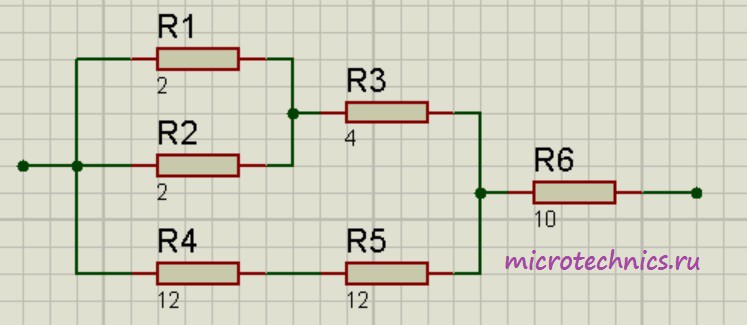
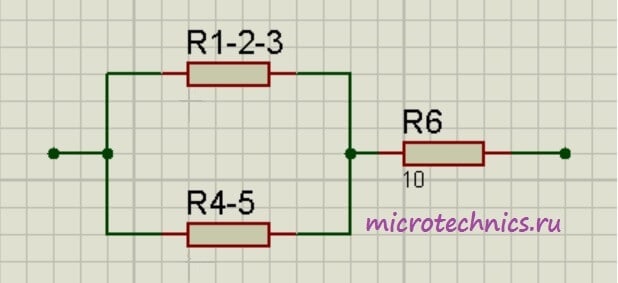
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 — они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_ <1-2>:
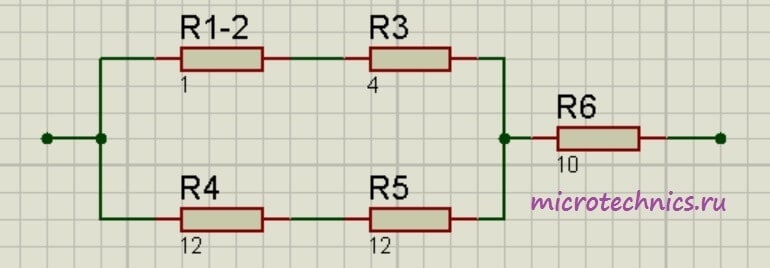
Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
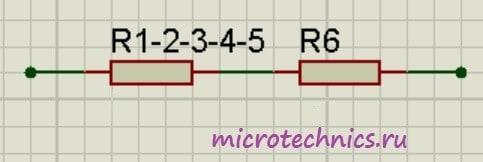
Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_ <1-2-3>и R_ <4-5>одним резистором R_ <1-2-3-4-5>:
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Задачи на закон Ома с решением
Знание закона Ома на сегодняшний день – вопрос общей эрудиции каждого человека. В сегодняшней статье займемся решением задач по теме «закон Ома».
Подписывайтесь на наш телеграм и получайте интересные новости каждый день! А если хотите получить скидку и не упустить выгоду – загляните на наш второй канал с приятными акциями и бонусами для клиентов.
Закон Ома: задачи с решением
Для новичков, которые только начинают решать задачи по физике, мы подготовили специальную памятку и собрали вместе более 40 формул по разным темам. Берите и пользуйтесь!
Задача на закон Ома №1
Условие
Определите силу тока в медном проводнике сеченим 0,5 мм2, если длина проводника 100 м, а напряжение на его концах равно 6,8 В.
Решение
Сначала запишем закон Ома:
В данном случае, чтобы найти силу тока I, нужно определить сопротивление R. Используем формулу с удельным сопротивлением и перепишем выражение для закона Ома:
R = ρ l S I = U S ρ l
Осталось подставить числа и рассчитать:
Ответ: 2 А.
Задача на закон Ома №2
Условие
По вольфрамовой проволоке длиной 3 м протекает электрический ток силой 0,04 А. Проволока находится под напряжением 5 В. Определите величину площади поперечного сечения проволоки.
Решение
Выразим площадь поперечного сечения проводника из формулы для сопротивления:
Сопротивление R найдем из закона Ома:
Подставим выражение для R в формулу для S и рассчитаем:
Задача на закон Ома №3
Условие
Каково напряжение на неоднородном участке цепи?
Решение
По закону Ома для неоднородного участка цепи:
Считая началом участка точку A, а концом – точку B, и беря поэтому ЭДС со знаком плюс (внутри источника направление тока от отрицательного полюса к положительному), получаем:
Ответ: 1В.
Нужно больше примеров решений задач? Вы найдете их в нашем блоге!
Задача на закон Ома №4
Условие
Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Решение
Это простейшая задача на закон Ома для участка цепи, которая решается в одно действие. Просто записываем закон Ома и производим расчет:
I = U R = 120 12 = 10 А
Ответ: 10 А.
Задача на закон Ома №5
Условие
Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.
Решение
Это задача на закон Ома для полной цепи. По закону Ома для замкнутой цепи:
Падение напряжения на внешнем участке цепи:
Падение напряжение на внутреннем участке цепи:
Ответ: 1,2 А; 10,8 В; 1,2 В.
Школьный учитель Георг Симон Ом открыл свой закон в 1826 году. Подробнее об истории открытия и самом законе Ома читайте в нашем блоге.
Вопросы на закон Ома
Вопрос 1. Сформулируйте закон Ома для однородного участка цепи.
Ответ. Закон Ома для однородного участка цепи нласит:
Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Вопрос 2. Сформулируйте закон Ома для замкнутой цепи.
Ответ. Закон Ома для замкнутой цепи гласит:
Величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Вопрос 3. От чего зависит сопротивление цепи?
Ответ. Сопротивление вещества обусловлено колебанием атомов кристаллической решетки.
Сопротивление зависит от:
Вопрос 4. Зависит ли сопротивление от напряжения и силы тока?
Ответ. Нет. Сопротивление не зависит от напряжения и силы тока в проводнике.
Вопрос 5. Всегда ли соблюдается закон Ома?
Ответ. Нет, не всегда. Например, закон Ома не действует при низких температурах для веществ, обладающих сверхпроводимостью.
Проблемы с учебой? Обращайтесь в профессиональный сервис для студентов за квалифицированной помощью.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Что такое резистор и для чего он нужен?
При передаче электрического тока на расстояние из-за сопротивления проводов теряется часть энергии. В таких случаях сопротивление является негативным фактором и его стараются свести к минимуму.
Другое дело электрические цепи в электронных устройствах. Там резистор выполняет много полезных функций. В электронных схемах используется свойства этих пассивных компонентов для ограничения тока в многочисленных цепях. С их помощью обеспечивается нужный режим работы усилительных каскадов.
Что такое резистор?
Название этого электронного элемента произошло от латинского слова resisto — сопротивляюсь. То есть – это пассивный элемент применяемый в электрических цепях, действие которого основано на сопротивлении току. Основной характеристикой этого электронного компонента является величина его электрического сопротивления.
Пассивность данного электронного компонента означает то, что основной его функцией является поглощение электрической энергии. В отличие от активных элементов электроники, он ничего не генерирует, а только пассивно рассеивает электричество, преобразуя его в тепло. В схемах замещения сопротивление является основным параметром, в то время как ёмкость и индуктивность – паразитные величины.
Применение
Резисторы применяются во всех электрических схемах для установления нужных значений тока в цепях, с целью демпфирования колебаний в различных фильтрах, в качестве делителей напряжений и т. п.
Резисторы выполняют функции нагрузки в резистивных цепях, используются в качестве делителя напряжения (см. рисунок ниже) и тока, являются элементами фильтров, применяются для формирования импульсов, выполняют функции шунтов и многое другое. Сегодня трудно себе представить электрическую схему, в которой не задействованы несколько резистивных элементов.
Без резисторов не работает ни один электронный прибор.
Устройство и принцип работы
Конструкция постоянных резисторов довольно простая. Они состоят из керамической трубки, поверх которой намотана проволока или нанесена резистивная плёнка с определённым сопротивлением. На концы трубки вставлены металлические колпачки с припаянными выводами для поверхностного монтажа. Для защиты слоя используется лакокрасочное покрытие.
Устройство таких элементов можно понять из рисунка 2 ниже.
В большинстве моделей такая конструкция традиционно сохраняется, но сегодня существуют различные виды сопротивлений с использованием резистивного материала, устройство которых немного отличается от конструкции описанной выше.

Современную электронную аппаратуру наполняют платы, начинённые миниатюрными деталями. Поскольку тенденция к уменьшению размеров электронных приборов сохраняется, то требования к уменьшению габаритов коснулись и резисторов. Для этих целей идеально подходят непроволочные сопротивления. Они просты в изготовлении, а их номинальные мощности хорошо согласуются с параметрами маломощных цепей.
Казалось бы, что эра проволочных резисторов постепенно уходит в прошлое. Однако это не так. Спрос на проволочные сопротивления остаётся в тех сферах, где транзисторы с металлоплёночным или с композитным резистивным слоем не справляются с мощностями электрических цепей.
Для непроволочных резисторов используются следующие резистивные материалы:
Перечисленные вещества обладают высокими показателями удельного сопротивления. Это позволяет изготавливать электронные компоненты с очень маленькими корпусами, сохраняя при этом значения номинальных величин.
Размеры и формы корпусов, проволочных выводов современных резисторов соответствуют стандартам, разработанным для автоматической сборки печатных плат. С целью надёжного соединения выводов способом пайки, выводы деталей проходят процесс лужения.
Конструкция регулировочных (рис. 3) и подстроечных резисторов (рис.4) немного сложнее. Эти переменные транзисторы состоят из кольцевой резистивной пластины, по которой скользит бегунок. Перемещаясь по кругу, подвижный контакт изменяет расстояние между точками на резистивном слое, что приводит к изменению сопротивления.


Принцип действия.
Подбирая резисторы соответствующего номинала, можно изменять на участках цепей величины тока и напряжения. Например, увеличивая сопротивление последовательно включённого резистора на участке цепи, можно пропорционально уменьшить силу тока.
Условно резистор можно представить себе в виде узкого горлышка на участке трубки, по которой течёт некая жидкость (см. рис. 5). На выходе из горлышка давление будет ниже, чем на его входе. Примерно, то же самое происходит и с потоком заряженных частиц – чем больше сопротивление, тем слабее ток на выходе резистора.

Мы уже упомянули два типа резисторов, отличающиеся по конструкции: постоянные, у которых сопротивление статичное (допускается мизерное отклонение параметров при нагреве элемента) и переменные. К последним можно добавить подвид переменных сопротивлений (полупроводниковых резисторов) – нелинейные.
Сопротивление нелинейных компонентов изменяется в широких пределах под воздействием различных факторов:
За видом резистивного материала классификация может быть следующей:
Отличие плёночных smd компонентов от композиционных деталей состоит в способах их изготовления. Композиционные детали производятся путём прессования композитных смесей, а плёночные – путём напыления на изоляционную подложку.
В интегральных монокристаллических микросхемах методом трафаретной печати или способом напыления в вакууме создают встроенные интегральные резисторы.
По назначению сопротивления подразделяются на детали общего назначения и на компоненты специального назначения:
Можно классифицировать детали и по другим признакам, например по типу защиты от влаги или по способу монтажа: печатный либо навесной.
Номиналы резисторов
Элементы имеют свой допуск в отклонениях номинальных сопротивлений. В соответствии с допусками номиналы резисторов разбиты на 3 ряда, которые обозначаются: Е6, Е12, и Е24.
Компоненты ряда Е6 имеют допуск отклонения ± 20%; ряда Е12 – ± 10%, а ряда Е24 – ± 5%.
Номиналы резисторов каждого ряда представлены в справочных таблицах, которые можно найти в интернете.
Маркировка
Раньше на корпусах сопротивлений проставляли номинал, ряд, мощность и серийный номер. В связи с миниатюризацией деталей перешли на цветовую маркировку. Параметры сопротивлений кодируют с помощью цветных колец (см. рис. 8).
Если на корпусе присутствует 3 кольца, то первые два обозначают величину сопротивления, третье – множитель, а допустимое отклонение составляет 20%.
Если на корпусе 4 кольца, то значения первых трёх из них такие же, как в предыдущем примере, а четвёртое кольцо указывает на величину отклонения.
Пять колец: первые 3 указывают величину сопротивления, на четвёртой позиции – множитель, а на пятой – допуск.
На сверхточных деталях наносятся 6 цветовых полос: три первых указывают величину сопротивления, полоса на четвёртой позиции – множитель, а пятое кольцо — допустимое отклонение.
Каждому цвету присвоена конкретная цифра (от 0 до 9). Учитывая позицию кольца и его цвет, можно с точностью определить параметры изделия. Для этого удобно пользоваться таблицей цветов (рис. 9).

В некоторых случаях вместо сопротивления используют обычные перемычки. Считается что у них нулевое сопротивление. Вместо перемычек иногда устанавливают резистор с нулевым сопротивлением (по сути та же перемычка, только адаптирована под размеры резистора). На корпус такого сопротивления наносят 1 чёрную полоску.
Маркировка SMD-резисторов
Сопротивления, предназначенные для поверхностного монтажа маркируют цифрами (см. рис. 10). Кодировка сложна для запоминания. В ней учитывается количество цифр и их позиции. Цифрами кодируют типоразмеры изделий и значения основных параметров. Для расшифровки кодов данного типа маркировки существуют справочные таблицы или калькуляторы.

Код на рисунке расшифровывается так: номинальное сопротивление 120×10 6 Ом (последняя цифра показывает количество нулей, то есть степень числа 10). Резистор из ряда Е96 с допуском 1%, типоразмер 0805 либо 1206 (значения, выделенные курсивом, определяются по справочнику).
Обозначение на схемах
Традиционно резисторы на схемах обозначают в виде прямоугольника (по ГОСТ 2.728-74) или ломаной линии (рис. 12 — в основном на схема западного образца). В прямоугольнике иногда указывают мощность, используя для этого условные обозначения в виде вертикальных, косых или горизонтальных чёрточек (см. рисунок ниже):
Возле значка проставляют букву R и номинал резистора.

В отличие от постоянных деталей, обозначение переменных резисторов имеет особенность: над прямоугольником добавляется стрелка, указывающая, что в конструкции детали есть скользящий контакт (бегунок).
Например, УГО потенциометра выгляди так:
Характеристики и параметры
Пределы границ сопротивлений для деталей общего назначения находятся в промежутке от 10 Ом до 10 МОм. Для таких компонентов номинальная мощность рассеивания составляет 0,125 – 100 Вт.
Сопротивление высокоомных деталей составляет порядка 10 13 Ом. Такие изделия применяются в измерительных устройствах, предназначенных для малых токов. Величины номинальных мощностей на корпусах таких компонентов могут не указываться. Рабочее напряжение от 100 до 300 В.
Класс высоковольтных деталей предназначен для работы под напряжением 10 – 35 кВ. Их сопротивление достигает 10 11 Ом.
Для высокочастотных резисторов важен номинал рабочей частоты. Они способны работать на частотах свыше 10 МГц. Высокочастотные токи сильно нагревают детали. При интенсивном охлаждении номинальные мощности таких компонентов достигают величин 5, 20, 50 кВт.
В точных измерительных и вычислительных устройствах, а также в релейных системах применяются прецизионные резисторы. Они обладают высокой стабильностью параметров. Мощность рассеивания у таких деталей не превышает 2 Вт, а номинальное сопротивление лежит в пределах 1 – 10 6 Ом.
Кроме основных характеристик иногда важно знать уровень напряжений шума, зависимость сопротивления реальных резисторов от нагревания (температурный коэффициент сопротивления) и некоторые другие.
Соединение резисторов
Сопротивления можно соединять двумя способами – параллельно либо последовательно.
Для расчета последовательно и параллельно соединенных резисторов удобно воспользоваться нашими калькуляторами: