Сечение как строить геометрия

Сечение как строить геометрия

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

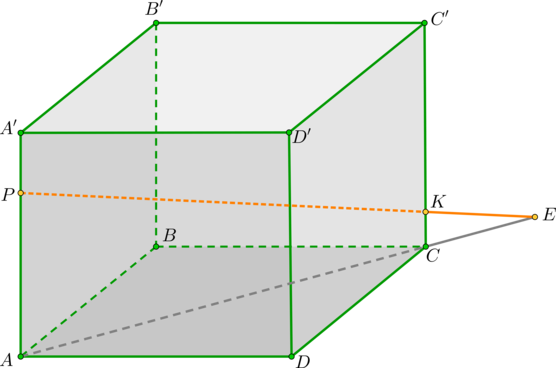
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

.

Соединим точки P и L ( они лежат в одной плоскости).

.

Источник

Учимся строить сечения многогранников. Часть 2.

Учимся строить сечения многогранников. Часть 2.

Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.

Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.

В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.

Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.

Постройте сечения, проходящие через точки .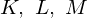

Задание 1:

Источник

Методы построения сечений многогранников

Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

Источник

Построение сечений

Определение

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

3. Прямая и плоскость параллельны, если они не имеют общих точек.

4. Две плоскости параллельны, если они не имеют общих точек.

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Важные теоремы

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

7. Теорема о трех перпендикулярах.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Замечание

Еще один важный факт, часто использующийся для построения сечений:

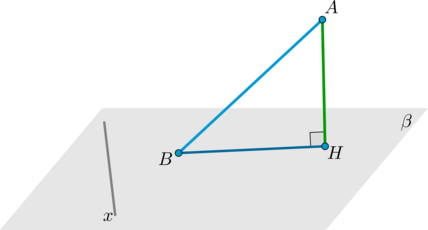
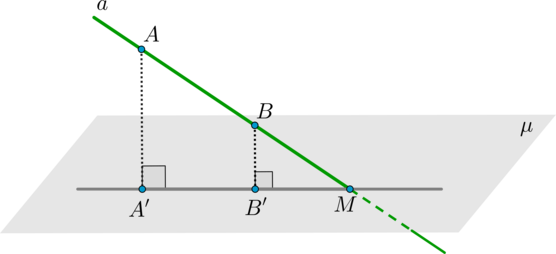
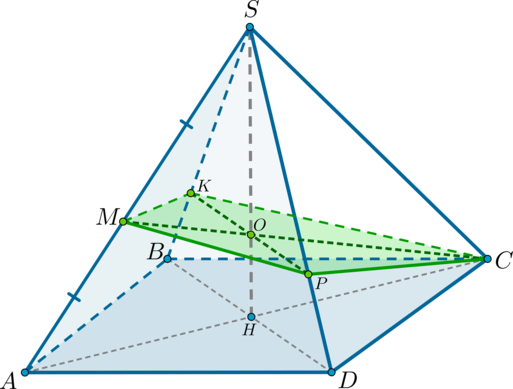
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

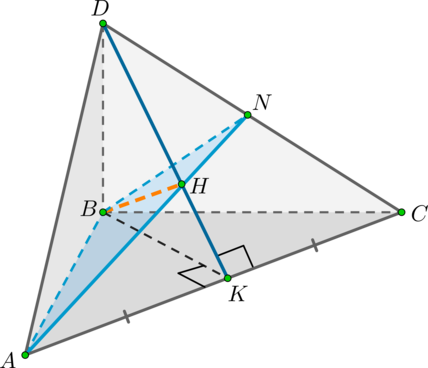
Причем заметим, что все точки \(A, B, A’, B’, M\) лежат в одной плоскости.

Пример 1.

Решение

Пример 2.

Решение

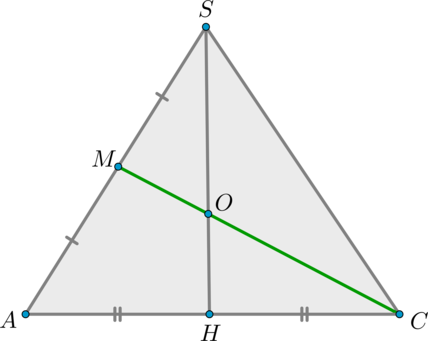
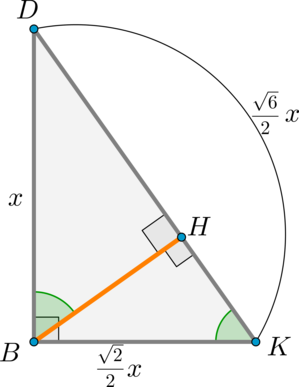
а) \(\triangle AMQ\sim \triangle ADO\) по двум углам ( \(\angle Q=\angle O=90^\circ, \ \angle A\) – общий). Значит,

\[\dfrac=\dfrac=\dfrac=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1<\sqrt3>a\]

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\) ).

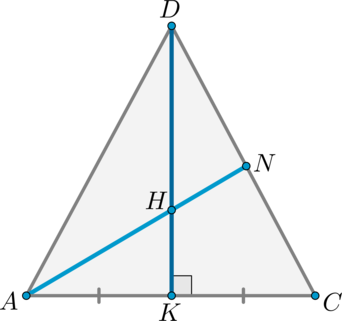
Пример 3

Решение

Пример 4

Решение

\[\dfrac=\dfrac \Rightarrow DH=\dfrac<\sqrt6>3x \Rightarrow HK=\dfrac<\sqrt6>6x \Rightarrow DH:HK=2:1\]

Источник

Сечение как строить геометрия

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

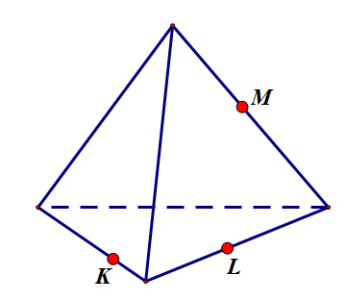
Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

Теоремы, используемые при построении сечений

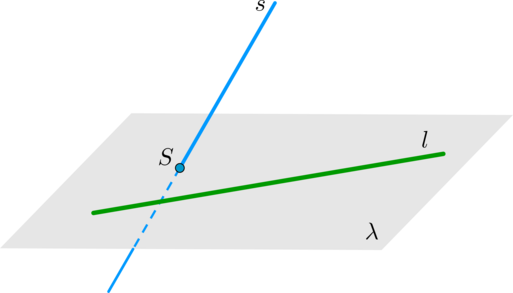
Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.

Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости

Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.

Алгоритм построения сечений

Для построения сечений рекомендуем пользоваться следующим алгоритмом.

1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.

2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.

3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.

Для контроля правильности построенного сечения, проверяйте, что:

– все вершины сечения лежат на рёбрах многогранника;

– все стороны сечения лежат в гранях многогранника;

– в каждой грани многогранника лежит не более одной стороны сечения.

Источник