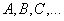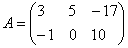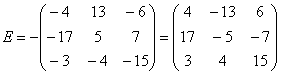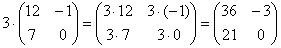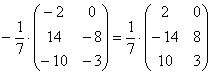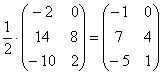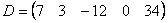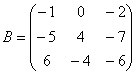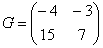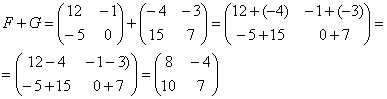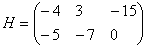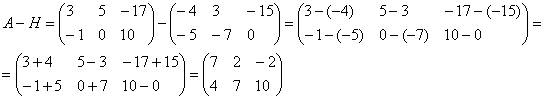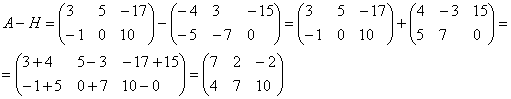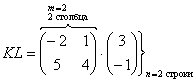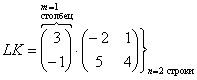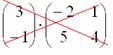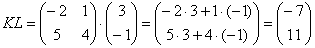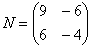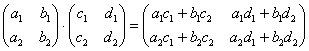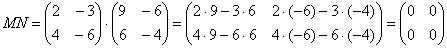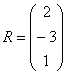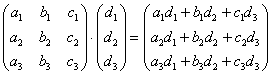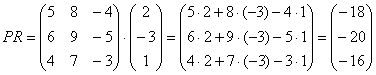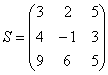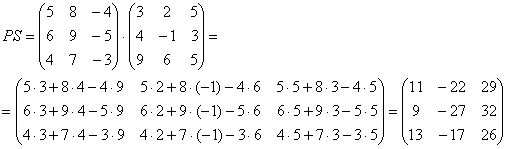Сложение матриц как решать

Математика для чайников. Матрицы и основные действия над ними

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Источник

Действия с матрицами

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов: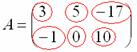

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: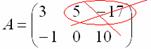

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки: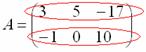

и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 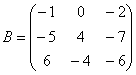– матрица «три на три».

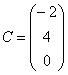
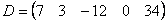
Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: 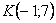. По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице 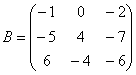. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: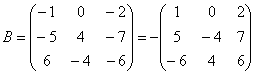

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: 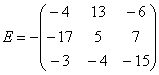. Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

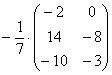
Сначала рассмотрим то, чего делать НЕ НАДО: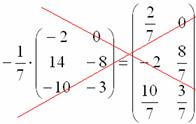

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 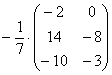– окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В этом случае можно и НУЖНО умножить все элементы матрицы на 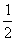, так как все числа матрицы делятся на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

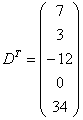
Транспонированная матрица обычно обозначается надстрочным индексом 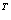или штрихом справа вверху.

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Сложить матрицы 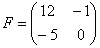и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Найти разность матриц ,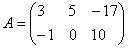

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :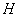

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

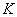
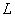
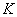
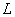
Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
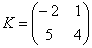
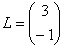
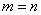
Можно ли умножить матрицу на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно:

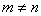
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
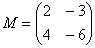
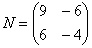
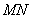
Например, для матриц, и возможно как умножение , так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

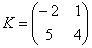
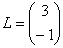
Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:

– попытайтесь сразу уловить закономерность.

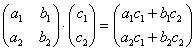
Умножить матрицу 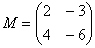на матрицу

Формула:

В результате получена так называемая нулевая матрица.

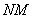
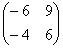
Попробуйте самостоятельно выполнить умножение (правильный ответ ).

Обратите внимание, что 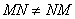! Это почти всегда так!

Таким образом, при умножении переставлять матрицы нельзя!

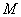
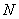
Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу 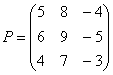на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу 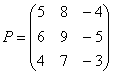на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.

А пока спектакль закончен.

После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

Знакомство с матрицами

Понятие и базовые операции.

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.

Что такое матрица

Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.

Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.

Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.

В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.

В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.

Общая схема матрицы Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три

Простые операции с матрицами

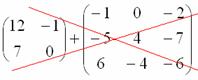
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число

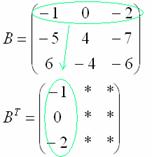
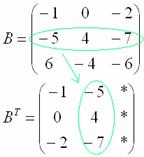
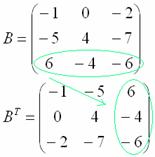
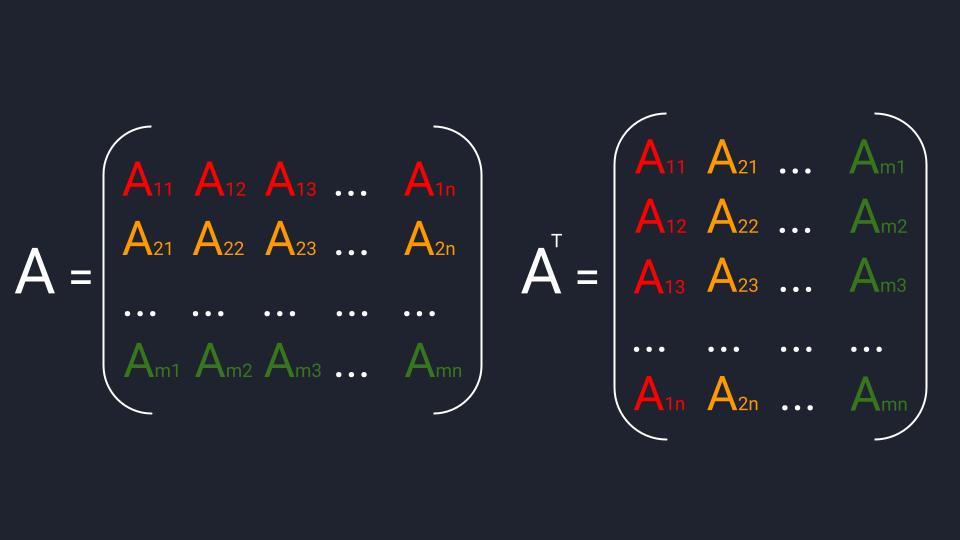
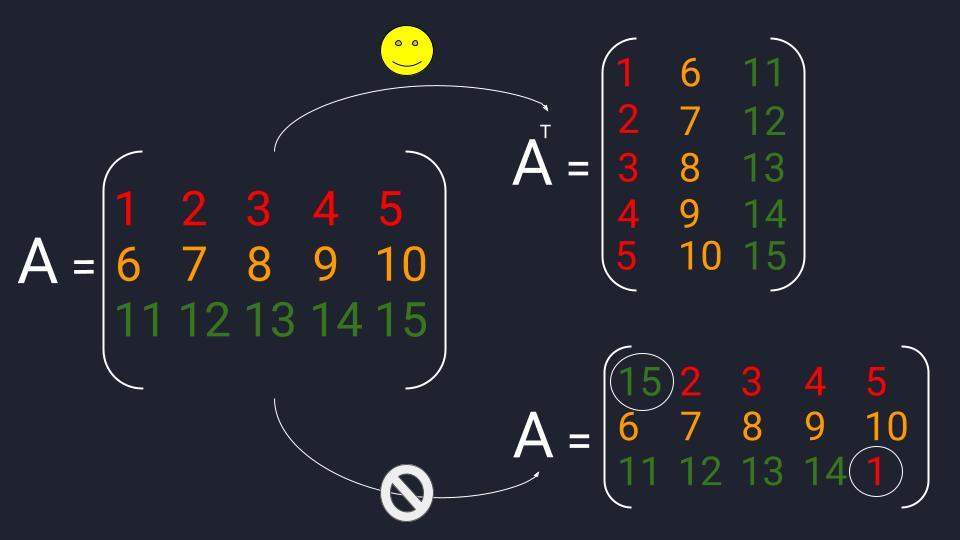
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.

⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.

Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матриц

Умножение матриц

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2

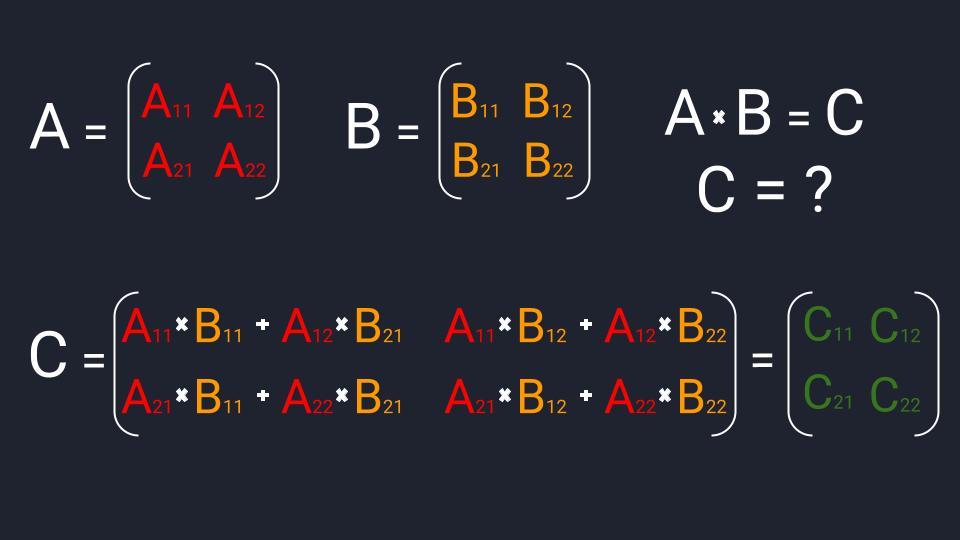
Что дальше

В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽

Источник