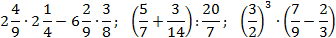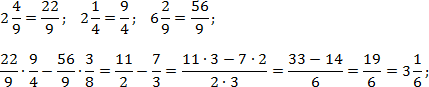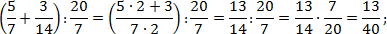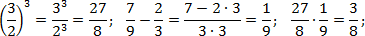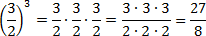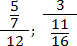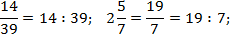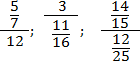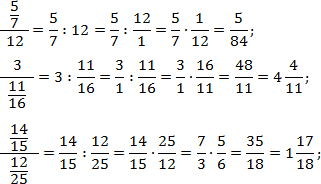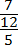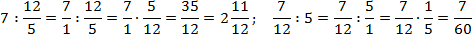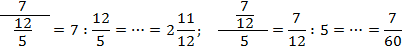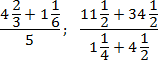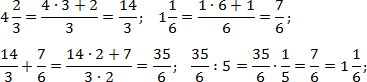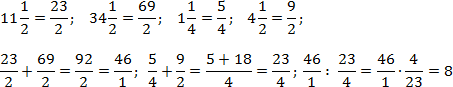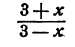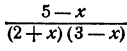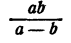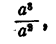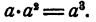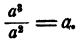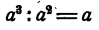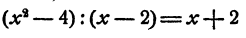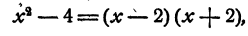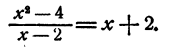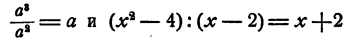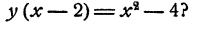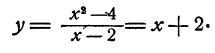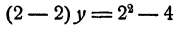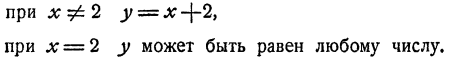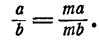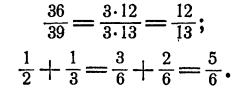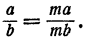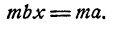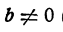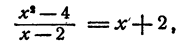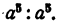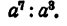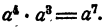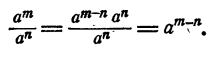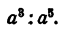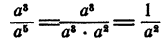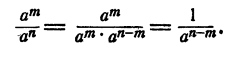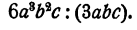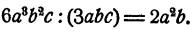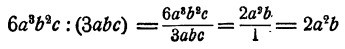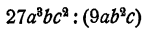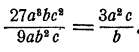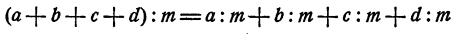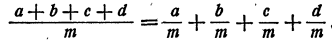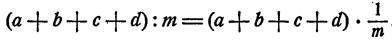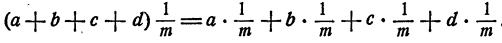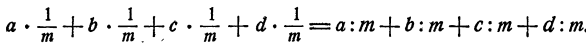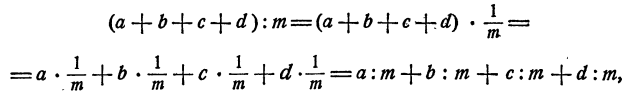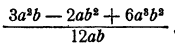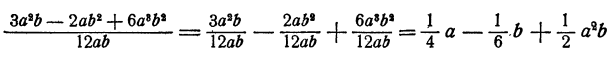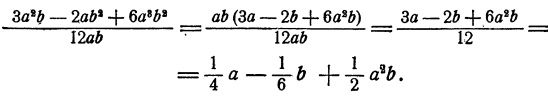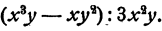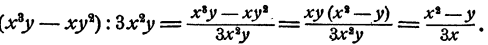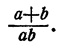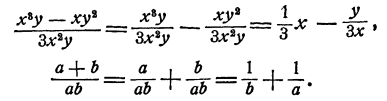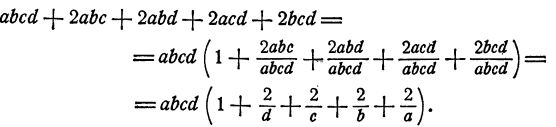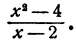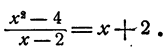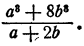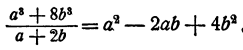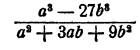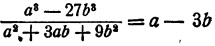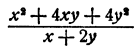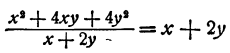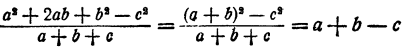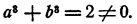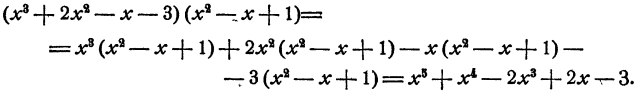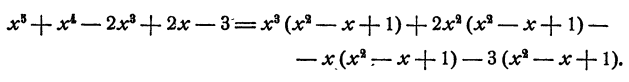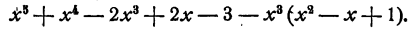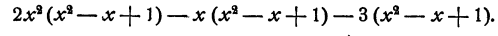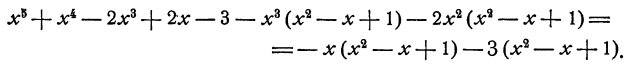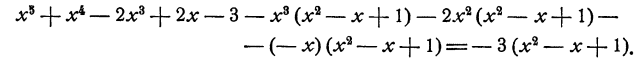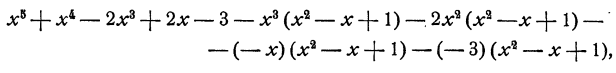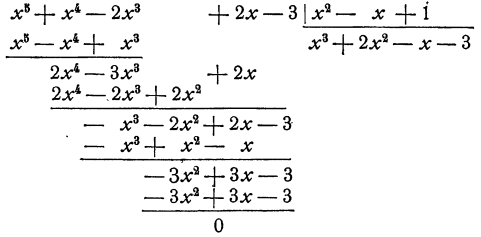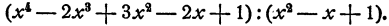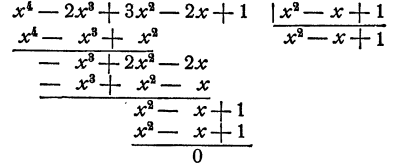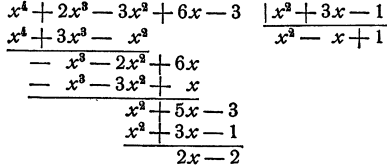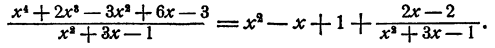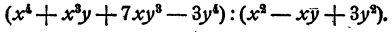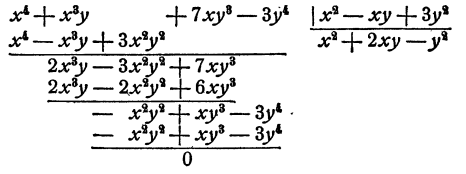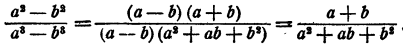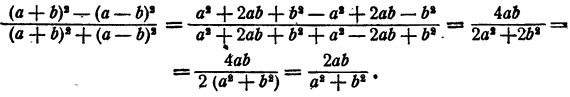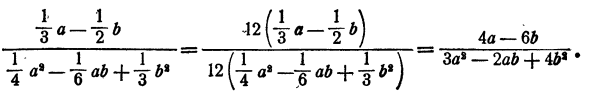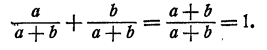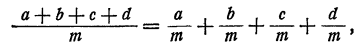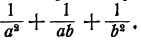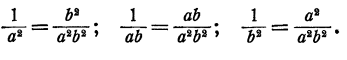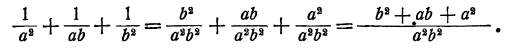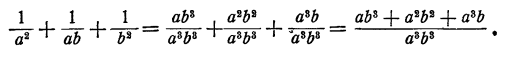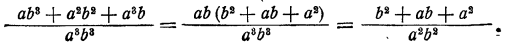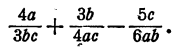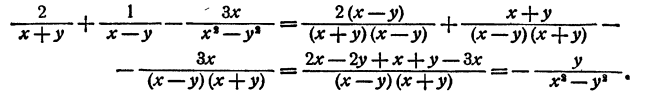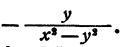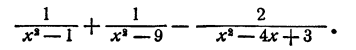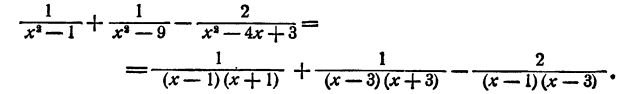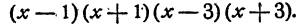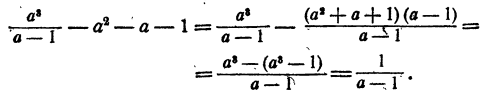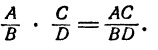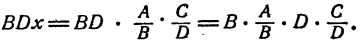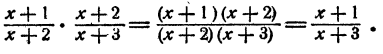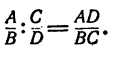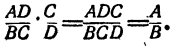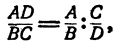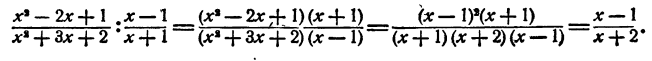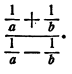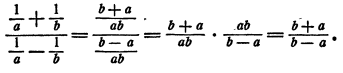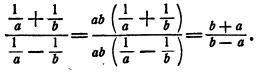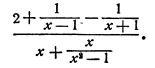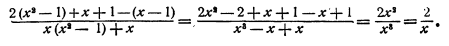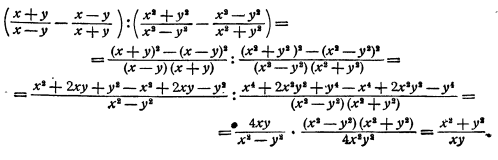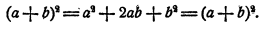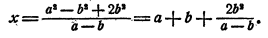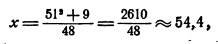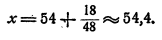Составная дробь как решать

Дроби обыкновенные правильные и неправильные, смешанные и составные.

Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.

Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби – над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой – в нижней части). Обыкновенные дроби, в свою очередь делятся на: правильные и неправильные, смешанные и составные. Обыкновенные дроби тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).

или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:

Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной:

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Число, содержащее целую и дробную части, называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью. Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).

К подобному виду обычно и приводят смешанные дроби.

Составные дроби.

Многоэтажной, или составной дробью является дробь, которая содержит в себе несколько горизонтальных (либо реже — наклонных) черт:

либо либо .

Источник

Сложные выражения с дробями. Порядок действий

Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?

В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:

Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.

Задача. Найдите значения выражений:

Переведем все дроби из первого выражения в неправильные, а затем выполним действия:

Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.

Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:

Многоэтажные дроби

До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.

Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:

Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:

Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:

Задача. Переведите многоэтажные дроби в обычные:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Получаем:

В последнем примере перед окончательным умножением дроби были сокращены.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

Это выражение можно прочитать по-разному:

Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

Задача. Найдите значения выражений:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

Источник

Математические дроби – просто о сложном

В статье описаны математические дроби: основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями (сокращение, приведение, сравнение, сложение, вычитание, умножение и деление).

Дробь и ее виды

Правильная — дробь, у которой числитель меньше знаменателя (например, 1/5, 2/9).

Неправильная — дробь, у которой числитель больше или равен знаменателю (например, 7/2, 5/5).

Смешанная — дробь, записанная в виде целого числа и правильной дроби. Она представляет собой сумму этого числа и дроби. Любую неправильную дробь можно перевести в смешанную путем выделения целой части (например, 9/4 = 2 ¼).

Десятичная — дробь со знаменателем 10, 100, 1000 и т.д. (например, 7/10 или 0,7; 9/100 или 0,09). Десятичная дробь записывается в виде целой и дробной части, которые отделяются запятой.

Математические дроби: основное свойство

Если числитель и знаменатель умножить или разделить на одинаковое число (не ноль), то получится равная дробь. Например, 2/3 = 2*2 / 3*2 = 4/6

Сокращение дроби

Сокращение осуществляется с помощью основного свойства дроби (чтобы упростить ее вид).

Чтобы сократить математические дроби, нужно разделить числитель и знаменатель дроби на НОД.

НОД – это наибольший общий делитель (то есть максимальное число, на которое делится и числитель, и знаменатель). Например, для дроби 4/20 наименьшим общим делителем будет 4 (4/20 = 1/5).

Приведение дробей к общему знаменателю

Любые две дроби можно привести к общему знаменателю. Обычно дроби приводят к наименьшему общему знаменателю (НОК) – минимальное число, которое делится на каждый знаменатель.

Например, для дробей 1/4 и 1/3 общий знаменатель общий знаменатель равен 12, для дробей 1/6 и 1/3 общий знаменатель будет 6).

Для приведения дроби к общему знаменателю нужно:
1. Найти общий знаменатель – НОК (для дробей 1/6 и 1/9 общий знаменатель будет равен 18);
2. Найти множитель для каждой дроби – разделить общий знаменатель на знаменатель исходной дроби (для дроби 1/6 множитель будет равен 3 (18:6=3), для дроби 1/9 – 2 (18:9=2)).
3. Умножить числитель дроби на множитель (для дроби 1/6 получаем 1*3/6*3=3/18, для дроби 1/9 получаем 2*1/2*9=2/18)

Преобразование неправильной дроби в смешанную дробь и обратно

Любую неправильную дробь можно перевести в смешанную (рассмотрим на примере 14/3).
Для перевода необходимо выполнить деление числителя на знаменатель с остатком (14 разделить на 3 равно 4 и остаток 2): получавшаяся целая часть от деления (число 4) – целая часть дроби, остаток от деления (число 2) – числитель правильной дроби. Получаем число 4 2/3.
На примере пирога: каждый пирог разрезан на 3 части и всего есть 14 кусочков. Получаем, что 12 кусочков составляют 4 целых пирога и еще остается два кусочка).

Для перевода смешанной дроби в неправильную необходимо (рассмотрим на примере 4 2/3):
для получения числителя целую часть дроби умножить на знаменатель и прибавить исходный числитель (4 умножить на 3 и прибавить 2, получим 14); знаменатель оставить прежним (число 3).
На примере пирога: есть 4 целых пирога, разрезанных на 3 части, и еще 2 кусочка из трех; получаем 12 кусочков из пирогов, разрезанных на три части, и 2 кусочка из пирога, разрезанного на три части. Итого, получаем 14 кусочков пирогов, каждый из которых разрезан на три части.

Математические дроби: сравнение

Если сравнивать две математические дроби с одинаковыми знаменателями, то больше та дробь, числитель которой больше (например, 5/6 > 1/6, то есть пять частей из шести будет больше, чем одна часть из шести).

Если сравнивать две математические дроби с одинаковыми числителями, то больше та дробь, знаменатель которой меньше (например, 1/2 > 1/3, то есть 1/2 часть пирога будет больше, чем 1/3).

Чтобы сравнить две обыкновенные дроби, следует привести дроби к общему знаменателю и сравнить числители получившихся дробей (например, для сравнения 3/4 и 5/6 нужно привести дроби к общему знаменателю; получаем 9/12

Для отправки комментария вам необходимо авторизоваться.

Источник

Преобразование дробных алгебраических выражений с примерами решения и образцами выполнения

Особенность дробных выражений:

Алгебраическое выражение называется дробным, если в числе указанных в нем действий есть деление на выражение, содержащее буквы. Это является причиной некоторых особенностей дробных алгебраических выражений по сравнению с выражениями целыми.

Мы знаем, что действия сложения, вычитания и умножения выполнимы всегда, каковы бы ни были числа, над которыми производятся эти действия. Поэтому и всякое целое алгебраическое выражение имеет смысл при всевозможных численных значениях входящих в него букв. Иначе обстоит дело с выражениями дробными. Из-за того, что деление на нуль невозможно, всякое дробное выражение не имеет смысла при таких значениях букв, при которых знаменатель обращается в нуль.

теряет смысл при x = 3. При всех, остальных значениях х это выражение имеет смысл, ибо 3 — х обращается в нуль только при х = 3.

Точно так же выражение

теряет смысл при х = — 2 и при х=3, а при всех остальных значениях для х имеет смысл.

теряет смысл при а = b и имеет смысл при любых неравных значениях а и b и т. д.

Рассмотрим, наконец, следующее алгебраическое выражение:

или, что то же самое,

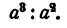
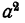
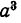
По смыслу действия деления, есть такое число, которое, будучи умножено на дает . Очевидно, что таким числом является а, ибо

Однако, это равенство верно не при всех численных значениях а. Именно, если а = 0, то правая часть равенства есть 0, а левая превращается в выражение 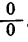Это выражение, как мы уже видели, приходится рассматривать как не имеющее смысла.

оказывается верным при всех значениях а, кроме значения а = 0.

Точно так же равенство

верно при всех значениях х, кроме x = 2. Действительно,

и следовательно, по определению деления, если 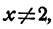то

А при х=2 левая часть равенства теряет смысл.

Как было сказано раньше, тождеством называется равенство двух выражений, верное при всех допустимых значениях входящих в него букв, причем под допустимыми значениями понимаются такие, при
которых оба сравниваемых выражения имеют смысл.

В силу этого определения равенства

следует рассматривать как тождества. Однако при тождественных преобразованиях с дробными выражениями необходимо помнить о том, что при Тех значениях букв, при которых одна или обе части
равенства теряют смысл, и все «тождество» превращается в равенство, лишенное смысла. Особенно важно помнить об этом в случае, когда дробное выражение получается в результате решения какой-либо задачи. В этом случае необходимо подвергнуть отдельному исследованию такие числовые значения для букв, при которых дробное выражение теряет смысл.

Пример:

При каких значениях у имеет место равенство

Решение:

Очевидно, что у находится посредством действия деления. Именно,

Форма ответа у = х + 2 такова, что при любом значении числа х у получает вполне определенное значение. Так, при x = 0 y = 2; при х=1 y= 3 и т. д. В частности, при х = 2 у = 4.

Однако последнее утверждение неточно. Действительно, при х — 2 наше равенство превращается в такое:

или 0y = 0, верное при любом значении y, а не только при у = 4. Поэтому точный ответ на поставленный вопрос будет такой:

Основное свойство дроби

При преобразованиях дробных алгебраических выражений постоянно приходится пользоваться следующим основным свойством дроби.

Значение дроби не изменяется, если числитель и знаменатель умножить на одно и то же число, отличное от нуля.

В буквенной записи это свойство выглядит так: при любом 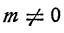имеет место равенство

Читая это равенство справа налево, мы приходим к следующему правилу: любой общий множитель числителя и знаменателя дроби может быть сокращен.

Это свойство в обеих формулировках в применении к численным дробям хорошо известно и широко пользуется при действиях над дробями. В первой формулировке — при приведении дробей к общему знаменателю, во второй — при сокращении дробей. Например,

В первом примере мы произвели сокращение дроби на 3, во втором для приведения дробей к общему знаменателю мы умножили числитель и знаменатель первой дроби на 3, второй дроби на 2.

В арифметике это свойство используется в применении к дробям, числитель и знаменатель которых — целые числа, и к множителям, также являющимися целыми числами. В алгебре под буквами понимаются любые числа: целые и дробные, положительные и отрицательные. Поэтому в алгебраической дроби числитель и знаменатель, даже если они имеют вид целых алгебраических выражений, могут принимать не только целые, но и дробные значения. Соответственно и множитель тоже может принимать дробные значения.

Поэтому, желая распространить основное свойство дроби на дроби алгебраические, следует его предварительно доказать при самых общих предположениях.

Доказательство основного свойства. Нам нужно доказать, что если 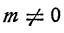,то

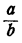
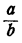
Дробь есть частное от деления числа а на число b, т. е. такое число, которое при умножении на делитель b дает делимое а. Обозначив через х, мы будем иметь равенство bх = а. Умножив обе части этого равенства на любое число m, мы получим снова верное равенство

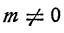
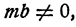
По условию, . Тогда и ибо

(иначе частное 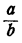не
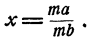
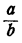
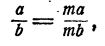
имело бы смысла), а произведение двух не равных нулю чисел не равно нулю. Таким образом, х есть такое число, которое при умножении на не равное нулю число mb дает число mа. Следовательно, по определению действия деления, Но буквой х была обозначена дробь -. Следовательно, что и требовалось доказать.

Деление целых алгебраических выражений

Если требуется разделить одно целое алгебраическое выражение на другое, результат всегда может быть записан в виде дроби, в числителе и знаменателе которой находятся эти выражения. Такие дроби
называются алгебраическими дробями. Однако часто бывает, что частное от деления двух целых алгебраических выражений в свою очередь оказывается целым алгебраическим выражением. В этом случае говорят, что первое выражение делится на второе.

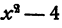
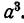
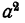
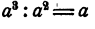
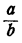
т. е. многочлен делится на многочлен х — 2. Точно так же одночлен делится на так как и т. д. Но одночлен а не делится на одночлен b, так как их частное не может быть записано в виде целого алгебраического выражения.

Понятие делимости в применении к целым алгебраическим выражениям сходно с понятием делимости целых чисел: мы говорим, что одно целое число делится на другое целое число, если их частное есть целое число (например, 6 делится на 2, но 6 не делится на 4 и т. д.). Однако не следует их путать одно с другим. 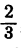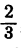Так, например, одночлен 2х делится в алгебраическом смысле на одночлен З х, так как их частное равно одночлену ,т, е. целому алгебраическому выражению. Однако при целых значениях для буквы х число 2х никогда не делится в арифметическом смысле на число Зx, так как частное от их деления есть дробное число .

Цель ближайших параграфов состоит в установлении некоторых приемов деления целых алгебраических выражений и в установлении некоторых признаков, по которым можно узнать, делится или не делится одно данное выражение на другое.

Деление степеней с одинаковыми основаниями

Пример:

Решение:

Без всяких вычислений ясно, что частное равно 1. Такой же результат будет при делении одинаковых степеней с любым показателем.

Пример:

Решение:

Очевидно, что результат равен 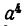, ибо

Результат получен посредством вычитания показателей степени в делимом и делителе на основании того, что при проверке деления умножением показатели складываются.

Правило. При делении степеней с одинаковыми основаниями в предположении, что показатель степени в делимом больше показателя степени в делителе, частное равно степени с тем же основанием и с показателем, равным разности показателей в делимом
и делителе.

Короче: при делении степеней с одинаковыми основаниями показатели вычитаются.

Действительно, если m > n, то

Пример:

Решение:

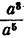
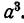
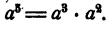
Запишем то же самое в виде дроби и произведем сокращение на , учитывая, чтo Получим

Результат имеет такой же вид при любых показателях степени, если только показатель в делимом меньше показателя в делителе.

Если m

При делении степеней с одинаковыми основаниями мы рассмотрели все три случая, которые могут представиться.

Случай 1. Показатели степени равны.

Случай 1. Показатели степени равны.
Случай 2. Показатель степени в делимом больше показателя степени в делителе.
Случай 3. Показатель степени в делимом меньше показателя степени в делителе.

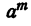
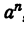
Мы убедились в том, что в первых двух случаях в частном получается целое-алгебраическое выражение. Таким образом, делится на , если m равно n или m больше n. В третьем случае (m Деление одночленов

Пример:

Решение:

Требуется найти такое выражение, которое, будучи умножено на 3аbс, даст 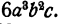Легко найти одночлен, удовлетворяющий этому требованию. Мы знаем, что при умножении одночленов коэффициенты перемножаются, а показатели степени при каждой букве складываются. Поэтому в искомом одночлене коэффициент равен 6 : 3 = 2, буква а должна входить с показателем 3 — 1 = 2, а буква b с показателем 2 —1 = 1, а буква с совсем не должна входить. Таким образом,

Такое же рассуждение можно привести в любом другом случае деления одночлена на одночлен: необходимо только, чтобы все буквы, входящие в делитель, входили и в делимое с не меньшими показателями степени.

Только что отмеченное условие есть условие делимости
одночленов, т. е. условие, при выполнении которого частное от деления одночленов есть целое алгебраическое выражение, именно одночлен.

Мы приходим к следующему правилу.

Чтобы поделить одночлен на одночлен, в случае, если все буквы, входящие в делитель, входят и в делимое с не меньшими показателями, нужно:

Менее подробно: при делении одночленов коэффициенты нужно поделить, а показатели при одинаковых буквах вычесть.

Можно, однако, этим правилом не пользоваться, а сразу записать дробь и произвести возможные сокращения. Рассмотрим тот же пример:

Здесь условие делимости выполнено. Посмотрим теперь, какой вид имеет результат, если условие делимости не выполнено.

Пример:

Решение:

Здесь условие делимости не выполнено, так как буква b входит в делитель в большей степени, чем в делимое. Однако мы можем записать дробь и произвести сокращение. Получим :

Очевидно, что полученное выражение 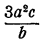не может равняться целому алгебраическому выражению, т. е. многочлену или одночлену, так как произведение одночлена b на любой многочлен (или одночлен) равно
многочлену (или одночлену), содержащему букву b, а 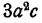буквы b не содержит.

Таким образом, всегда, если только условие делимости не выполнено, частное от деления двух одночленов не является целым алгебраическим выражением. Это частное можно записать только в виде алгебраической дроби.

Деление многочлена на одночлен

Правило умножения многочлена на одночлен было выведено на основании распределительного закона умножения суммы на число. Точно так же правило деления многочлена на одночлен основывается на распределительном законе, видоизмененном применительно к делению. Это в идоизменение выглядит так:

Частное от деления суммы нескольких слагаемых на число равно сумме частных, получающихся при делении каждого слагаемого на то же число.

Запишем это правило в виде формулы:

или при обозначении частного в виде дроби

Докажем эту формулу. Мы знаем, что поделить какое-либо число на число m— это все равно, что умножить его на обратное число 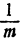Следовательно,

Для умножения суммы на число, в каком бы виде это число ни было выражено, справедлив распределительный закон. Поэтому

А теперь воспользуемся тем, что умножить какое-либо число на 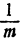все равно, что разделить его на m, т. е.

Соединяя выкладки в одну цепочку равенств, получим

что и требовалось доказать.

Мы сформулировали и доказали правило деления суммы на число для суммы четырех слагаемых. Очевидно, однако, что те же рассуждения можно применить к сумме любого числа слагаемых.

Применим теперь доказанное правило к делению многочлена на одночлен.

Пример:

Решение:

По правилу деления суммы на число имеем

Можно решить этот пример и другим способом, посредством вынесения за скобку:

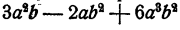
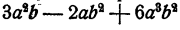
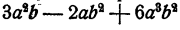
Вынесение за скобку здесь оказывается полезным потому, что само действие вынесения за скобку есть действие деления, но не указанное явно. Действительно, что значит вынести за скобку одночлен ab из многочлена ? Какой многочлен останется в скобке при выполнении этого действия? Очевидно, такой, многочлен, который при умножении на аb дает , т. е:, по определению деления, частное от деления многочлена на одночлен ab.

Ответ,.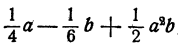

Многочлен делится на одночлен, очевидно, в том и только в том случае, если каждый его член делцтся на этот одночлен.

Если это условие не выполнено, то чаще всего следует
ограничиться записью результата в виде дроби и, если это возможно, произвести сокращение посредством вынесения подходящих множителей в числителе за скобку.

Пример:

Решение:

Пример:

Решение:

В этом примере нельзя произвести сокращение. Поэтому никаких упрощающих преобразований произвести нельзя.

Ответ. Упростить нельзя.

Иногда бывает целесообразно произвести почленное деление многочлена на одночлен и в случае, если отдельные члены многочлена на этот одночлен не делятся. При этом в результате получается сумма нескольких слагаемых, часть которых (или все) имеют вид дробей.

Рассмотрим преобразование такого типа для двух последних примеров

Повторяем, что такого рода преобразования применяются сравнительно редко. Еще реже применяется вынесение за скобку одночлена так, что при этом в скобке получается сумма дробей. Но все же
иногда такое преобразование бывает нужно.

Пример:

Мы вынесли abcd за скобку. При этом в скобке остается частное от деления данного многочлена на abcd. После выполнения возможных сокращений в скобке получилась сумма очень простых дробей, так что все алгебраическое выражение стало проще на вид. Однако мы его несколько «испортили». В первоначальной записи оно было целым и имело смысл при всех значениях букв а, b, с, d. В новой записи появились дроби, и теперь выражение не имеет смысла, если
хотя бы одна буква принимает значение, равное нулю.

Применение формул сокращенного умножения к делению многочлена на многочлен

Формулы сокращенного умножения могут быть применены и к делению многочлена на многочлен. Действительно, действие деления заключается в том, что находится один из множителей, если задан
второй и их произведение. Частное есть такое число или алгебраическое выражение, которое, будучи умножено на делитель, дает делимое. Если делимое имеет вид результата какой-либо из формул сокращенного умножения, а делитель имеет вид одного из множителей в той же формуле, то частное равно другому множителю. Рассмотрим несколько примеров.

Пример:

Решение:

Здесь делимое есть разность квадратов двух чисел х и 2, а делитель есть разность первых степеней тех же чисел. Следовательно, частное равно их сумме

Пример:

Решение:

Здесь делимое есть сумма кубов чисел а и 2b,
делитель равен сумме этих чисел. Поэтому частное есть неполный квадрат их разности

Пример:

Решение:

Здесь делимое есть разность кубов а и 3b, делитель — неполный квадрат суммы тех же чисел. Следовательно,

Пример:

Решение:

Делимое есть квадрат суммы чисел х и 2у, т. е.
произведение двух множителей, каждый из которых равен сумме чисел х и 2у. Делитель равен просто сумме этих чисел. Следовательно,

Пример:

Общие замечания о делении многочлена на многочлен

Частное от деления многочлена на многочлен иногда оказывается равным многочлену, но чаще оказывается дробным алгебраическим выражением, которое не может быть преобразовано в целое — в многочлен или одночлен. В первом случае говорят, что многочлен,
являющийся делимым, делится на многочлен, являющийся делителем. Во втором — что не делится.

Укажем некоторые признаки, по которым можно узнать, что делимость не имеет места.

Первый признак. Если степень делимого относительно какой-нибудь буквы меньше степени делителя относительно той же буквы, то частное не может быть целым алгебраическим выражением.

Например, 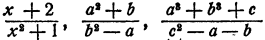не могут быть
представлены в виде целых алгебраических выражений — одночленов или многочленов.

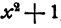
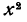
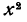
Докажем это для первого примера. Допустим, что частное является многочленом или одночленом. Тогда этот многочлен (или одночлен), будучи умножен на должен равняться x + 2, и следовательно, его старший член, умноженный на должен равняться х. Но это невозможно, так как произведение на любой одночлен содержит х в степени, показатель которой не меньше 2.

Такое же рассуждение можно привести для любых рациональных дробей, зависящих от одной буквы, если степень числителя меньше степени знаменателя. Доказательство Для дробей, зависящих более чем от одной буквы, несколько сложнее из-за того, что членов,
содержащих наивысшую степень выбранной буквы, может быть несколько.

Второй признак. Если существуют такие численные значения для букв, при которых делитель обращается в нуль, а делимое не обращается в нуль, то частное не может быть целым алгебраическим выражением.

Дробь 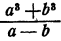нельзя представить в виде целого выражения, так как, например, при а = 1 и b = 1 a — b = 0, но

Совершенно строгое доказательство второго признака не очень просто и требует довольно глубокого исследования свойств алгебраических тождеств.

Деление многочленов, зависящих от одной буквы

Возьмем два многочлена 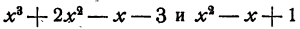и умножим их, пользуясь первым правилом умножения многочлена на многочлен. Получим

Запишем результат в следующей форме:

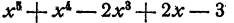
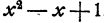
Теперь представим себе, что перед нами поставлена обратная задача. Даны многочлены и .Требуется определить их частное.

В рассматриваемом примере эта задача уже решена, частное равно 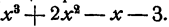Выясним теперь некоторые свойства членов частного, при помощи которых мы смогли бы определить их последовательно один за другим, если бы частное нам не было известно.

Прежде всего старший член частного при умножении на старший член делителя дает старший член делимого. Далее, составим разность

Эта разность, очевидно, равна

Отсюда мы можем заключить, что произведение второго члена частного на старший член делителя равно старшему члену составленной разности.

Составим следующую разность:

Из этого равенства мы заключаем, что третий член частного при умножении на старший член делителя дает старший член составленной разности.

Наконец составим еще одну разность

Из этого равенства мы заключаем, что четвертый член частного при умножении на старший член делителя дает старший член последней составленной разности.

Если мы составим тем же способом следующую разность:

то она окажется равной нулю.

Составление разностей и последовательное вычисление членов частного удобно производить по следующей схеме, напоминающей схему деления многозначных чисел:

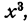
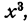
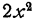
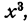
Мы делим старший член делимого на старший член делителя, и результат записываем в частное. Затем умножаем делитель на члены получившегося произведения подписываем под подобными членами делимого и вычитаем из делимого. Старший член полученной разности делим на старший член делителя, и полученное частное добавляем к ранее вычисленному члену . Умножаем делитель на
полученное произведение подписываем под первой разностью и вычитаем из нее. Старший член второй разности делим на старший член делителя, и полученное частное — х принимаем за третий член частного. Делитель умножаем на — х и вычитаем из предшествующей разности. Старший член полученной разности делим на старший член делителя, частное —3 принимаем за четвертый член частного. При следующем вычитании получается разность, равная нулю.

По такой же схеме можно производить деление многочленов всегда, если только деление выполнимо. Заметим только, что при вычислении разностей нет необходимости выписывать все члены делимого, их следует, записывать по мере появления подобных членов в вычитаемых многочленах.

Рассмотрим еще один пример

Действуем по описанной схеме

Однако может случиться, что делимое не делится на делитель. Рассмотрим пример этого рода:

Мы продолжали деление до тех пор, пока это было возможно, именно, пока степень разности не оказалась меньше степени делителя. Эта последняя разность называется остатком от деления данных
многочленов. Степень остатка меньше степени делителя. Многочлен, записанный на месте частного, называется неполным частным от деления данных многочленов.

Очевидно, что для получения полного частного нужно к неполному частному добавить частное от деления остатка на делитель. Таким образом,

или в другой записи

При записи, частного от деления двух многочленов в виде дроби неполное частное называется также целой частью дроби.

Связь между делимым, делителем, неполным частным и остатком может быть выражена и по-другому. Именно, по смыслу вычислений, остаток равен разности при вычитании из делимого произведения
делителя на неполное частное.

Следовательно, делимое равно произведению делителя на неполное частное плюс остаток.

Указанная схема дает возможность выяснить, делится данный многочлен на другой данный многочлен или нет. Делимость имеет место в том и только в том случае, если остаток равен нулю.

Схема деления применима и к делению многочленов, зависящих от нескольких букв. Для того чтобы пользоваться ею в этом случае, нужно расположить делимое и делитель по степеням какой-либо буквы, выбранной в качестве главной.

Пример:

Решение:

Сокращение алгебраических дробей

Частное от деления двух целых алгебраических выражений называется алгебраической дробью. Часто бывает возможно упростить алгебраическую дробь посредством, сокращения общих множителей числителя и знаменателя. Мы уже это делали в § 5, 6 при упрощении частного от деления одночлена на одночлен и. многочлена на одночлен. В случае, если числитель и знаменатель дроби являются многочленами, для сокращения дроби нужно разложить числитель и знаменатель на множители.

Если окажется, что числитель и знаменатель имеют общие множители, то можно их сократить. Если общих множителей нет, то упрощение дроби посредством сокращения невозможно.

Пример:

Пример:

Здесь нам удалось сократить только численный множитель.

Упрощение алгебраической дроби с дробными коэффициентами

Если числитель и знаменатель рациональной дроби являются многочленами с дробными коэффициентами, то для упрощения целесообразно умножить числитель и знаменатель на общий знаменатель всех коэффициентов. Это можно сделать в силу основного свойства дроби.

Пример:

Сложение и вычитание алгебраических дробей

Для того чтобы сложить или вычесть дроби с одинаковыми знаменателями, нужно сложить или вычесть их числители, оставив знаменатель без изменения. Например,

Это следует из распределительного закона, примененного к частному от деления алгебраической суммы на число

прочитанного справа налево.

Если же знаменатели различны, дроби нужно предварительно привести к одному знаменателю. В качестве общего знаменателя можно взять любое общее кратное знаменателей данных дробей, т. е. любой многочлен, делящийся на каждый из этих знаменателей. В частности, за общий знаменатель можно принять произведение знаменателей данных дробей. Выгодно выбирать общий знаменатель, возможно более низкой степени. Для того чтобы показать, как следует находить общий знаменатель, рассмотрим несколько примеров.

Пример:

Сложить дроби

Решение:

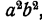
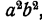
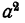
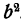
Сперва нужно привести эти дроби к общему знаменателю. В качестве общего знаменателя здесь можно взять так как делится на , на аb и на .

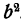
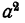
Для того чтобы привести дроби к общему знаменателю, умножим, числитель и знаменатель первой дроби на , второй — на ab, третьей— на . Получим

Можно принять за общий знаменатель и произведение
знаменателей данных дробей: 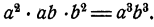При таком выборе общего знаменателя мы получим

Здесь возможно сокращение дробей. Действительно,

Таким образом, неэкономный выбор общего знаменателя приводит к появлению общих, множителей в числителе и знаменателе дроби,
получающейся в результате. Хотя их в конце концов можно сократить, но это удлиняет и усложняет выкладки.

Пример:

Выполнить сложение и вычитание

Решение:

Здесь за общий знаменатель следует принять 12 аbс. Числитель и знаменатель первой дроби нужно умножить на 4а, второй дроби — на Зb и третьей дроби — на 2с. Получим

Пример:

Выполнить сложение и вычитание

Решение:

Здесь мы можем заметить, что 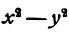= (x—у)(х + у). Поэтому за общий знаменатель мы можем принять (х—у)(х + у) Приняв это во внимание, проводим выкладки

Ответ.

Таким образом, если знаменателями слагаемых дробей
являются многочлены, то для целесообразного выбора общего знаменателя нужно предварительно разложить эти многочлены на множители, если, это возможно. За общий знаменатель нужно взять произведение всех полученных множителей, взятых в наибольшей степени, в которой они входят в знаменатели данных дробей.

Для каждой дроби нужно найти дополнительный множитель, на который нужно умножить числитель и знаменатель данной дроби, чтобы получить дробь со знаменателем, равным выбранному общему знаменателю.

Пример:

Выполнить сложение и вычитание

Решение:

Здесь за общий знаменатель следует принять

Пример:

Выполнить сложение и вычитание

Решение:

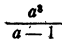
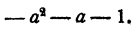
Здесь требуется сложить дробь c многочленом Для приведения к общему знаменателю умножим и раз делим многочлен на a—1. Получим

Умножение алгебраических дробей

При умножении алгебраических дробей применяется то же правило, что и при умножений численных дробей. Именно, произведение двух дробей равно дроби, числитель которой равен произведению числителей перемножаемых дробей, а знаменатель равен произведению знаменателей, т. е.

Здесь А, В, С, D обозначают любые алгебраические выражения.

В применении к обыкновенным численным дробям, т. е. в случае, если A, B, С, D — целые положительные числа, это правило известно из арифметики. В общем виде справедливость этого правила нуждается в доказательстве, так как значениями выражений A, В, С, D могут быть не только целые числа, но и дробные, не только положительные, но и отрицательные.

Проведем доказательство правила. Обозначим 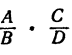буквой х и составим произведение

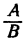
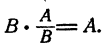
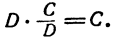
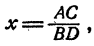
По определению действия деления есть число, которое при умножении на В дает A. Следовательно, Таким же образом Итак, BDx = А С. Отсюда заключаем, в силу определения действия деления, что что и требовалось доказать.

Пример:

Деление алгебраических дробей

Правило. Частное от деления двух дробей равно дроби,
числитель которой равен произведению числителя делимого на знаменатель делителя, а знаменатель равен произведению знаменателя делимого на числитель делителя, т. е.

Это правило иначе формулируется так: частное от деления двух дробей равно произведению делимого на дробь, числитель которой равен знаменателю делителя, а знаменатель равен числителю делителя.

Доказательство правила проводится посредством проверки деления умножением. Имеем:

что и требовалось доказать.

Пример:

Упрощение дроби, числитель и знаменатель которой являются алгебраическими суммами дробей

Пример:

Решение:

Здесь можно выполнить сложение дробей в числителе и знаменателе и затем поделить полученные результаты:

Однако проще непосредственно воспользоваться основным свойством дроби, именно умножить числитель и знаменатель на ab:

Для упрощения дроби, числитель и знаменатель которой являются алгебраическими суммами дробей, следует умножить числитель и знаменатель на общее кратное знаменателей всех дробей, находящихся в числителе и знаменателе.

Пример:

Решение:

Умножаем числитель и знаменатель на 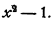Получим

Общие выводы

В § 12—14 мы убедились в том, что сумму, разность,
произведение и частное двух алгебраических дробей можно снова представить в виде алгебраической дроби или, в отдельных частных случаях, в виде многочлена. Отсюда следует, что любое дробное алгебраическое выражение может быть преобразовано к виду алгебраической дроби (или многочлена). Действительно, всякое дробное алгебраическое выражение есть запись результата действий сложения, вычитания, умножения и деления над числами и буквами. В результате первых по порядку действий сложения, вычитания и умножения мы придем к многочленам. В результате первого деления мы получим алгебраическую дробь. Результаты дальнейших действий над алгебраическими дробями будут представлять собой алгебраические дрцби, и окончательный результат также будет алгебраической дробью. При этом возможно, что многочлен, находящийся в числителе дроби, поделится на многочлен, находящийся в знаменателе, и тогда окончательный результат преобразуется к виду многочлена.

Пример:

Как уже говорилось в гл. III, цепочка тождественных преобразований алгебраического выражения называется алгебраической выкладкой.

В результате изложенного в гд. III, IV, V мы видим, что
алгебраическая выкладка может вестись в различных направлениях. При преобразовании целых алгебраических выражений можно раскрывать скобки, можно, наоборот, производить вынесение за скобку, при выполнении сложения многочлена и дроби можно сумму представить в виде одной дроби, а иногда бывает полезно выделение из данной дроби целой части, что приводит к разложению данной дроби на сумму многочлена и дроби и т, д.

Само собой разумеется, что алгебраическая выкладка должна? проводиться верно. Но этого недостаточно для полного овладения искусством алгебраической выкладки. Приведем один очень грубый пример:

Выкладка проведена верно, но бессмысленность ее бросается в глаза, Зачем было производить какие-то преобразования, чтобы вернуться к исходному выражению?

Алгебраическая выкладка всегда должна быть направлена к определенной цели. В упражнениях цель бывает обычно указана в условии, например «разложить на множители», «сложить дроби» и т, д.
Часто целью является упрощение данного алгебраического выражения. Но в применениях алгебры к решению практических задач нужно уметь найти цель в проведении выкладки.

Пример:

При решении некоторой задачи в общем виде ответ получен в виде формулы 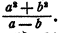Требуется вычислить х с тoчностью до 0,1 при а=51, 52, 53, 54, 55 и при b = 3, 4, 5,

Решение:

Здесь целесообразно сделать следующее
преобразование:

По внешнему виду мы даже несколько усложнили ответ, но считать после преобразования становится много легче, так как мы избавились от необходимости возводить большое число а в квадрат, а затем делить большое число 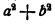на a — b. Например, при a = 51, b = 3 по исходной формуле

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник