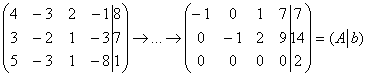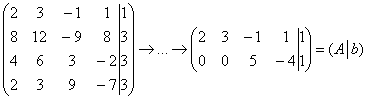Совместность системы как проверить
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Способ №1. Вычисление рангов по определению.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Система \(m\) линейных алгебраических уравнений с \(n\) неизвестными (сокращенно СЛАУ) представляет собой систему вида
\( \left\< \begin
СЛАУ называют однородной, если \( b_1 = b_2 = \ldots = b_m = 0 \). Иначе её называют неоднородной.
Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.
Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При \(m=n\), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
Формы записи СЛАУ
Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.
Таким образом, решение СЛАУ (1) можно трактовать как представление столбца \(b\) в виде линейной комбинации столбцов \( a_1, \ldots, a_n \). Соотношение (2) называют векторной записью СЛАУ.
Поскольку \(A \;,\; X\) и \(B\) являются матрицами, то запись СЛАУ (1) в виде \(AX=B\) называют матричной. Если \(B=0\), то СЛАУ является однородной и в матричной записи имеет вид \(AX=0\).
Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида \(AX=B\)
являются просто различной формой записи одной и той же задачи.
Критерий совместности СЛАУ
«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
Матрицу
\( A = \begin
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
\( (A|B) = \left( \begin
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Теорема Кронекера-Капелли. Для совместности СЛАУ \(AX=B\) необходимо и достаточно, чтобы ранг её матрицы \(A\) был равен рангу её расширенной матрицы \( (A|B) \).
Формулы Крамера
Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = \frac<\Delta_i> <|A|>\;,\quad i=\overline <1,n>\tag <3>$$
где \(\Delta_i\) — определитель матрицы, получающейся из матрицы \(A\) заменой \(i\)-го столбца на столбец свободных членов.
Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.
Однородные системы
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
Определение. Любой набор из \(k=n-r\) линейно независимых столбцов, являющихся решениями однородной СЛАУ \(AX=0\), где \(n\) — количество неизвестных в системе, а \(r\) — ранг её матрицы \(A\), называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице \(A\) однородной СЛАУ \(AX=0\) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.
Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.
Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ <(1)>+ \ldots + c_kX^ <(k)>$$
где постоянные \( c_i \;, \quad i=\overline <1,k>\), принимают произвольные значения.
Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.
Неоднородные системы
Рассмотрим произвольную СЛАУ \(AX=B\). Заменив столбец \(B\) свободных членов нулевым, получим однородную СЛАУ \(AX=0\), соответствующую неоднородной СЛАУ \(AX=B\). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема. Пусть столбец \(X^\circ\) — некоторое решение СЛАУ \(AX=B\). Произвольный столбец \(X\) является решением этой СЛАУ тогда и только тогда, когда он имеет представление \(X = X^\circ + Y \), где \(Y\) — решение соответствующей однородной СЛАУ \(AY=0\).
Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение \(X^\circ\) этой системы, чтобы свести её к однородной системе.
Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.
Ранги этих матриц связаны неравенством 
Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.
Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть 
В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:
1) отыскать в матрице системы A ранга 

2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор 
3) члены с коэффициентами, не входящими в 

Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
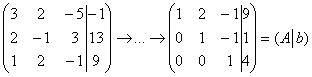
Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор
отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному 

Оставшиеся неизвестные определяются из системы
Решая последнюю систему по формулам Крамера или иным способом, находим



Присоединяя сюда 
Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы:

Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:

Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:
Решая последнюю систему по формулам Крамера, находим



Как исследовать систему линейных уравнений на совместность?
Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли, которую я сформулирую в необходимом виде:
Если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.
Таким образом, для исследования системы на совместность нужно проверить равенство 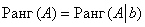
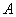
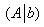
Исследовать систему на совместность и найти её решение, если система совместна
А когда системы уже прорешаны – просто вдвойне… нет – втройне =)
Решение: тем не менее, обратим внимание на строгую верхнюю строчку – по условию,
в первую очередь, требуется проверить систему на совместность. Как начать решение?
В любом случае записываем расширенную матрицу системы и с помощью элементарных преобразований приводим её к ступенчатому виду:
а) Пример №1 статьи о методе исключения неизвестных:
Элементарные преобразования не меняют ранга матриц, поэтому в результате выполненных действий получены эквивалентные исходным матрица системы 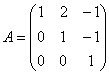
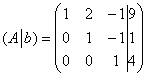
Максимальный порядок ненулевого минора матрицы системы равен трём. Здесь таковой минор в единственном экземпляре и совпадает он, понятно, с определителем самой матрицы:
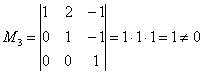
Следовательно, 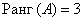
Максимальный порядок ненулевого минора расширенной матрицы системы также равен трём:
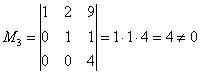
Таким образом, 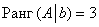
Вывод: 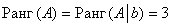
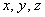
Что дальше? Дальше следует непосредственно решить систему. Если по условию не предложен способ, то, конечно же, раскручиваем обратный ход метода Гаусса. Если требуется решить систему методом Крамера или с помощью обратной матрицы, ну что поделать….
б) Пример №1 статьи о несовместных системах и системах с общим решением:
В результате элементарных преобразований получена эквивалентная матрица системы 
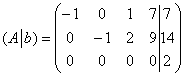
Максимальный порядок ненулевого минора матрицы системы равен двум, например:
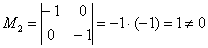
Заметьте, что здесь есть возможность выбрать и другой минор 2-го порядка, но проще всего в качестве примера взять ступенчатый определитель.
Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например:
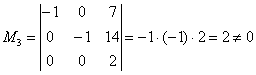
Таким образом, 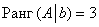
Вывод: 
Однако помните – если по условию не требуется исследовать систему на совместность, то вполне достаточно ограничиться стандартным ответом (см. решение вышеуказанного урока).
в) Пример №3 той же статьи:
В результате элементарных преобразований получена эквивалентная матрица системы 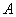
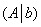
Максимальный порядок ненулевого минора матрицы системы равен двум, например:
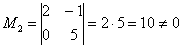
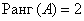
Максимальный порядок ненулевого минора расширенной матрицы системы также равен двум, например:
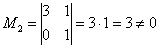
Второй абзац можно полностью заменить хитрой лаконичной фразой: «по этой же причине 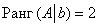
Вывод: 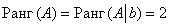
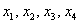
Далее находим общее решение по стандартной схеме.
Образец исследования системы на совместность также можно посмотреть в начале
Примера №1 урока о нахождении различных базисных решений системы.
…Всё-таки иногда удивительно обманываются ожидания – порой думаешь, что статья получится огромной, а она оказывается весьма компактной, а иногда, как сейчас – наоборот. Посмотрел статистику и жутко удивился добрым 20-ти тысячам символов. Поэтому всем высокого ранга и до скорых встреч!
Пример 2: Решение: поскольку в матрице есть ненулевые элементы, то её ранг не меньше единице.
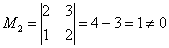
Рассмотрим миноры 3-го порядка, при этом в них обязательно должен содержаться ненулевой минор 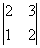
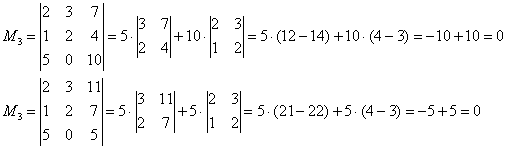
Максимальный порядок ненулевого минора равен двум.
Ответ:
Пример 4: Решение: с помощью элементарных преобразований приведем матрицу к ступенчатому виду:
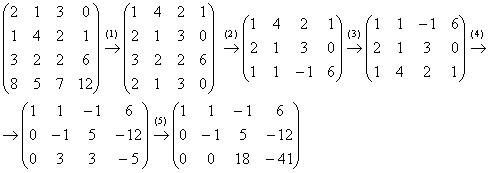
(1) Первую и вторую строки поменяли местами. К 4-ой строке прибавили 3-ю строку, умноженную на –2.
(2) Вторая и 4-ая строки одинаковы, 4-ю строку удалили. К третьей строке прибавили вторую строку, умноженную на –1.
(3) Первую и третью строки поменяли местами.
(4) Ко второй строке прибавили первую строку, умноженную на –2. К 3-ей строке прибавили первую строку, умноженную на –1.
(5) К третьей строке прибавили вторую строку, умноженную на 3.
В результате получены 3 строки, значит, ранг матрицы равен 3.
Ответ:
Пример 6: Решение: ранг матрицы не превосходит минимальной размерности, то есть, трёх.
В матрице есть ненулевые элементы, значит, ранг не менее единицы.

Максимальный порядок ненулевого минора равен трём
Ответ:
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?