Спираль архимеда как сделать
Спираль архимеда как сделать
Стороны квадратов в «золотом прямоугольнике» равны соответственно числам Фибоначчи 1 1 2 3
Стороны квадратов в «золотом треугольнике» равны соответственно числам Фибоначчи 1 1 2 3 5 8 13
Леонардо Пизанский (Leonardo Pisano), Фибоначчи (Fibonacci) — итальянский математик (1180-1240). Родился в Пизе. Он долгое время жил на Востоке, где познакомился с математикой арабов. Достижения арабских математиков Фибоначчи продвигал в Западную Европу:
· В 1202 г. Леонардо написал труд под названием «Книга абака» (Liber Abaci). «Книга абака» стала первой математической энциклопедией средневековья, сыгравшей существенную роль в развитии математики в Европе.
· Самым главным трудом Леонардо считается Liber Abaci (1202).
В «Книге абака» Леонардо сформулировал задачу о кроликах:
«Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару? «
· В 1220 г. Фибоначчи издал сочинение: «Практика геометрии» (Practica geometria).
Фибоначчи решил множество сложных математических и практических проблем, опередив на столетия развитие науки. Е го идеи легли в основу огромного множества исследований, которыми занимается современная математическая наука.
Фибоначчи занимался проблемами торговли и решал практические задачи, например: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказал, что оптимальной является такая система гирь: 1, 2, 4, 8, 16.
Как начертить правильную спираль
Спиралью называется плоская кривая, описываемая точкой, удаляющейся от центра при совершении кругового движения в плоскости чертежа вокруг центра спирали. На практике различают спирали с постоянным и постепенно возрастающим расстоянием между завитками. Обычно спирали строят по точкам и вычерчивают с помощью лекала.
Для того чтобы расчертить спираль, необходимо наметить не менее двух ее центров. Если вычерчивают спираль из трех или более центров, то обычно центрами спирали являются вершины правильного треугольника или правильного многоугольника. Каждую дугу проводят из последующей вершины до пересечения с лучом из угла треугольника или многоугольника. Радиус при этом каждый раз увеличивается на длину, равную длине стороны треугольника или многоугольника.
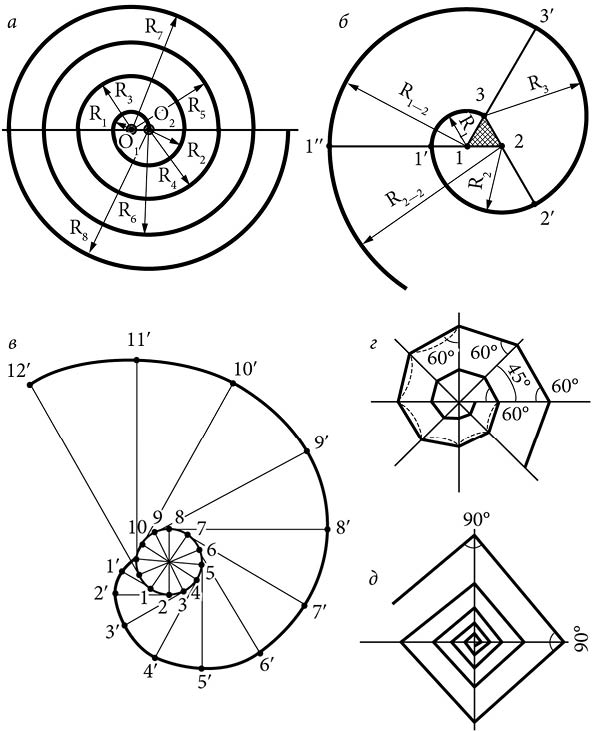
Рассмотрим, например, как начертить так называемую «архимедову спираль» (рис. 17, а ). Для этого нужно провести горизонтальную линию и отметить на ней две точки О 1 и О 2, отстоящие одна от другой примерно на 3 мм. Поставив ножку циркуля в одну из этих точек (О 1), проведите дугу радиусом 3 мм (R 1), равную половине окружности. Концы этой дуги должны опираться на горизонтальную ось (в данном примере – сверху).
Для построения спирали, имеющей три центра (рис. 17, б), находящихся на равных расстояниях один от другого, необходимо предварительно построить равносторонний треугольник 1–2–3 (заштрихован) и продолжить его стороны так, как это показано на рисунке (линии 1–1’, 2–2’ и 3–3’ ).
Рис. 17. Построение спиралей: а – «архимедова спираль» с двумя центрами; б – трехцентровая спираль; в – эвольвента круга; г, д – ломаные (хордовые) спирали.
Аналогично выполняют спирали с четырьмя, пятью и т. д. центрами.
Содержание
Формула [ править | править код ]
Уравнение для золотой спирали в полярной системе координат то же самое, что и для других логарифмических спиралей, но со специальным значением коэффициента роста – φ 4 :
r = a φ ± 2 θ π >> 
где a — произвольная положительная вещественная константа, а φ = 5 + 1 2 >+1> >> 
Основное свойство логарифмической спирали: угол между радиус-вектором, исходящим из полюса, и касательной к спирали – μ – постоянен, и для золотой спирали определяется формулой:
tg μ = r r ′ = π 2 ln φ mu = 

Откуда μ ≈ 73 ∘ > 
Приближения золотой спирали [ править | править код ]
Как уже было написано выше, при вписывании золотой спирали в последовательность вложенных друг в друга золотых прямоугольников, она аппроксимируется спиралью, построенной по методу Дюрера. Золотой прямоугольник можно разделить на квадрат и подобный ему прямоугольник, его, в свою очередь, разделить тем же образом, и продолжать этот процесс произвольное число раз. Если в эти квадраты вписать соединенные между собой четвертинки окружностей, то получается спираль, изображенная на первом рисунке.
Ещё одной аппроксимацией является спираль Фибоначчи, которая строится подобно вышеописанной спирали, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины. Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов (см. второй рисунок).
Спирали в природе [ править | править код ]
Построение спирали Архимеда.
Спираль Архимеда – это траектория точки, движущейся с постоянной скоростью от центра окружности по
радиусу, вращающемуся также с постоянной угловой скоростью.
1. Делим радиус окружности на одинаковое число равных частей (в примере на 8).
2. Делим окружность на такое же число равных частей.
3. Проводим лучи из центра через точки деления окружности.
4. На первом луче откладываем одно деление радиуса.
5. На втором луче откладываем два деления радиуса и т. д.
6. Если строить спираль дальше, то на луче 1 откладываем 8+1 деление радиуса (получаем точку IX ).
8. На третьем луче откладываем 8+3 деления радиуса (получаем точку XI) и т. д.
Соединяем точки по лекалу.
Спираль. Спираль Архимеда. Построение спирали Архимеда.
Как построить параметризированную геометрию спирали Архимеда
Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).
Что такое спираль Архимеда?
Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.
В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.
Уравнение спирали Архимеда в полярной системе координат записывается, как:
Задание параметризированной геометрии спирали Архимеда
Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.
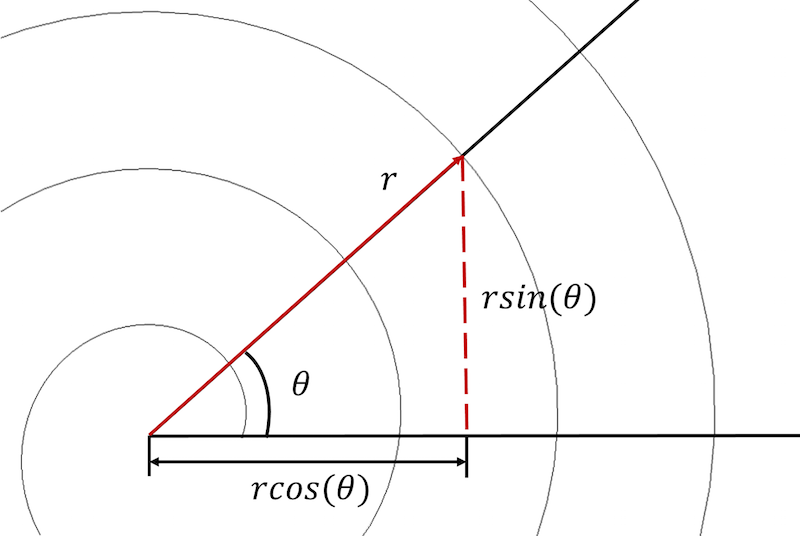
Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.
Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:
После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:
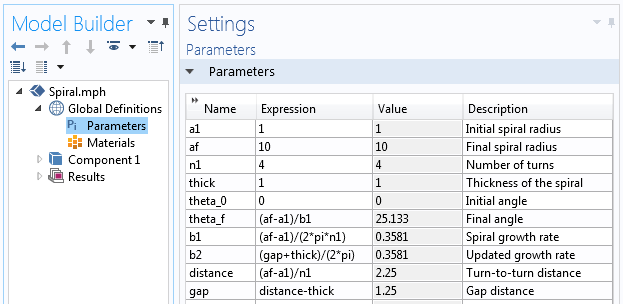
Параметры, которые используются для построения геометрии спирали.
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):
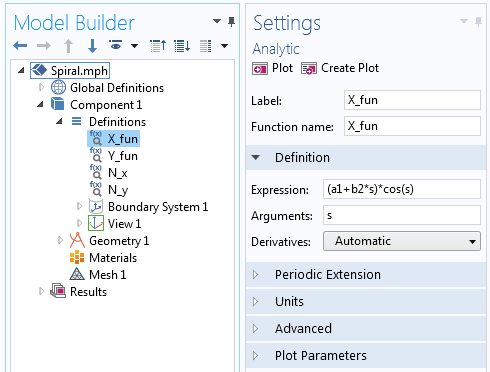
Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.
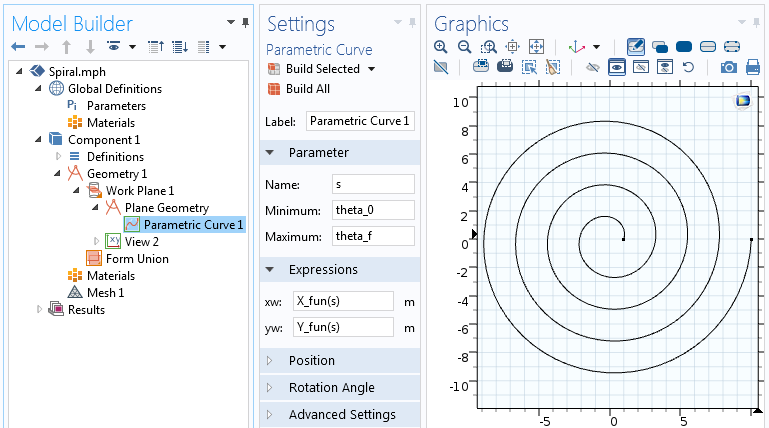
Настройки для Parametric Curve (Параметрической кривой).
Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.
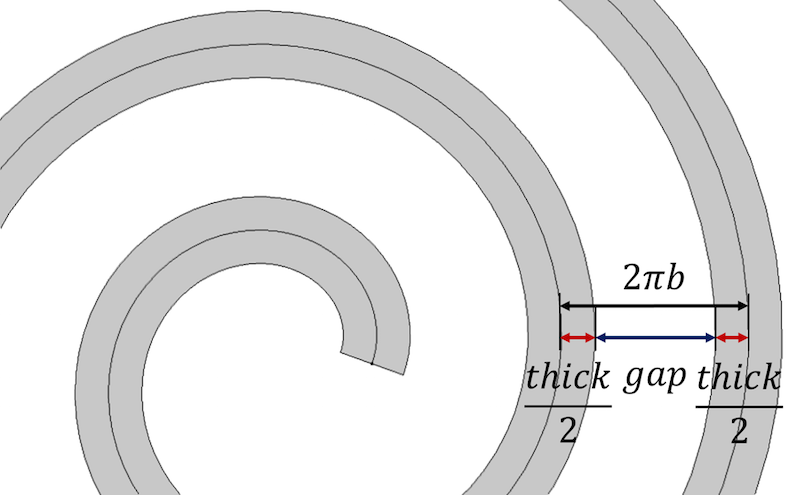
Расстояние между витками определяется толщиной спирали и величиной зазора.
Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:
После этого выражаем показатель роста спирали через толщину:
Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:
где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:
Обновленные параметрические уравнения спирали Архимеда со смещением:
Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:
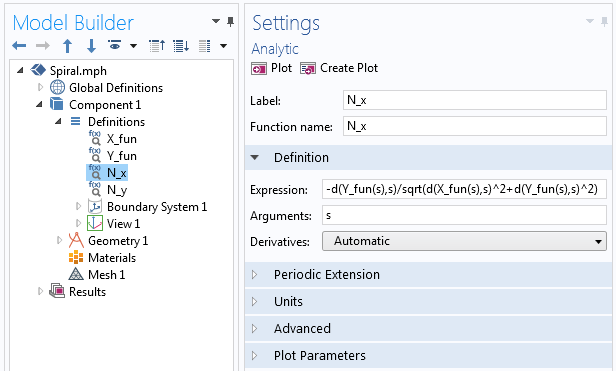
Примеры оператора производной, который используется в аналитической функции
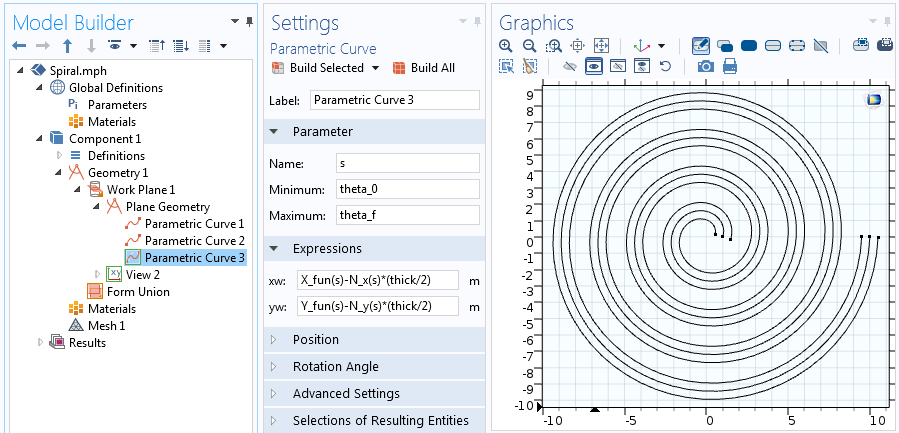
Выражения для второй смещённой параметрической кривой.
Уравнения кривой на конце:
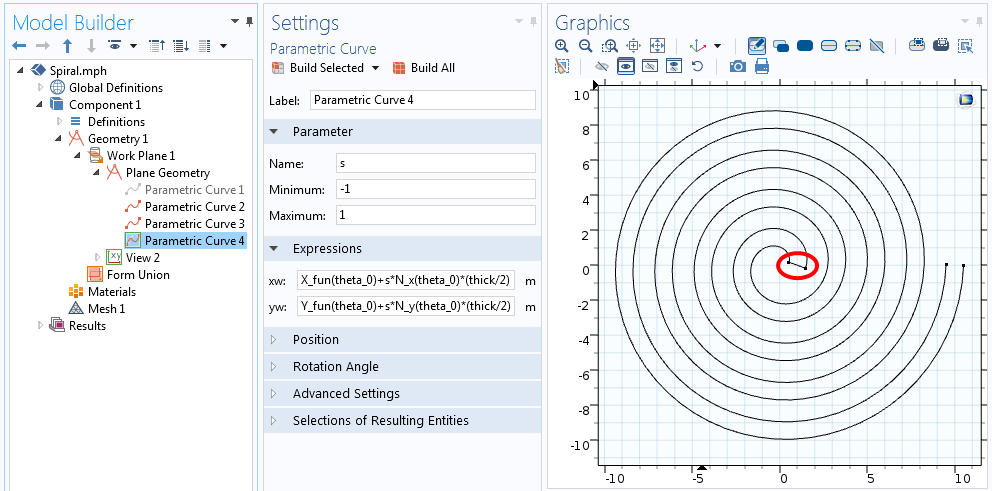
Уравнения кривой, соединяющей спираль в центре.
В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.
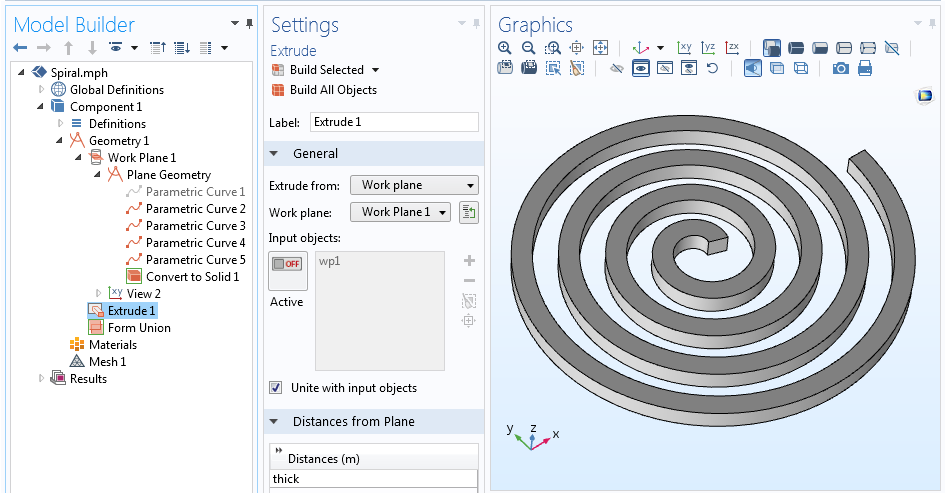
Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.
Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics
В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.
Как построить параметризированную геометрию спирали Архимеда
Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).
Что такое спираль Архимеда?
Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.
В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.
Уравнение спирали Архимеда в полярной системе координат записывается, как:
Задание параметризированной геометрии спирали Архимеда
Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.
Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:
После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

Параметры, которые используются для построения геометрии спирали.
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):

Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

Настройки для Parametric Curve (Параметрической кривой).
Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

Расстояние между витками определяется толщиной спирали и величиной зазора.
Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:
После этого выражаем показатель роста спирали через толщину:
Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:
где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:
Обновленные параметрические уравнения спирали Архимеда со смещением:
Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:

Примеры оператора производной, который используется в аналитической функции

Выражения для второй смещённой параметрической кривой.
Уравнения кривой на конце:

Уравнения кривой, соединяющей спираль в центре.
В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.
Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics
В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.
Построение спирали Архимеда
Эвольвенты также относятся к спиралям; они имеют две ветви в зависимости от направления развертывания кривой.
На практике используют и спирали, составленные из дуг окружностей (их называют завитками), проводимых из двух, трех и более центров, расположенных в вершинах правильных многоугольников (на рис. 3.9 из двух центров — О1 и O2).
На рис. 3.10 — пример использования четырехцентрового завитка в очертании центробежного вентилятора.
Синусоиду (рис. 3.11) строят по заданному диаметру начальной окружности. Выбирают начало координат, совпадающее с точкой А на окружности заданного радиуса R, и на продолжении оси ОА откладывают отрезок АА1 = 2πR (равный длине окружности). Делят окружность и отрезок AA1 на одинаковое число равных частей и пронумеровывают точки деления. Через точки деления окружности проводят ряд прямых, параллельных АА1; из точек деления прямой АА1 — ряд прямых, перпендикулярных AA1. На пересечении этих вспомогательных прямых, имеющих одноименные номера, отмечают точки синусоиды.
Вид синусоиды имеют многие кривые, изображающие гармонические колебательные процессы или являющиеся проекциями винтовых линий. Для их построения выполнение условия АА1 = 2πR не является обязательным, но принцип деления исходной окружности и прямой АА1 сохраняют.
Кривые 2-го порядка. Их свойства — геометрические, баллистические, оптические, акустические и др.— широко используют в самых разнообразных отраслях науки и техники.
Эллипс — множество точек плоскости, сумма расстояний (радиусов-векторов) каждой из которых до двух данных точек той же плоскости (фокусов. От лат. focus — огонь, очаг.) есть величина постоянная (равная 2R — большой оси эллипса).
Один из вариантов построения эллипса по большой (2R) и малой (2r) осям приведен на рис. 3.12. При построении проводят окружности радиусами r и R из одного центра О и произвольный радиус ОА. Из точек пересечения 1 и 2 проводят прямые, параллельные осям эллипса, и в точке их пересечения отмечают точку М эллипса. Аналогично строят необходимое число точек.
Построение осей эллипса по заданным его сопряженным диаметрам. Поворачивают один из сопряженных полудиаметров на 90° (рис. 3.13). Полученную точку H1 соединяют с точкой E и из точки O1 делящей отрезок Н1Е пополам, проводят дугу радиуса OO1. Точки L и K определят направлений осей, а их величины — отрезки KH1 и H1L. Построение не изменится, если использовать острый угол между сопряженными полудиаметрами.