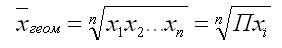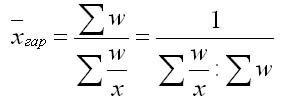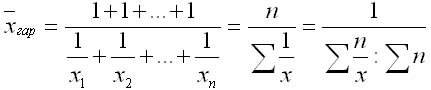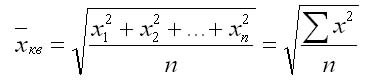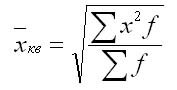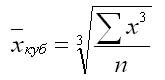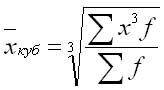Средняя геометрическая вычисляется как

Среднее геометрическое чисел

В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.

Расчет среднего геометрического

Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.

Частные случаи формулы:

» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Количество чисел	Формула
2	» data-order=»«>
3	» data-order=»«>
4	» data-order=»«>

Пример задачи

Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.

Решение:
Воспользуемся соответствующей формулой для трех чисел:

Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.

Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. ):

Источник

Среднее геометрическое чисел – формула и примеры

Средние величины в статистике дают обобщающую характеристику анализируемого явления. Самая распространенная из них – среднее арифметическое. Она применяется, когда агрегатный показатель образуется с помощью суммы элементов. Например, масса нескольких яблок, суммарная выручка за каждый день продаж и т.д. Но так бывает не всегда. Иногда агрегатный показатель образуется не в результате суммирования, а в результате умножения.

Такой пример. Месячная инфляция – это изменение уровня цен одного месяца по сравнению с предыдущим. Если известны показатели инфляции за каждый месяц, то как получить годовое значение? С точки зрения статистики – это цепной индекс, поэтому правильный ответ: с помощью перемножения месячных показателей инфляции. То есть общий показатель инфляции – это не сумма, а произведение. А как теперь узнать среднюю инфляцию за месяц, если имеется годовое значение? Нет, не разделить на 12, а извлечь корень 12-й степени (степень зависит от количества множителей). В общем случае среднее геометрическое рассчитывается по формуле:

То есть корень из произведения исходных данных, где степень определяется количеством множителей. Например, среднее геометрическое двух чисел – это квадратный корень из их произведения

Среднее геометрическое трех чисел – кубический корень из произведения

и т.д.

Если каждое исходное число заменить на их среднее геометрическое, то произведение даст тот же результат.

Чтобы лучше разобраться, чем отличаются среднее арифметическое и среднее геометрическое, рассмотрим следующий рисунок. Имеется прямоугольный треугольник, вписанный в круг.

Из прямого угла опущена медиана a (на середину гипотенузы). Также из прямого угла опущена высота b, которая в точке P делит гипотенузу на две части m и n. Т.к. гипотенуза – это диаметр описанного круга, а медиана – радиус, то очевидно, что длина медианы a – это среднее арифметическое из m и n.

Рассчитаем, чему равна высота b. В силу подобия треугольников АВP и BCP справедливо равенство

Значит, высота прямоугольного треугольника – это среднее геометрическое из отрезков, на которые она разбивает гипотенузу. Такое наглядное отличие.

В MS Excel среднюю геометрическую можно найти с помощью функции СРГЕОМ.

Все очень просто: вызвали функцию, указали диапазон и готово.

На практике этот показатель используют не так часто, как среднее арифметическое, но все же встречается. Например, есть такой индекс развития человеческого потенциала, с помощью которого сравнивают уровень жизни в разных странах. Он рассчитывается, как среднее геометрическое из нескольких индексов.

Ниже видео, как найти среднее геометрическое чисел в Excel.

Источник

Среднее геометрическое

Предлагаемая здесь программа, помимо расчета среднего геометрического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.

Среднее геометрическое или среднее пропорциональное используется человечеством в архитектурных, землемерных и инженерных расчетах не менее 2500 лет. Об этом достоверно известно благодаря математическому трактату Евклида «Начала».
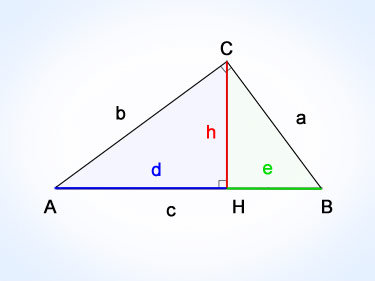
В своей второй теореме Евклид доказывает, что в прямоугольном треугольнике высота проведенная из прямого угла (рисунок) делит противоположную сторону так что:

Собственно говоря, благодаря второй теореме Евклида среднее геометрическое и получило свое название. В древнем мире математики ограничивалось только использованием корня квадратного (геометрия) и корня кубического (стереометрия).
Вообще говоря, извлечение корня с различными целыми показателями является частным случаем дробной степени. Но к такому пониманию этих алгебраических операции математики подошли только в семнадцатом веке. Неоценимый вклад в достижении обобщенного понимания степенных алгебраических операции внес Рене Декарт.

В свете современных представлений:

Среднее геометрическое значение множества положительных вещественных чисел определяется как результат взаимного умножения этих чисел и извлечения из произведения корня с показателем равным количеству чисел:

Таким образом, мы имеем дело исключительно с положительными вещественными числами и находим такое число, что при замене каждого из этих чисел их произведение не изменяется.

Расчет среднего геометрического

Введите исходные данные

Что-то пошло не так. Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°

Среднее геометрическое, a_{ср. геом}

Для наглядной демонстрации правила о средних

выводим так же результат расчета среднего арифметического:

Среднее арифметическое [1] , a_{ср. арифм}

Design by Sergey Ov for abc2home.ru

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего геометрического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа, цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый, и автоматически начнется расчет среднего геометрического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Страницы по теме «Расчет средних значений»

Свойства среднего геометрического

1. Среднее геометрическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.

2. Кроме того среднее геометрическое подчиняется неравенству о средних для множества положительных вещественных чисел

то есть для любого множества положительных чисел среднее геометрическое никогда не бывает больше среднего арифметического [1] :

Прикладное значение среднего геометрического

P.S. На этой странице используется Бета версия программы расчета среднего геометрического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Среднее арифметическое значение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

2. Среднее степенное значение s_d порядка (степени) d от множества заданных чисел a ₁ + a ₂ + …+ a _n определяется формулой:

Источник

Средняя геометрическая в статистике

Понятие средней геометрической

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.

В контрольных по статистике она исчисляется извлечением корня степени n из произведений отдельных значений — вариантов признака Х по формуле:

где П — оператор умножения, знак произведения;
n — число вариантов.

Средняя геометрическая в частности рассчитывается тогда, когда данные даны в процентах.

Рассчитаем среднюю величину инфляции

Исходные данные взяты из справочника «Краткосрочные экономические показатели Российской Федерации за 2012 г.». Сайт www.gks.ru

год	квартал	Индекс потребительских цен, y
2008	1	104,8
	2	103,8
	3	101,7
	4	102,5
2009	1	105,4
	2	101,9
	3	100,6
	4	100,7
2010	1	103,2
	2	101,2
	3	101,8
	4	102,4
2011	1	103,8
	2	101,1
	3	99,7
	4	101,4

Среднемесячный индекс потребительских цен определяется по формуле средней геометрической, т.к. в основе расчета лежит индекс. Перемножим данные и разделим на число кварталов за 4 года:

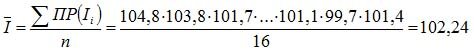
Вывод: в период с 2008 по 2011 года средний квартальный прирост инфляции составил 2,24%

Средняя гармоническая

Определяющее свойство средней гармонической заключается в том, чтобы при осреднении оставалась неизменной сумма величин, обратных осредняемым.

Формула средней геометрической взвешенной применяется в тех случаях, когда статистическая информация не содержит частот f по отдельным вариантам х совокупности и представлена как их произведение xf. Для того чтобы исчислить среднюю геометрическую, необходимо обозначить: xf = w, откуда f = w/x.

Преобразуем формулу средней арифметической так, чтобы по имеющимся данным х и w можно было вычислить среднюю. В формулу средней арифметической взвешенной вместо xn подставим w, а вместо n — отношение w/x и таким образом получим формулу средней гармонической взвешенной:

Средняя гармоническая простая применяется в тогда, когда вес каждого варианта равен единице. Она вычисляется по формуле:

где 1/x — отдельные варианты обратного признака, встречающиеся по одному разу;

n — число вариантов.

Средняя квадратичная

Средняя квадратичная применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.

Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.

Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

Средняя квадратичная взвешенная вычисляется по формуле:

где f — признак веса.

Средняя кубическая

Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:

Средняя кубическая взвешенная:

Средняя квадратическая и средняя кубическая имеют неширокое применение в практической статистике. Часто в статистике используют среднюю квадратическую, но не из самих факторов х, и из их отклонений от средней при расчете показателей вариации.

Средняя может быть рассчитана не для всей, а для какой-либо части данных совокупности. Примером может быть средняя прогрессивная как одна из частных средних, рассчитанная не для всех, а только для «лучших» (например, для показателей выше или ниже средних индивидуальных).

Структурные средние

Для характеристики центральной тенденции в статистических распределениях рационально вместе со средней арифметической использовать некое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.

Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.

Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних.
Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода и медиана очень часто рассчитывают в задачах статистики и они являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа типа рядов распределения, которое может нормальным, асимметричным, симметричным и т.д.

Также как и медиану вычисляются значения признака, делящего совокупность на четыре равные части — квартели, на пять частей — квинтели, на десять равных частей — децели, на сто равных частей — перцентели. Использование при анализе вариационных рядов распределения рассмотренных характеристик в статистике позволяет более глубоко и детально охарактеризовать изучаемую совокупность.

Источник

Когда применять среднее геометрическое: ключевые примеры

Что такое среднее геометрическое?

В статистике среднее геометрическое вычисляется путем возведения произведения ряда чисел до значения, обратного общей длине ряда. Среднее геометрическое наиболее полезно, когда числа в серии не независимы друг от друга или если числа имеют тенденцию к большим колебаниям.

Применение среднего геометрического наиболее распространено в бизнесе и финансах, где оно часто используется при работе с процентами для расчета темпов роста и доходности портфеля ценных бумаг.Он также используется в некоторых индексах финансовых и фондовых рынков, таких какгеометрический индекс линии ценностиFinancial Times.

Понимание среднего геометрического

Темпы роста

Среднее геометрическое используется в финансах для расчета средних темпов роста и называется совокупным годовым темпом роста. Рассмотрим акции, которые вырастают на 10% в первый год, падают на 20% во второй год, а затем вырастают на 30% в третий год. Среднее геометрическое значение скорости роста рассчитывается следующим образом:

В доходности портфеля

Среднее геометрическое обычно используется для расчета годовой доходности портфеля ценных бумаг. Рассмотрим портфель акций, который вырастает со 100 до 110 долларов в первый год, затем снижается до 80 долларов во второй год и поднимается до 150 долларов в третий год. Затем доходность портфеля рассчитывается как (150 долл. США / 100 долл. США) ^ (1/3) = 0,1447 или 14,47%.

В фондовых индексах

Среднее геометрическое также иногда используется при построении фондовых индексов.Многие из индексов Value Line, публикуемыхFinancial Times, используют среднее геометрическое.  В этом типе индекса все акции имеют равный вес, независимо от их рыночной капитализации или цен. Индекс рассчитывается путем взятия среднего геометрического пропорционального изменения цены каждой акции в составе индекса.

Корни в геометрии

Среднее геометрическое было впервые концептуализировано греческим философом Пифагором Самосским и тесно связано с двумя другими классическими средствами, прославившимися им: средним арифметическим и средним гармоническим.

Среднее геометрическое также используется для наборов чисел, где значения, умноженные вместе, являются экспоненциальными. Примеры этого явления включают процентные ставки, которые могут быть привязаны к любым финансовым инвестициям, или статистические ставки при росте населения.

Источник