Степенная башня как считать

Тетрация

Тетрация (гипероператор-4) в математике — итерационная функция экспоненты, следующий гипероператор после возведения в степень. Тетрация используется для описания больших чисел.

Содержание

Определения

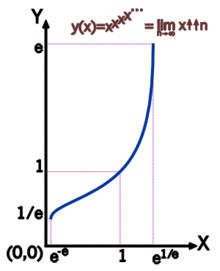
Тетрация как степенная башня

Для любого положительного вещественного числа 0″ border=»0″ /> и неотрицательного целого числа , тетрацию можно определить рекуррентно:

Согласно данному определению, вычисление тетрации, записанной как «степенная башня», возведение в степень начинается с самых дальних уровней к начальному (в данной системе обозначений, с самого наивысшего показателя степени):

При этом, так как возведение в степень не является ассоциативной операцией, то вычисление выражения в другом порядке приведёт к другому ответу:

Таким образом, степенные башни должны вычисляться сверху-вниз (или справа-налево), то есть, иначе говоря, они обладают правой ассоциативностью.

Тетрация как гипероператор

Тетрация является четвёртой по счёту гипероперацией:

Здесь каждая операция является итерацией предыдущей.

Свойства

Терминология

Существует несколько терминов для определения понятия тетрация и за каждым из них стоит своя логика, но некоторые из них не стали общепринятыми в силу тех или иных причин. Ниже приведено несколько подобных примеров.

Тетрацию также часто путают с другими тесно связанными функциями и выражениями. Ниже приведено несколько связанных терминов:

Форма	Терминология
	Тетрация
	Итерационные экспоненты
	Вложенные экспоненты (также башни)
	Бесконечные экспоненты (также башни)

В первых двух выражениях есть основание, и количество появляющихся есть высота. В третьем выражении, есть высота, но все основания разные.

Обозначения

Системы записи в которых тетрация может быть использована (некоторые из них позволяют использование даже более высоких итераций) включают в себя:

Имя	Форма	Описание
Стандартная форма записи		Использована Мауером (Maurer) [1901] и Гудштейном [1947]; популяризовано в книге Руди Рюкера «Infinity and the Mind».
Стрелочная нотация Кнута		Позволяет удлинение путём добавление добавочных или индексированных стрелочек, является более мощным способом.
Цепочка Конвея		Позволяет удлинение путём прибавления 2 (эквивалентно вышеописанному способу), но также возможно даже более мощный способ записи, если увеличивать цепочку
Функция Аккермана		Допускает особый случай в записи в терминах функции Аккермана.
Итерируемая экспоненциальная форма записи		Позволяет простое удлинение до итерационных экспонент начиная со значений отличных от 1.
Обозначения Хусменд (англ. Hooshmand ) [6]
Система записи гипероператорами		Позволяет удлинение путём прибавления 4; это даёт семейство гипероператоров.
Система записи ASCII	a^^n	Так как запись стрелочка наверх используется идентично обозначению корректурного знак вставки ( ^ ), оператор тетрация может быть записан в виде ( ^^ ).
Нотация массивов Бауэрса		= a^^^. ^^^b (c стрелок сверхстепени).

Одна из вышеприведённых систем использует систему записи итерированных экспонент; в общем случае это определяется следующим образом:

Не так много обозначений существует для итерированных экспонент, но несколько из них показаны ниже:

Имя	Форма	Описание
Стандартная форма записи		Система записи и итерационная система записи была введена Эйлером.
Стрелочная нотация Кнута		Позволяет для суперстепеней и суперэкспоненциальных функций увеличивать число стрелочек.
Гипер-Е нотация	E(a)x#n
Система записи Иоанна Галидакиса (англ. Ioannis Galidakis )		Допускает использование больших выражений в основании. [7]
ASCII (добавочный)	a^^n@x	Основана на взгляде, что итерационная экспонента есть добавочная тетрация.
ASCII (стандартный)	exp_a^n(x)	Основана на стандартной форме записи.

Примеры

В нижеприведённой таблице большинство значений слишком огромны, чтобы их записать в экспоненциальном представлении, по этой причине используется система записи в виде итерационных экспонент, чтобы представить их с основанием 10. Значения, содержащие десятичную запятую, являются приблизительными.

Источник

nagato

Перезагрузка

Одобрено министерством культуры [16+]

В прошлый раз досчитали до порядков гуголплекса — наибольших чисел, которые как бы можно записать в десятичной нотации. Да, нам потребуется нанокарандаш и вся Вселенная, но, теоретически хотя бы можно представить, как бы мы его записывали. Но на этом счёт не заканчивается, и за гуголплексами, гугоплексами в степени гуголплекс и факториалами всего этого добра, живут такие чудища, которые невозможно ни представить, ни понять. При этом, эти чудища являются решениями вполне себе определённых задач и имеют практический смысл.

Вводная
На определённом этапе у нас закончатся возможности для записи чисел. Сначала мы будем использовать десятичную нотацию, потом сложение и мультипликацию, потом записывать числа в виде степеней, потом в виде степенных башен. Но для чисел, о которых пойдёт речь далее нам уже не хватит Вселенной (и мультивселенной тоже), чтобы записать степенную башню так, если бы размер каждой цифры был планковским!

Смотрите, функция растёт очень быстро, при изменении одного из аргументов «всего лишь на единичку», мы уже вышли за гуголплекс, но это только начало.

3 ↑↑↑ 4 — эта хрень относится уже к наглым издевательствам над здравым смыслом. Если раньше можно было ещё хоть как-нибудь пытаться представить, как выглядела бы степенная башня из троек до Марса и сделать вид, что такое число можно осознать, то тут — всё. Нескольких Вселенных уже будет недостаточно, чтобы организовать башню высотой из 7 625 597 484 987 башен до Марса. Но, всё же, пока мы ещё оперируем хоть какими-то категориями. Дальше они заканчиваются, потому что.

А дальше, как несложно догадаться будет a ↑↑↑↑↑ b или a ↑ 5 b и так далее. При этом важно помнить, что каждая новая стрелочка добавит взрывной рост не самого числа, а описания высоты степенной башни, которая используется для записи этого числа. Поэтому откинемся на спинку кресла и продолжим.

Есть куб, все вершины которого соединены отрезками красного или синего цвета. Цвета отрезков нужно подобрать так, чтобы не получилось, что 4 вершины, лежащие в одной плоскости, соединены отрезками одного цвета (см. картинку ниже, нижняя фигура — это то, чего в результате комбинирования цветов отрезков получиться не должно).

Для обычного 3-мерного куба задача решается, если и не в уме, то на бумаге геометрическим построением. Для 4-мерного куба уже нужно применить комбинаторику. Для 5-мерного и 6-мерного тоже. И так далее до 13-мерного куба: это нижняя граница измерений куба для которой доказано, что подобную комбинацию цветов отрезков соединяющих вершины подобрать можно, хотя сам Грэм запоролся уже на 7-мерном. А как быть с верхней границей? Грэм в своё доказал, что задача разрешима между 6 и неким большим числом. То есть в этом диапазоне измерений куба обязательно найдётся такой, где покрасить отрезки так, чтобы условие задачи выполнилось, будет невозможно. То самое «некое большое число» и было названо числом Грэма. И значение его G = g₆₄ = 3 ↑ g₆₃ 3.

Занавес! Хотя, а вдруг можно больше? Нет, не в смысле, G + 1 или G ↑ G G, а так чтобы число можно было бы реально для чего-нибудь применить? И такие числа есть. Причём, они уделывают G так же, как в своё время какое-то ссаное g₁ уделало гуголплекс в самом начале вычислений.

Собственно, вся проблема осталась только в способах записи. От степенных башен был переход к нотации Кнута, которая позволила хотя бы описать число Грэма. Потом случились цепочки Конвея, массивные и матричные нотации и вот это вот всё, что позволяет описать сколь угодно большое число, когда для предыдущего способа записи вставала проблема количества условных стрелочек. Не буду их тут описывать, во всяком случае сейчас. Всё-таки, напоминаю, что серия статей о больших числах носит информационно-развлекательный характер, и не хочется превращать её во всякое.

В итоге, вся эта дичь дошла до числа Райо. Это уже чистая философия, полученная на каком-то математическом конкурсе на запись самого большого числа на ограниченном пространстве доски, без использования бесконечности и всяких фокусов типа «самое большое число плюс один». В итоге, получилось, что число Райо — это самое маленькое число, большее, чем любое конечное число, определённое на языке теории множеств, с использованием гугол символов или меньше. Если вы поняли хоть что-то о порядке этого числа, вернее, нижней границы чисел Райо, то вы либо профессиональный математик, и не очень понятно, зачем вы дочитали до этого места, либо, как и я, врёте о том, что хоть что-то поняли.

А вот теперь держитесь, хорошего вам настроения и всего доброго. В следующей серии мы выйдем за пределы бесконечности, а там будет всё ещё добрее и веселее, хотя и несколько проще для понимания, чем то же число Райо. Или нет.

Источник

Степенная башня как считать

По принципу «чтоб добро не пропадало», предлагаю задачку, которая на днях случайно возникла и решилась в одном блоге при обсуждении некоего старого олимпиадного задания по математике (чур не гуглить, хоть я и не уверен, что соответствующий диалог можно раскопать гуглом). Задача связана со степенными башнями (тетрациями), поэтому я предваряю вопрос небольшим введением в степенные башни для тех, кто с ними не знаком.

Рассмотрим тетрацию 2012 2. Это невообразимо огромное число. По сравнению с ним, например, количество нейтронов, которые могли бы уместиться в видимой части Вселенной, есть просто незаметная кроха под ногами, почти точный нуль (хоть бы мы и упаковали нейтроны очень плотно, как в нейтронной звезде). Соответственно, невозможно записать все десятичные цифры этой степенной башни — для их записи не хватило бы всего пространства нашего мира, даже если бы нашелся способ выяснить все эти цифры за разумное время (что, впрочем, тоже невозможно). Но я и не собираюсь просить о невозможном.

Задача. Укажите три младшие десятичные цифры степенной башни 2012 2.

Просьба сдавать ответ в формате «. xxx», например, «. 123»; доказательства и вычисления пока оставим за кадром (но если вы сопроводите свой ответ кратким пояснением, то я его с интересом прочитаю). Не буду возражать против рекламы этой задачки среди потенциально заинтересованной аудитории. Время на решение пока не ограничивается. Ответы принимаются, комментарии скрыты. Для зачета нужно правильно и в надлежащем порядке указать все три цифры.

UPD: продолжение темы см. у fiviol а.

А вот сотенный разряд у меня получился не такой, как у Вас, причем до Вашего решения третью цифру мне сравнить было не с кем. Поскольку наши ответы в третьей цифре расходятся, я прошу Вас проверить свое вычисление. Если Вы уверены и подтвердите свой ответ, то тогда я перепроверю свой. Одно и то же число не может оканчиваться по-разному! 🙂

Источник