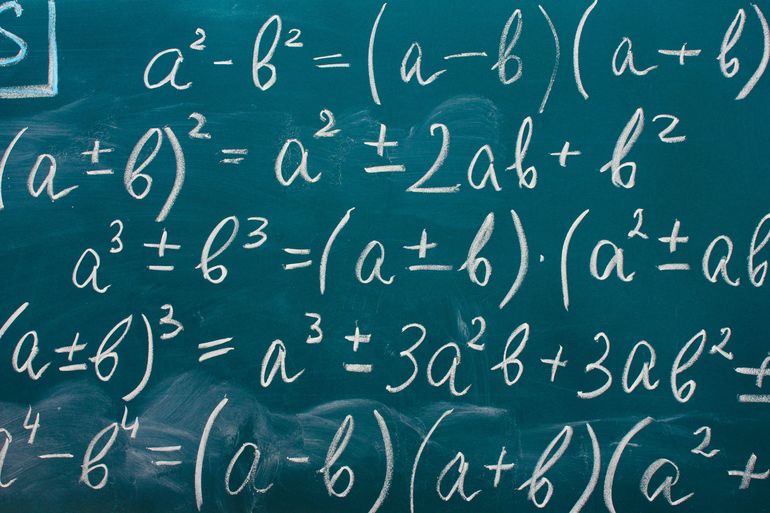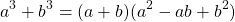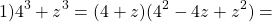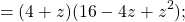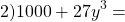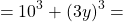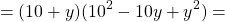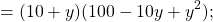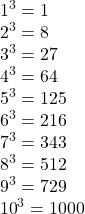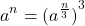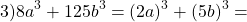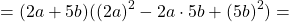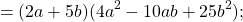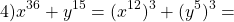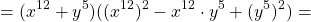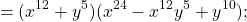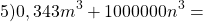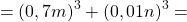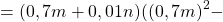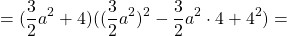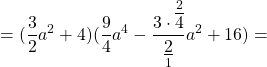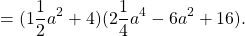Сумма кубов как вывести
Как использовать сумму кубов
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.
Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.
Вспомним, как выглядит формула суммы кубов.
a 3 + b 3 = (a + b)(a 2 − ab + b 2 )
Формула суммы кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.
(a + b)(a 2 − ab + b 2 ) = a 3 + b 3
Как разложить на множители сумму кубов
Рассмотрим пример. Необходимо разложить на множители сумму кубов.
Обратим внимание, что « 8x 3 » — это « (2x) 3 », значит, для формулы суммы кубов вместо « a » мы используем « 2x ».
Используем формулу суммы кубов. Только вместо « a 3 » у нас будет « 8x 3 », а вместо « b 3 » будет « 27y 3 ».
Применение суммы кубов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов в сумму кубов, используя формулу сокращенного умножения.
Обратите внимание, что произведение многочленов « (p + 1)(p 2 − p + 1) » напоминает правую часть формулы суммы кубов « a 3 + b 3 = (a + b)(a 2 − ab + b 2 ) », только вместо « a » стоит « p », а на месте « b » стоит « 1 ».
Используем для произведения многочленов « (p + 1)(p 2 − p + 1) » формулу сумму кубов в обратную сторону.
Рассмотрим пример сложнее. Требуется упростить произведение многочленов.
В этом произведении многочленов не так очевидно, что будет являться в формуле « a », а что « b ».
Теперь представим скобку « (4a 2 − 6a + 9) » таким образом, чтобы она соответствовала правой части формулы суммы кубов.
Используем формулу суммы кубов и решим пример до конца.
Алгебра. 7 класс
Конспект урока
Сумма кубов. Разность кубов
Перечень вопросов, рассматриваемых в теме:
Формулы сокращённого умножения.
(a + b) 2 = a 2 + 2ab + b 2
(a – b) 2 = a 2 – 2ab + b 2
a 3 + b 3 = (a + b)(a 2 – ab + b 2 )
a 3 – b 3 = (a – b)(a 2 + ab + b 2 )
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Формула суммы кубов.
Применив правило умножения многочленов, и приведя подобные члены, получим:
(a + b)(a 2 – ab + b 2 ) = a 3 – a 2 b + ab 2 + ba 2 – ab 2 +b 3 = a 3 + b 3
a 3 + b 3 = (a + b)(a 2 – ab + b 2 )
Равенство называют формулой суммы кубов.
Читается так: «сумма кубов двух чисел равна произведению суммы этих чисел и неполного квадрата их разности».
Формула разности кубов.
Аналогично докажем формулу разности кубов.
(a – b)(a 2 + ab + b 2 ) = a 3 + a 2 b + ab 2 – ba 2 – ab 2 – b 3 = a 3 – b 3
Читается так: «разность кубов двух чисел равна произведению разности этих чисел и неполного квадрата их суммы».
Выражения (a 2 + ab + b 2 ) и (a 2 – ab + b 2 ) называют неполным квадратом суммы или разности.
Формула задаёт разложение многочленов:
a 3 + b 3 и a 3 – b 3 на два множителя:
(a + b)(a 2 – a b+ b 2 ) и (a – b)(a 2 + ab + b 2 ).
Формулы суммы и разности кубов используют для упрощения вычислений.
Разбор решения заданий тренировочного модуля.
Выполните умножение многочленов:
Разложите многочлен на множители:
(x +2)(x 2 – 2x +4) – x(x–3)(x+3).
x 3 + 2 3 – x(x 2 – 9) = x 3 + 8 – x 3 + 9x = 8 + 9x.
Доказать, что выражение 123 3 + 27 3 кратно 50.
a 3 + b 3 = (a + b)(a 2 – ab + b 2 ),
получим: (123 + 27)(123 2 –123 · 27 + 27 2 ) =150 · (123 2 –123 · 27 + 27 2 ).
Произведение делится на 50, так как первый множитель делится на 50: (150 : 50 = 3). Нет необходимости считать значение выражения в скобках. Утверждение доказано.
Краткое описание
В алгебре большим спросом пользуются различные формулы и соответствующие правила сокращённого умножения. При правильном подходе ученик может максимально быстро и правильно решать большие уравнения. Универсальные формулы были получены специалистами для умножения и вычитания сразу нескольких многочленов. Только подготовленные ученики могут максимально быстро решать поставленные задачи, существенно упростив используемое выражение. Базовые правила востребованных преобразований позволяют выполнять определённые манипуляции с уравнениями.
Если максимально придерживаться основных рекомендаций, то можно будет получить в левой части примера равенство выражения, расположенное с правой стороны. Ученик должен хорошо владеть теми формулами, которые применяются для сокращённого умножения, используемого во время решения задач, а также уравнений. Но даже в этом случае нужно соблюдать ряд нюансов, чтобы можно было избежать допущения грубых ошибок.
Интересным фактом является то, что некоторые формулы для быстрого умножения были выведены экспертами ещё в конце четвёртого тысячелетия до нашей эры. Именно целеустремлённые греки максимально развили идеи своих предшественников, из-за чего им удалось разработать сразу несколько важных и полезных правил. Но в те времена математики мыслили совершенно иначе, так как они стремились воссоздать числа с помощью подручных материалов или геометрических фигур. К примеру: специально обтёсанные камни на счётной доске из дерева.
Ещё несколько лет назад формулы для определения суммы различных величин выводились исключительно геометрическим методом. Эксперты практиковали рассечение квадрата на разные фрагменты. Настоящий подъём науки пришёлся на времена Ньютона и других учёных. Именно эти целеустремлённые люди смогли внести огромный вклад в развитие формул для алгебры, представив обществу усовершенствованный вариант.
Сумма и разность кубов
Для изучения этой темы должно быть отведено достаточно времени, так как только после изучения всех нюансов ученик сможет должным образом применить свои знания. Основная формула суммы кубов двух чисел выглядит следующим способом: w3 + y3 = (w + y) (w2 — wy + y2). Стоит отметить, что задействованное выражение w2 — wy + y2 отличается от правой части только присутствующим коэффициентом при y. Именно поэтому такое выражение называют неполным квадратом разности.
Обязательно нужно усвоить правило, что итог двух кубических (ударение падает на слог с первой буквой «и») корней будет соответствовать произведению суммы этих выражений на неполный квадрат их разности. Нужно понимать, что каждая математическая задача обладает определёнными характеристиками, которые нельзя оставить без внимания.
Элементарную формулу сумму кубов получают следующим образом:
Зафиксированная сумма кубов раскладывается по специальной технологии, так как разность кубов двух уравнений равна произведению разности этих уравнений на неполный квадрат их суммы. В качестве примера можно изучить следующую задачу:
По описанному примеру можно понять, что решать поставленные задачи можно быстро и без ошибок, но это только в том случае, если заранее изучить все правила. Ученику необходимо решить минимум три задачи, чтобы увидеть разницу между уравнениями и выполнить полное раскрытие темы.
Основное доказательство ФСУ
Во время изучения математики перед учениками неизбежно возникает необходимость определить сумму кубов. Примеры решения элементарных и более сложных задач позволяют лучше усвоить тему. Основное доказательство ФСУ отличается своей простотой и элементарностью. Базируясь на свойствах умножения можно правильно выполнять сложение цифр из всех частей формул в скобках. В качестве примера можно рассмотреть формулу квадрата разности: d — r2= d−2dr + r2.
Чтобы иметь возможность возвести пример во вторую степень, необходимо задействованное выражение умножать само на себя:
После этого можно считать, что формула полностью доказана. Все остальные ФСУ описываются подобным образом.
Основная цель применения математических приёмов — максимально быстрое и правильное умножение, а также возведение в степень имеющихся выражений. Но это далеко не все способы использования ФСУ. Распространённые методы сокращённого умножения применяются для упрощения выражений, разложение задействованных многочленов на множители, а также для работы с различными дробями.
При правильном подходе ФСУ позволяет даже вычислить значения математических выражений. Главная задача — иметь достаточно навыков, чтобы заметить, где именно будет уместна формула. Если по условиям задачи нужно возвести в квадрат любое число (к примеру: 79), тогда вместо громоздких вычислений можно прибегнуть к более лаконичным и понятным записям: 79=80−1; 792=80−12=6400−160+1=6241.
Формулы умножения с упрощённой схемой и специальные таблицы позволяют гораздо быстрее выполнить все необходимые вычисления. Определённые сложности могут возникнуть с выделением квадрата двучлена, так как в этом случае можно допустить много ошибок.
Математическое выражение 4х2+4х-3 можно легко преобразовать. В этом случае можно получить следующий результат: 2х2 +2*2*х *1 +12−4=2х+12−4. Интересным является то, что именно такое преобразование активно используется в интегрировании.
Вспомогательная информация
Именно сумма сразу двух геометрических кубов получила большой спрос в алгебре для кардинального упрощения многочленов. Лучше всего рассматривать конкретные примеры, которые относятся к категории сложных уравнений. Без наставлений учителя решать такие задачи при помощи универсального тригонометрического аппарата будет крайне сложно, особенно для неподготовленного школьника.
Грубые ошибки допускают те, кто плохо знаком со свойствами синусов и косинусов. На помощь может прийти правило суммы двух кубов, так как все описанные примеры максимально повторяют разложение на отдельные множители выражения a 2 + b 2. Но в этом случае вместо а — sinx, а b заменил cosy.
Если следовать правилам, то многоуровневое тригонометрическое выражение может легко превратиться в лаконичную запись, где sin3x + cos3y. После этого остаётся применить эту универсальную формулу во время подсчёта. Многие люди практически на память знают все квадраты к используемым в повседневной жизни натуральным числам до пятнадцати. А ученики, которые занимаются арифметикой на постоянной основе, владеют большим количеством квадратов. Гораздо сложнее работать с кубами. Если по условиям задачи нужно посчитать сумму двух таких кубов, то гораздо практичнее и быстрее применить формулу разложения на отдельные множители.
На просторах интернета много различных программ, которые считают сумму двух кубов с различными иллюстрациями промежуточных вкладов. Эта разработка программистов пригодится школьникам, стремящимися проверить результаты выполненных работ, а также взрослым, которые хотят возобновить в памяти школьный курс алгебры.
Особенности использования уравнений
Для лучшего усвоения этой темы следует более подробно изучать приведённые примеры. В качестве основы следует взять элементарную формулу для квадрата суммы двух чисел: h+ hl = h2+2 hl + l2. Этот математический пример необходимо читать только таким образом: квадрат суммы для двух выражений h и l соответствует квадрату первого выражения, удвоенного произведения уравнения, а также квадрату второго выражения. Точно таким образом математики читаются все остальные формулы.
Если нужно записать квадрат разности h — l2= h2−2hl + l2. Запись такого уравнения выглядит только так: квадрат математической разности двух примеров максимально соответствует конечной сумме, которая была получена от квадрата этих утверждений. Но также перед учеником может возникнуть необходимость правильно прочитать более сложную формулу: h + l3= h3+3h2l +3hl 2+ l3. Задействованный куб суммы двух математических уравнений соответствует итоговым данным этого примера. В этом уравнении присутствует утроенное произведение квадрата первого выражения на второе.
Ключевые нюансы
Если есть необходимость самостоятельно вычислить куб суммы двух слагаемых, тогда первым делом определяют сумму, которая включает в себя куб первого слагаемого, утроенного произведения квадрата первого и второго слагаемого. В алгебре это выражение выглядит так: (d+e) 3 = d 3 +3 d 2 e +3 de 2 + e 3.
Специальные формулы сокращённого умножения являются неотъемлемой темой в школьной программе по алгебре, так как она обязательно пригодится во время решения многоуровневых задач. Это своеобразная основа, на которой строятся решения интегральных исчислений. Онлайн-калькуляторы помогают лучше освоить технологию применения формулы двух кубов, которые можно свернуть, а потом снова открыть для приведения уравнения в нужный вид.
Сумма кубов: формула, примеры
Формула суммы кубов
Сумма кубов двух выражений представляет собой сумму данных выражений, умноженную на неполный квадрат их разности.
Формула будет записана, таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Геометрический смысл формулы суммы кубов
В качестве примера можно рассмотреть куб. Пусть каждая из его сторон равна:
В противоположные углы данной фигуры можно вписать еще кубы, стороны которых равны a и b.
Расчет объемов этих кубов будет выглядеть следующим образом:
Объем одной из фигур можно вычислить по формуле:
\(V_ <1>= a(a+b)^2-V_a = a(a^2+2ab+b^2 )-a^3 = 2a^2 b+ab^2\)
Объем второй фигуры можно рассчитать, таким образом:
\(V_ <2>= b(a+b)^2-V_b = b(a^2+2ab+b^2 )-b^3 = a^2 b+2ab^2\)
Общий объем составит:
\((a+b)^3 = a^3+b^3+2a^2 b+ab^2+a^2 b+2ab^2\)
\(a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) = (a+b)(a^2-ab+b^2 )\)
В итоге удалось записать формулу куба суммы.
Как раскладывается формула суммы кубов
Следует записать уравнение куба суммы:
С помощью рассматриваемой формулы достаточно просто определить сумму двух кубов:
\(a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) = (a+b)(a^2-ab+b^2 )\)
Следует отметить, что записанное выражение представляет собой неполный квадрат разности:
Полным квадрат разности будет записан, следующим образом:
По результатам преобразований получаем уравнение, с помощью которого можно разложить сумму пары кубов на множители:
Примеры использования формул
Даны уравнения: \(x^3+y^3\)
Каждое из записанных выражений требуется разложить на множители.
Выполним необходимые преобразования:
\(125-64y^3 = 5^3-(4y)^3 = (5-4y)(25+20y+16y^2 )\)
Сумма кубов
В алгебре формулы сокращенного умножения — тождества, то есть любая из формул верна как для перехода от правой части к левой, так и от левой к правой.
Мы выяснили, что произведение суммы двух выражений и неполного квадрата разности равно сумме кубов этих выражений. И обратно,
сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Формула суммы кубов:
С помощью схемы сумму кубов можно представить так:
На практике, чтобы пользоваться формулой суммы кубов, ее надо научиться видеть.
сначала надо увидеть, что 1000 — это куб 10, а 27y³ — куб (3y):
и только потом расписать его как сумму кубов:
На первом этапе изучения формулы можно использовать схему.
Таблица кубов от 1 до 10 поможет нам увидеть кубы чисел:
Свойство степеней поможет определить куб степени:
Рассмотрим еще примеры разложения по формуле суммы кубов.
Чтобы определить, сколько цифр после запятой нужно записать в десятичной дроби, если известен ее куб, надо количество знаков после запятой в кубе числа разделить на 3:
В алгебре формулу суммы кубов чаще всего используют для упрощения действия разложения многочленов на множители.