Таблица истинности как решать

Таблица истинности как решать

2) Логическое сложение или дизъюнкция:

Таблица истинности для дизъюнкции

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

3) Логическое отрицание или инверсия:

Таблица истинности для инверсии

A	¬ А
1	0
0	1

4) Логическое следование или импликация:

«A → B» истинно, если из А может следовать B.

Обозначение: F = A → B.

Таблица истинности для импликации

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

5) Логическая равнозначность или эквивалентность:

Источник

Логические выражения и таблица истинности

Логические выражения и таблица истинности

Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.

Логическое выражение — составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения таблицы истинности:

1. подсчитать количество переменных n в логическом выражении;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов: число переменных + число операций;

6. выписать наборы входных переменных;

7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

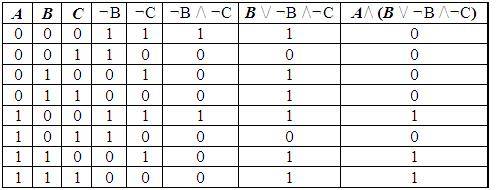
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.

Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.

1. В выражении две переменные А и В (n=2).

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).

5. К_{столбцов}=n+5=2+5=7 столбцов.

Источник

Разбор 2 задания ЕГЭ по информатике

Объяснение задания 2 ЕГЭ по информатике

2-е задание: «Таблицы истинности»
Уровень сложности — базовый,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.

Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы

«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»

Таблицы истинности и порядок выполнения логических операций

Таблица истинности операции НЕ

Таблица истинности операции И (конъюнкция)

Таблица истинности операции ИЛИ (дизъюнкция)

Таблица истинности операции Импликация (если…, то…)

Таблица истинности операции Эквивалентность (тогда и только тогда, …)

О преобразованиях логических операций читайте здесь.

Решение заданий 2 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Логическая функция F задается выражением

(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Перем.1	Перем.2	Перем.3	Перем.4	F
.	.	.	.	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

print(‘x y z w’) for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)

Язык pascalAbc.net:

begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.

Ответ:

Результат: xwzy

🎦 Видео решения 169 задания К.Полякова (бескомпьютерный вариант):

Миша заполнял таблицу истинности функции:

(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)

но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:

Перем.1	Перем.2	Перем.3	Перем.4	F
.	.	.	.	F
1	1	0
1	0	0
1	1	0	0

Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.

Результат: ywxz

✎ Способ 2. Программирование:

begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) false = 0, True = 1

Сопоставив их с исходной таблицей, получим результат: ywxz

print (‘x y z w’) for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y)) F=0 :

Сопоставив их с исходной таблицей, получим результат:

Результат: ywxz

🎦 Доступно видео решения этого задания (бескомпьютерный вариант):

🎦 Видео (решение 2 ЕГЭ в Excel):

Логическая функция F задается выражением

¬a ∧ b ∧ (c ∨ ¬d)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

Перем.1	Перем.2	Перем.3	Перем.4	F
.	.	.	.	F
0	1	0	0	1
1	1	0	0	1
1	1	0	1	1

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

Результат: cbad

🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:

Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
.	.	.	.	F
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

✍ Решение:

Результат: xzwy

✎ Способ 2. Программирование:
Язык pascalABC.NET:

begin writeln(‘x ‘,’y ‘,’z ‘,’w ‘); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.

🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

Логическая функция F задаётся выражением

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.

Перем.1	Перем.2	Перем.3	Перем.4	F
.	.	.	.	F
0	0	0
0	1	0	1	0
1	0	0

Результат: xwzy

🎦 Видеорешение (бескомпьютерный вариант):

Задания для тренировки

Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.

Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?

✍ Решение:

Результат: 31

Подробное объяснение данного задания смотрите на видео:

Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.

Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?

✍ Решение:

Результат: 8

Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.

Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?

✍ Решение:

Результат: 256

Дан фрагмент таблицы истинности выражения F.

x1	x2	x3	x4	x5	x6	x7	F
1	0	0	1	1	1	1	0
0	1	0	0	1	0	1	1
0	1	0	1	1	0	1	0

Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7

✍ Решение:

Результат: 1

Решение 2 задания ГВЭ по информатике смотрите на видео:

Дано логическое выражение, зависящее от 5 логических переменных:

(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)

Сколько существует различных наборов значений переменных, при которых выражение истинно?

✍ Решение:

Теперь рассмотрим каждый случай отдельно:

¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.

Результат: 2

Подробное решение задания смотрите в видеоуроке:

Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	x6	F
0	0	1	1	0	0	1
0	0	0	0	1	1	1
1	0	1	0	1	1	1
0	1	1	1	0	1	0

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.

✍ Решение:

Результат: 62

Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	x6	x7	F
0	0	0
0	0	1
1	1	1

Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7

✍ Решение:

Результат: 4

В видеоуроке рассмотрено подробное решение 2 задания:

Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

№	Перем. 1	Перем. 2	Перем. 3	F
.	.	.	F
1	0	0	0	0
2	0	0	1	0
3	0	1	0	1
4	0	1	1	1
5	1	0	0	0
6	1	0	1	0
7	1	1	0	0
8	1	1	1	1

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

Результат: yzx

Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:

Источник

Таблица истинности

Что такое таблицы истинности

Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).

Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.

Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.

Логические операции

Логические операции — построение из одного или нескольких высказываний нового высказывания.

Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.

К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.

Логические выражения

Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».

Их можно разделить на два типа:

Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.

Унарной в данном случае называется операция, которая используется относительно одной величины.

Конъюнкция

Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧.

Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.

Дизъюнкция

Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.

Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.

Правила составления таблицы истинности

Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.

Строить таблицы истинности необходимо по следующему алгоритму:

Примеры построения таблицы истинности

Задача

Решение

А	В	\(А \vee В\)	¬А	¬В	\(¬А \vee ¬В\)	\((A \vee B) \wedge (¬A \vee ¬B)\)
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

После заполнения таблицы, ответ будет выглядеть следующим образом:

F = 0 при A = B = 0 и A = B = 1

Задача

Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)

Решение

X	Y	Z	¬ Z	\(Y \wedge ¬Z\)	\(X \vee Y \wedge ¬Z\)
0	0	0	q	0	0
0	0	1	0	0	0
0	1	0	1	1	1
1	0	0	1	0	1
1	0	1	0	0	1
1	1	0	1	1	1
1	1	1	0	0	1

После заполнения таблицы, ответ будет выглядеть следующим образом:

F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1.

Источник